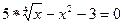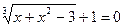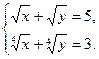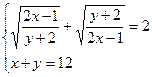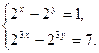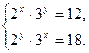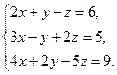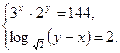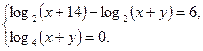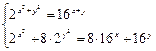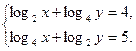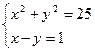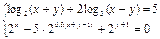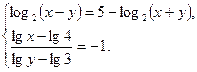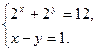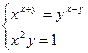Символьное решение систем уравнений

 

Функция

solve,x1,х2...х3

позволяет найти значение перечисленных переменных, при которых содержащее их выражение становится равным нулю. Для решения системы уравнений в шаблон функции solve вставляется вектор, длина которого равна количеству уравнений в системе. Уравнения записываются в вектор.

На рис. 68 приведен пример применения функции solve для решения систем уравнений.

 

Рис.68. Пример применения функции solve для решения систем уравнений.

Оборудование, инструменты и приборы

ПЭВМ, система MathCad

Варианты заданий

Варианты заданий приведены в таблицах 4.12 -4.15.

Задание 1

Решить уравнение согласно заданию своего варианта. Найти все корни уравнения. Точность решения 0.0001. Варианты заданий приведены в табл.4.12.

 

Таблица 4.12

Варианты заданий

 

№ вар	Задание	№ вар	Задание	№ вар	Задание
	1/2*x^2+3*cos(x)– 5=0				2*x^2+ln(2*x–x^2) =0
			ln(2*x–x^3)+2=0		4*x^2–5*x^-1–2=0
	sin(x)–5*x^3+1=0				x^3–8*x^2+1.5=0
	|x|–3*x^2+1=0		4*|sin(x)|+x^2–4=0		4*cos(x)+x^2–4=0
			7*|sin(x)|–x–5=0		1/2*x^3+3*cos(x)+2=0
	1/2*x+3*cos(x)+2=0		2*x^5–8*x^2+0.8=0		8*x^3+5*x^2–17*x^-1=0
	8*x^2+5*x^-1–17=0		5*x^2+3*cos(x)–4=0		8*x^3+ ln(x^2) =0
	5*x^3–6*x+0.2=0		3–7*cos^2(x)*sin(x)– –3* sin^3(x)=0		ln(7*x)–x^-1=0
	5*x^4–6*x^2+0.5=0		8*sin(2x)– 3*cos^2(x)–4=0		1/4*x^4–3*cos(x)+2=0
	5*x^3–6*x^2+3=0		x^2+ sin(x)–5*x^3=0		2*x^4+x^3–3*sin(x)=0

 

Задание 2

Решить уравнение полиномиального вида, заданного функцией F(x):= A0+A1*x+A2*x²+A3*x³. Значения коэффициентов взять в соответствии со своим вариантом. Варианты заданий приведены в табл.4.13.

Таблица 4.13

Варианты заданий

№ вар.	Значения коэффициентов
А0	А1	А2	А3
	-5
	-55
		-8	-10
	-3	-11
	-5		-9
	-52		-6
		-33
	-4
	-12
	-7
			-11
	-7		-9
	-3
			-12
			-2
		-5		-11
			-2
			-5
	-4
	-6		-2
				-9

 

 

Задание 3

Решить систему линейных алгебраических уравнений матричным методом. Варианты заданий приведены в табл. 4.14.

Таблица 4.14

Варианты заданий

 

№ вар	Задание	№ вар	Задание	№ вар	Задание
	5x1+3x2-4x3+x4=8 -3x1+8x2-4x3-2x4=-5 x1-12x2+2x3-2x4=-3 -3x1+7x2+x3-4x4=-6		0.5x+0,5x2-4x3+x4=8.5 3x1-8x2-4x3-x4=-12 6x1-7x2+2x3-2x4=-5 -3x1+7x2+5x3-4x4=11		-x1+2x2+2x3+8x4=10 -9x1+x2+3x3-7x4=0 11x1+5x2-2x3+5x4=7 x1+3x2+5x3-6x4=4
	9x1+5x2-4x3+x4=6 -x1+6x2-3x3-5x4=-2 x1-2x2+2x3-2x4=-3 -5x1+3x2+x3-x4=-1		2x1-6x3+x4=3 11x1+8x2-x3-2x4=16 x1-2x2+2x3-4x4=0 -4x1+x3-4x4=-10		-4x1-5x2+4x3-5x4=-11 x1-x2-2x3+8x4=7 -4x1+7x2-4x3-4x4=9 9x1+4x2-2x3-12x4=3
	-5x1+4x2-4x3-x4=-4 -x1+6x2-3x3-5x4=-2 x1-3x2+5x3+6x4=7 -4x1+x2+x3-4x4=-2		15x1+13x2-4x3+x4=20 5x1+8x2-4x3=5 3x1-x2+3x3-2x4=-3 -x1+4x2+x3-4x4=0		-10x1-9x2+x3+2x4=-2 4x1+5x2+4x3+12x4=6 -8x1-2x2-x3+9x4=15 4x1-3x2-3x3-2x4=-3
	x1+8x+4x3-2x4=7 7x1-x2+x3-9x4=10 6x1-3x2+x3+12x4=4 11x1-9x2-5x3+6x4=0		10x1+4x3+x4=18 9x1+8x2-4x3-11x4=0 x1-12x2+2x3-2x4=-5 x1+7x2+x3-x4=6		-2x1-6x2+5x3+9x4=-9 6x1+8x2-4x3-2x4=-5 -3x1-4x2-8x3+7x4=13 x1+2x2-7x3+9x4=-4
	-2x1+2x2-9x3+5x4=6 x1-2x2+10x3-7x4=-4 -11x1+x2+9x3-2x4=1 3x1+7x2-x3-x4=3		4x1+x2-4x3+x4=8 -3x1+8x2-4x3-2x4=-5 x1+4x2+2x3-2x4=7 -1.5x1+3x2+x3-4x4=-6		-8x1+2x2+x3-x4=0 x1+10x2-6x3+x4=-10 5x1-2x2+9x3-4x4=-8 -7x1-7x2-5x3+3x4=2
	-x1-5x2-6x3+7x4=0 3x1-7x2-2x3-2x4=-2 2x1+10x2+4x3+2x4=5 -13x1-x2-8x3-3x4=-1		5x1+3x2-4x3+x4=8 x1+x2-4x3-5x4=3 5x1-2x2+4x3-2x4=-3 -x1+7x2-4x4=0		-8x1+2x2+x3-x4=0 x1+10x2-6x3+x4=-10 5x1-2x2+9x3-4x4=-8 -7x1-7x2-5x3+3x4=2
	-5x1+3x2-x3+5x4=-2 7x1-6x2-7x3+x4=3 x1+x2-11x3-5x4=9 5x1-14x2+4x3-6x4=7		5x1+3x2-4x3+x4=8 -3x1+6x2-4x3=-7 x1-9x2+2x3+4x4=0 3x1-2x2+2x3-2x4=-7		6x1-4x2+3x3+5x4=-2 -4x1+7x2-5x3-4x4=-4 2x1-2x2+6x3-72x4=-4 -2x1+7x2+x3-5x4=-3

 

 

Окончание табл. 4.14

	10x1+6x2-8x3+2x4=4 6x1-4x2+8x3+4x4=10 -2x1+6x2-4x3+4x4=6 6x1-15x2-2x3+8x4=3		7x1-6x2-7x3+x4=3 x1-6x2+2x3-2x4=-1 -3x1+7x2+x3-4x4=-6 2x1+10x2+4x3+2x4=5		3х1+2x2-9x3+2x4=0 6x1+9x2-5x3-x4=-3 3x1-4х2+x3-7x4=-5 2x1+7x2+2x3-3x4=-6
	2.5x1+3x2-4x3+x4=0 -3x1+8x2-2x4=-3 3x1-2x2+2x3-2x4=-7 -3x1+7x2+x3-4x4=-2		-3x2-x3+x4=-3 -x1+5x2+2x3-2x4=-5 x1-2x2+6x3-2x4=2 -3x1+x2+x3-4x4=-8		5x1+2x2-x3+3x4=7 -7x1+6x2-5x3-7x4=-5 x1-12x2+2x3-2x4=-3 -4x1+7x2+x3-7x4=-6
	x1+3x2+4x3+x4=8 -3x1+2x2-4x3-2x4=-5 x1-6x2+2x3-2x4=-1 -3x1+7x2+x3+4x4=12		x1+3x2+2x3+x4=4 -3x1+x2-4x3-2x4=-5 x1-5x2+2x3+3x4=9 -3x1+4x2+x3-7x4=-5		1. 4x1+x2-6x3+x4=5 4x1+8x2-2x3-3x4=-5 -x1-12x2+3x3-2x4=-3 -5x1+7x2+3x3-3x4=-6

 

 

Задание 4

Решить систему линейных алгебраических уравнений из предыдущего задания при помощи функции lsolve.

 

Задание 5

Решить систему уравнений двумя способами (с использованием функции find и с использованием стандартной функции minerr. Варианты заданий приведены в табл.4.15.

Таблица 4.15

Варианты заданий

№ вар	Задание	№ вар	Задание	№ вар	Задание

Окончание табл. 4.15

 

Порядок выполнения работы.

3. Создать MathCad – документ и сохранить его под именем «Решение_уравнений».

4. Выполнить задания 1 – 5 в соответствии с данными своего варианта.

Содержание отчета.

 

Отчет должен содержать:

· номер, название и цель работы;

краткую теоретическую часть, включающую описание методов решения уравнений и систем уравнений;

· результаты выполнения работы согласно заданию, выданному преподавателем, а именно, в отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “ Решение_уравнений ”;

· заключение по работе.

 

 

Контрольные вопросы

1. Решение уравнений при помощи функции root.

2. Решение уравнений при помощи функции polyroot.

3. Символьное решение уравнений.

4. Решение систем нелинейных уравнений при помощи функции find.

5. Решение систем нелинейных уравнений при помощи функции minerr.

6. Символьное решение систем уравнений.

7. Решить уравнение по заданию преподавателя.

8. Решить систему уравнений по заданию преподавателя.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 24

Решение дифференциальных уравнений и систем

Цель работы: научиться решать дифференциальные уравнения и системы дифференциальных уравнений.

.

Теоретическая часть