
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное интегрирование жестких систем обыкновенных дифференциальных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Жесткие системы можно сравнить с плохо обусловленными системами алгебраических уравнений. Рассмотрим систему дифференциальных уравнений(ДУ)
где
где n= m, m+ 1, m+ 2,…. Устойчивость и сходимость методов (6.22) определяется расположением корней характеристического уравнения, т.е. | q |£1 - корни принадлежат единичной окружности. Среди методов (6.22) выделим те, которые позволяют получить асимптотически устойчивые решения. Пример. В качестве частного случая (6.21) рассмотрим уравнение вида
где:
что означает устойчивость решения. Рассмотрим для задачи (6.23) метод Эйлера
где: n =0, 1, 2, …, Оценка (6.24) для метода Эйлера будет выполнена тогда и только тогда, когда |q|£1. Шаг t лежит в интервале 0 < t <2/½l½. Метод Эйлера для задачи (6.23) устойчив при выполнении этого условия.
Определение 1. Разностный метод (6.22) называется абсолютно устойчивым, если он устойчив при любом t >0. Определение 2. Разностный метод называется условно-устойчивым, если он устойчив при некоторых ограничениях на t. Например, метод Эйлера для (6.23) условно-устойчив, т.к. 0 < t <2/½l½. Примером абсолютно устойчивого метода является неявный метод Эйлера
Замечание. Условная устойчивость является недостатком явных методов в связи с тем, что приходится выбирать мелкий шаг интегрирования. Пример для задачи (6.23). Если l=-200, тогда t£0.01. Если мы рассмотрим интервал (0,1], то необходимо будет 100 шагов. Неявные методы со своей стороны приводят к решению на каждом шаге нелинейного уравнения, но это уже недостаток неявного метода.
6.3.1 Понятие жесткой системы ОДУ
Замечание. Все вышерассмотренные методы легко реализуются на примере одного уравнения и легко переносятся на системы ДУ, но при решении систем возникают дополнительные трудности, связанные с разномасштабностью описанных процессов. Рассмотрим пример системы двух уравнений:
где: t >0; a1,a2>0. Это система однородных независимых ДУ
Решение монотонно убывает с ростом t. Пусть коэффициент а2 на порядок и выше больше а1, т.е. а2>>a1. Тогда компонента u2 затухает гораздо быстрее u1, начиная с некоторого момента времени t и тогда решение задачи u(t) полностью будет определяться поведением компоненты u1. Однако при численном решении данной задачи шаг интегрирования t будет определяться компонентой u2, несущественной с точки зрения поведения решения системы. Рассмотрим метод Эйлера для решения данной системы
Он будет устойчив, если на t наложены ограничения
Учитывая, что
Такие трудности могут возникнуть при решении любых систем ОДУ. Рассмотрим в качестве примера систему
где А -квадратная матрица m*m. Если матрица А имеет большой разброс собственных чисел, то возникают проблемы с разномасштабностью описываемых системой процессов. Допустим, что матрица А постоянна (т.е. не зависит от t). Тогда система (6.21) будет называться жесткой, если: 1) вещественные части собственных чисел 2) число Если же матрица А зависит от t, то и собственные числа зависят от t и Решение жесткой системы (6.25) содержит как быстроубывающие, так и медленно убывающие составляющие.
6.3.2 Некоторые сведения о других методах решения жестких систем
Разностные методы (6.22) для решения жестких систем на практике используются в виде методов Гира (неявный разностный метод) и метода матричной экспоненты(метод Ракитского).
6.3.2.1 Методы Гира
Это частный случай методов (6.22), когда коэффициент
где l =2,..., p. Решив систему линейных уравнений (6.26) с учетом предыдущих условий, получаем все нужные коэффициенты. Трехшаговый метод Гира (частный случай методов (6.22) с учетом условий (6.26)) имеет вид
При m =4, получаем четырехшаговый метод Гира
Запишем систему (6.26) в виде
Решив (6.29) для каждого случая можем найти коэффициенты
6.3.2.2 Метод Ракитского(матричной экспоненты) решения систем ОДУ
где: Допустим, что матрица А - постоянная, т.е. ее элементы не зависят от времени. Система (6.30)–однородная, с постоянными коэффициентами. Запишем аналитическое решение (6.30)
где
Пусть необходимо (6.30) проинтегрировать при значениях t = t, 2 t, 3 t,…. Если точно знать матрицу
……………..…
Таким образом, задача сводится к тому, чтобы достаточно точно знать матрицу
Каждый столбец матрицы
где
Если эта матрица найдена, то решение находится по (6.31). Для исследования разностных методов при решении жестких систем рассматривают модельное уравнение
где l-произвольное комплексное число. Для того, чтобы уравнение (6.33) моделировало исходную систему (6.30) его нужно рассматривать при таких значениях l, которые являются собственными числами матрицы А. Многошаговые разностные методы (6.31) имеют вид
где: n=m, m +1…; m=t*l. Если решение уравнения (6.34) искать в виде
Для устойчивости метода достаточно выполнения условия корней Предварительные сведения. Областью устойчивости разностных методов называется множество всех точек комплексной плоскости m=t*l, для которых разностный метод применительно к уравнению (6.33) устойчив. Определение 1. Разностный метод называется А-устойчивым, если область его устойчивости содержит левую полуплоскость комплексной полуплоскости, т.е. Rem<0. Замечание. Решение модельного уравнения (6.33) асимптотически устойчиво при значениях Rem<0, поэтому сущность А-устойчивого метода заключается в том, что А-устойчивый разностный метод является абсолютно устойчивым, если устойчиво решение исходного дифференциального уравнения. Так как класс А-устойчивых методов узок, то пользуются А(a)-устойчивым методом. Определение 2. Разностный метод (6.31) называется А(a)-устойчивым, если область его устойчивости содержит угол меньший a, т.е. |arg(-m)|<a, где m=t*a. Исходя из этого определяется, что при a=90°=p/2 А(p/2) устойчивость совпадает с определением А-устойчивого метода.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.008 с.) |

 ,
,
 . Для решения (6.21) рассмотрим разностные методы вида
. Для решения (6.21) рассмотрим разностные методы вида ,
,
 ,
,
 ; l<0;
; l<0; 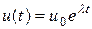 - решение ДУ. При l <0 решение есть монотонно убывающая функция при t®µ. Для этого решения можно записать при любом шаге t >0
- решение ДУ. При l <0 решение есть монотонно убывающая функция при t®µ. Для этого решения можно записать при любом шаге t >0 ,
,
 ,
, , q -промежуточный параметр, равный 1+tl.
, q -промежуточный параметр, равный 1+tl. ,
, .
. ,
, .
. .
. .
.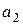 >>
>>  , получаем окончательное ограничение на t
, получаем окончательное ограничение на t .
. ,
,
 для всех k, где к =1,…,m;
для всех k, где к =1,…,m; велико (десятки и сотни), и число S называется числом жесткости системы.
велико (десятки и сотни), и число S называется числом жесткости системы. зависят от t.
зависят от t. ,
,  . Запишем числовые коэффициенты, которые определяются из условия p -го порядка точности аппроксимации системы разностными методами
. Запишем числовые коэффициенты, которые определяются из условия p -го порядка точности аппроксимации системы разностными методами ;
;  ;
; 
 .
.
 .
.
 .
.
 , к =1,2,…, т.
, к =1,2,…, т. ;
;  ; А -матрица размерности n*n.
; А -матрица размерности n*n.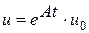 ,
,
 -матричная экспонента и
-матричная экспонента и +….
+….
 , то точное решение в указанных точках можно получить по формуле (6.31), т.е. решение можно записать
, то точное решение в указанных точках можно получить по формуле (6.31), т.е. решение можно записать
 .
. -
-  вычисляют по формуле
вычисляют по формуле ,
, - вектор столбец, в i - ой строке которого 1, а в остальных - нули.
- вектор столбец, в i - ой строке которого 1, а в остальных - нули. ,
,
 ,
,
 , то для нахождения числа q получим характеристическое уравнение вида
, то для нахождения числа q получим характеристическое уравнение вида .
. . В случае жестких систем используются более узкие определения устойчивости.
. В случае жестких систем используются более узкие определения устойчивости.


