
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула (3.7) и есть итерационная формула метода Ньютона для приближенного решения системы нелинейных уравнений.Содержание книги
Поиск на нашем сайте
Замечание. В таком виде уравнение (3.7) используется редко в виду того, что на каждой итерации нужно находить обратную матрицу. Поэтому поступают следующим образом: вместо системы (3.6) решают систему линейных алгебраических уравнений вида
Это система линейных алгебраических уравнений относительно поправки Dx(n+1)= x(n+1)- x(n). Затем полагают
Сходимость метода
Теорема. Пусть в некоторой окрестности решения х системы (3.1) функции fi (при i=
где n - номер итерации. Метод Ньютона сходится с квадратичной скоростью. На практике используется следующий критерий остановки:
Решение проблемы собственных значений
Пусть дана квадратная матрица A размерностью (m*m) и существует такое число l, что выполняется равенство
тогда такое число l называется собственным значением матрицы А, а x – соответствующим ему собственным вектором. Перепишем это равенство в эквивалентной форме
Система (4.1) - однородная система линейных алгебраических уравнений. Для существования нетривиального решения системы (4.1) должно выполняться условие
Определитель в левой части уравнения является многочленом m-ой степени относительно l, его называют - характеристическим определителем (характеристическим многочленом). Следовательно, уравнение (4.2) имеет m корней или m собственных значений. Среди них могут быть как действительные, так и комплексные корни. Задача вычисления собственных значений сводится к нахождению корней характеристического многочлена (4.2). Корни могут быть найдены одним из итерационных методов (в частности методом Ньютона). Если найдено некоторое собственное значение матрицы A, то подставив это число в систему (4.1) и решив эту систему однородных уравнений, находим собственный вектор х, соответствующий данному собственному значению.
Собственные вектора будем при нахождении нормировать (вектор х умножаем на || х ||-1, и таким образом они будут иметь единичную длину), нахождение собственных значений матрицы A и соответствующих им собственных векторов и есть полное решение проблемы собственных значений. А нахождение отдельных собственных значений и соответствующих им векторов - называется решением частной проблемы собственных значений. Эта проблема имеет самостоятельное значение на практике. Например, в электрических и механических системах собственные значения отвечают собственным частотам колебаний, а собственные вектора характеризуют соответствующие формы колебаний. Эта задача легко решается для некоторых видов матриц - диагональных, треугольных и трехдиагональных матриц. К примеру определитель треугольной или диагональной матрицы равен произведению диагональных элементов, тогда и собственные числа равны диагональным элементам. Пример 1. Матрица А – диагональная det(А-lЕ)= Собственными векторами для матрицы А будут единичные векторы
Пример 2. Найдем собственные числа матрицы
Составим характеристический многочлен
Используя метод Ньютона, определим один из корней уравнения Р3(l)=0, а именно l1» -7.87279. Разделив многочлен Существуют прямые методы нахождения собственных значений и итерационные методы. Прямые методы неудобны для нахождения собственных значений для матриц высокого порядка. В таких случаях с учетом возможностей компьютера более удобны итерационные методы. Прямые методы 4.1.1 Метод Леверрье
Метод разделяется на две стадии: - раскрытие характеристического уравнения, - нахождение корней многочлена.
Пусть det(A-lE) - есть характеристический многочлен матрицы А ={aij} (i,j=1,2,…,m), т.е. Рассмотрим суммы вида
где В этом случае при k£m справедливы формулы Ньютона для всех (1£k£ m)
Откуда получаем
Следовательно, коэффициенты характеристического многочлена р i можно определить, если известны суммы S1,S2,...,Sm. Тогда схема алгоритма раскрытия характеристического определителя методом Леверрье будет следующей: 1) вычисляем степень матрицы: Ак=Ак-1*А для k=1,…,m; 2) определяют Sk - суммы элементов стоящих на главной диагонали матриц Ак; 3) по формулам (4.5) находят коэффициенты характеристического уравнения рi (i=1,2,…,m). 4.1.2 Усовершенствованный метод Фадеева
Алгоритм метода: 1) вычисляют элементы матриц A1,A2,..,Am:
(в конце подсчета Bm нулевая матрица для контроля);
2) определяют коэффициенты характеристического уравнения рi q1 = -р1, q2 = -р2,..., qm = -рm. Существуют и другие методы раскрытия характеристического определителя: метод Крылова, Данилевского и др.
4.1.3 Метод Данилевского Две матрицы A и B называются подобными, если одна получается из другой путем преобразования с помощью некоторой не вырожденной матрицы S:
B=S-1*AS,
если это равенство справедливо, то матрицы A и B подобны, а само преобразование называется преобразованием подобия (переход к новому базису в пространстве m - мерных векторов). Пусть y - результат применения матрицы A к вектору х
y =A* х.
Сделаем замену переменных:
x =S* x ', y =S* y'.
Тогда равенство y =A* х преобразуется к виду
y' =S-1*A*S* x'.
В этом случае матрица B и матрица A имеют одни и те же собственные числа. Это можно легко увидеть раскрыв определитель
Следовательно, матрицы A и B - подобные, имеют одни и те же собственные значения. Но собственные векторы х и х’ – не совпадают, они связаны между собой простым соотношением
х = S* х '.
Такую матрицу A с помощью преобразования подобия или же последовательности таких преобразований можно привести к матрице Фробениуса вида:
Детерминант матрицы F det (F) можно разложить по элементам первой строки:
Тогда коэффициенты характеристического многочлена матрицы А будут р1 = f11 , p2 = f12,…, pn = f1m.
Второй случай. Матрицу А преобразованием подобия можно привести к матрице В верхнего треугольного вида
Тогда собственными числами будут диагональные элементы матрицы B:
Третий случай. Матрицу A с помощью преобразования подобия можно привести к Жордановой форме
где li - собственные числа матрицы A; Si - константы (0 или 1); если Si=1, то li=li+1.
К четвёртому случаю относятся матрицы, которые с помощью преобразования подобия можно привести к диагональному виду (матрица простой структуры):
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.255.227 (0.01 с.) |

 ) дважды непрерывно дифференцируемы и матрица Якоби не вырождена. Тогда найдется такая малая d окрестность вокруг решения х, что при выборе начального приближения x 0 из этой окрестности итерационный метод (3.7) не выйдет за пределы этой окрестности решения и справедлива оценка вида
) дважды непрерывно дифференцируемы и матрица Якоби не вырождена. Тогда найдется такая малая d окрестность вокруг решения х, что при выборе начального приближения x 0 из этой окрестности итерационный метод (3.7) не выйдет за пределы этой окрестности решения и справедлива оценка вида ,
, .
. ,
, = 0.
= 0.
 . Тогда
. Тогда , а характеристическое уравнение
, а характеристическое уравнение  имеет трехкратный корень l=а.
имеет трехкратный корень l=а.
 .
.
 на (l-l1) получим многочлен второй степени:
на (l-l1) получим многочлен второй степени:  =l2 + 3.02711l + 2.66765. Решив квадратное уравнение, находим оставшиеся два корня:l2,3» -1.51356 ± 0.613841 * i (комплексное сопряженные корни).
=l2 + 3.02711l + 2.66765. Решив квадратное уравнение, находим оставшиеся два корня:l2,3» -1.51356 ± 0.613841 * i (комплексное сопряженные корни). , и l1,l2,…,lm - есть полная совокупность корней этого многочлена (полный спектр собственных значений).
, и l1,l2,…,lm - есть полная совокупность корней этого многочлена (полный спектр собственных значений).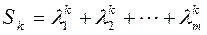 (k=1,2,…,m), т.е.
(k=1,2,…,m), т.е. ,
,
 - след матрицы.
- след матрицы. ,
,

 .
. .
. .
. .
. .
.
 ,
, ,
,


