
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
У которой, как известно, собственными числами являются диагональные элементы.Содержание книги
Поиск на нашем сайте
4.1.4 Метод итераций определения первого собственного числа матрицы.
Пусть дано характеристическое уравнение:
det(A -l* E) = 0,
где l1, l2,..., ln - собственные значения матрицы А. Предположим, что |l1|>|l2|³|l3|³…³|lm|, т.е. l1 – наибольшее по модулю собственное число. Тогда для нахождения приближенного значения λ1 используется следующая схема: 1) выбирают произвольно начальный вектор у(0); 2) строят последовательность итераций вида:
3) выбирают
где yi – соответствующие координаты векторов y(m+1) и y(m). Возникает вопрос выбора начального вектора у(0). При неудачном выборе можем не получить значения нужного корня, или же предела может не существовать. Этот факт при вычислении можно заметить по прыгающим значениям этого отношения, следовательно, нужно изменить у(0). В качестве первого собственного вектора можно взять вектор у(n+1) и пронормировать его. Пример. Найти наибольшее по модулю собственное значение и соответствующий ему собственный вектор матрицы А
1) Выбираем начальный вектор
2) Вычисляем последовательно векторы y(1), y(2), …, y(10). Вычисления помещаем в таблицу 2.
Таблица 2 – Вычисление векторов y(n+1)
3) Вычисляем отношения координат векторов
4) Вычисляем λ1 как среднее арифметическое
5) Определим соответствующий числу λ1 собственный вектор:
Нормируем y(10), разделив на длину вектора
получим вектор Далее можем определить второе собственное число
где i=1,2,…,n. При вычислении собственных чисел подобным образом, будет накапливается ошибка. Данная методика позволяет приближенно оценить собственные значения матрицы.
Задача приближения функции
Постановка задачи. Пусть на отрезке [a,b] задана функция у= f(x) своими n+1 значениями Допустим, что вид функции f(x) неизвестен. На практике часто встречается задача вычисления значений функции у= f(x) в точках х, отличных от Определение. Точки Требуется найти аналитическое выражение функции F(x), совпадающей в узлах интерполяции со значениями данной функции, т.е.
Определение. Процесс вычисления значений функции F(x) в точках отличных от узлов интерполирования называется интерполированием функции f(x). Если Геометрически задача интерполирования функции одной переменной означает построение кривой, проходящей через заданные точки
x
Рисунок 5 - Геометрическая иллюстрация задачи интерполирования функции
Задача становится однозначной, если в качестве F(x) выбрать многочлен степени не выше n, такой что:
F
Определение. Многочлен F Определение. Когда многочлен F(x) выбирается в классе степенных функций, то интерполяция называется параболической. Знание свойств функции f позволяет осознанно выбирать класс G аппроксимирующих функций. Широко используется класс функций вида
являющихся линейными комбинациями некоторых базисных функций
Фm(хi)=yi, (i=0,1,…,n). (5.2)
Покажем, что условие (5.2) позволяет найти приближающую функцию единственным образом
Система (5.3) есть система линейных алгебраических уравнений относительно коэффициентов с0,с1,…,сm. Эта система n линейных уравнений имеет единственное решение, если выполняется условие m=n и определитель квадратной матрицы Р
Определение. Система функций Пример. При m£n система функций 1 ,х,х2,…,хm линейно независима в точках х0,х1,…,хn, если они попарно различны.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.74.192 (0.007 с.) |

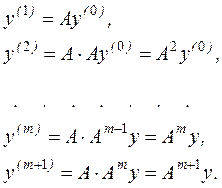
 , тогда
, тогда или
или  ,
,
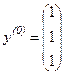 .
.


 .
.


 ,
,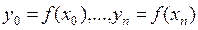 , в точках
, в точках 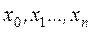 .
. . Кроме того, в некоторых случаях, не смотря на то, что аналитическое выражение у=f(x) известно, оно может быть слишком громоздким и неудобным для математических преобразований (например, специальные функции). Кроме этого значения yi могут содержать ошибки эксперимента.
. Кроме того, в некоторых случаях, не смотря на то, что аналитическое выражение у=f(x) известно, оно может быть слишком громоздким и неудобным для математических преобразований (например, специальные функции). Кроме этого значения yi могут содержать ошибки эксперимента.
 , то задача вычисления приближенного значения функции в т. х называется интерполированием, иначе - экстраполированием.
, то задача вычисления приближенного значения функции в т. х называется интерполированием, иначе - экстраполированием. (рисунок 5). То есть задача в такой постановке может иметь бесконечное число решений.
(рисунок 5). То есть задача в такой постановке может иметь бесконечное число решений. у
у


 x
x  x
x  x
x  х
х (x
(x  (5.1)
(5.1)
 ,...,с
,...,с  , которые находятся в зависимости от вида приближения. Функцию Фm(х) называют обобщенным многочленом по системе функций j0(х),j1(х),…,jm(х), а число m – его степенью. Назовем обобщенный многочлен Фm(х) интерполяционным, если он удовлетворяет условию
, которые находятся в зависимости от вида приближения. Функцию Фm(х) называют обобщенным многочленом по системе функций j0(х),j1(х),…,jm(х), а число m – его степенью. Назовем обобщенный многочлен Фm(х) интерполяционным, если он удовлетворяет условию
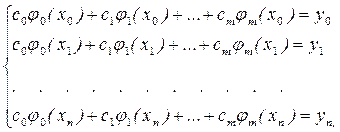 (5.3)
(5.3)



