
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение нелинейных уравнений и систем нелинейных уравненийСодержание книги
Поиск на нашем сайте
Метод простых итераций
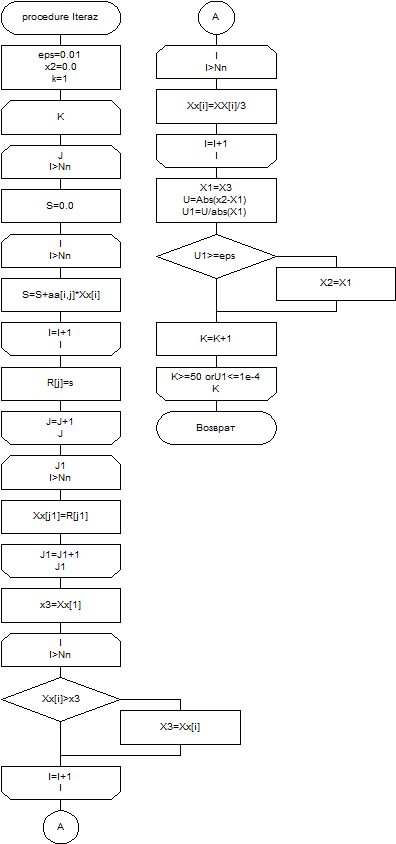
Порядок выполнения лабораторной работы: 1. Найти нулевое приближение решения; 2. Преобразовать систему f(x) = 0 к виду х = Ф(х); 3. Проверить условие сходимости метода. Схема алгоритма приведена на рисунке 20. Пример. Решить методом простых итераций систему
В качестве нулевого приближения выберем точку х=1, у = 2.2, z = 2. Преобразуем систему к виду
Текст программы:
PROCEDURE Iteraz; Var I,J,K,J1: Integer; S,U,U1: Real; X2,X3,Eps: Real; R: tvector; Begin Eps:=0.01; X2:=0.0; K:=1; Repeat For J:=1 To Nn Do Begin S:=0.0; For I:=1 To Nn Do Begin S:=S+Aa[i,j]*Xx[i]; End; R[j]:=S; End; For J1:=1 To Nn Do Begin Xx[j1]:=R[j1]; End; X3:=Xx[1]; For I:=1 To Nn Do Begin If (Xx[i]>=X3) Then X3:=Xx[i]; Еnd; For I:=1 To Nn Do Begin Xx[i]:=Xx[i]/X3; End; X1:=X3; U:=Abs(X2-X1); U1:=U/Abs(X1); If (U1>=Eps) Then X2:=X1; K:=K+1; Until ((K>=50)or(U1<=1e-4)) End;
Вычисления по программе привели к следующим результатам: X(1)= 1.1132 Х(2)= 2.3718 Х(3)= 2.1365 Количество итераций:5
Рисунок 20 - Схема алгоритма метода простых итераций Метод Ньютона
Программу можно использовать для решения систем не выше десятого порядка. Входные параметры: n — число уравнений системы (совпадает с числом неизвестных), n£10; х—массив из n действительных чисел, содержащий начальное приближение решения; f— имя внешней процедуры f(n, х, у), вычисляющей по заданным значениям х, расположенным в элементах массива х, текущие значения функции f и размещающей их в элементах массива у; g — имя внешней процедуры g(n, x, d), вычисляющей по заданным значениям х из массива х элементы матрицы Выходные параметры: х — массив из n действительных чисел (он же входной) содержит при выходе из подпрограммы приближенное значение решения; k—количество итераций. Порядок выполнения лабораторной работы: 1. Определить из геометрических соображений начальное приближение решения. 2. Составить подпрограммы f и g для вычисления значений f и 3. Составить головную программу, содержащую описание массива х, имен f и g, присвоение фактических значений параметрам n, х, eps, обращение к ТNUTON и печать результатов. 4. Провести вычисления на ЭВМ. Схема алгоритма приведена на рисунке 21. Пример.Решить систему уравнений
Текст программы:
procedure TNuton;
var a: T2DArray; i, j: byte; finish: boolean; begin IterCount:= 0; SetLength(a, UrCount); for i:= 0 to High(a) do SetLength(a[i], UrCount + 1); repeat { Заполнение матрицы частных производных } for i:= 0 to High(a) do begin for j:= 0 to High(a[i])-1 do a[i, j]:= DerivativeFn(i, j, Results); a[i, High(a[i])]:= -Poliz.ExternFn(i, Results); end; { Решение полученной СЛАУ методом Гаусса } SetLength(Gauss.Base, Length(a)); for i:= 0 to High(a) do begin SetLength(Gauss.Base[i], Length(a[i])); for j:= 0 to High(a[i]) do Gauss.Base[i, j]:= a[i, j]; end; try Gauss.Solve; except raise Exception.Create('Данную систему этим методом решить невозможно!'); end; { Получение очередного приближения решения СНАУ } finish:= false; for i:= 0 to High(Results) do begin Results[i]:= Results[i] + Gauss.Results[i]; if not finish then finish:= (Abs(Gauss.Results[i]/Results[i]) > Eps); end; inc(IterCount); until not finish; end;
В результате вычисления по программе получены следующие результаты: X(1)= 1.1132 Х(2)= 2.3718 Х(3)= 2.1365 Количество итераций:4
Рисунок 21 - Схема алгоритма метода Ньютона
Варианты заданий
Таблица 4
Тема лабораторной работы №4 для контроля знаний проиллюстрирована контрольно – обучающей программой. Лабораторная работа № 5 Решение проблемы собственных значений и собственных векторов Точные методы Метод Леверрье
Входные параметры: n—целое положительное число, равное порядку n системы; Выходные параметры: b—массив из n действительных чисел, при выходе из программы содержит решение системы. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE Liver (Var VeS:Tvector;Nn:Integer);; Label 35,270,220,100,80,190,500,250,350,120,10; Var I,J,K,T:Integer; Y,Yy:tvector; {A,Aa:Mas;} S,C,Q,P,H,D,U,M,V,F,W,Yyy,Z,L,R,X,Aaa,B:Real; Sq,Sq1: Real; F1: TEXT; Begin Assign(F1,'last.out'); Rewrite(F1); For I:=Nn Downto 1 Do Y[i+1]:=VeS[i];
Y[1]:=1; K:=1; 35: T:=1; C:=Y[2]/Y[1]; If (Nn=1) Then Begin P:=-C; Q:=0; Goto 270; End; If (Nn=2) Then Begin H:=C*C/4-Y[3]/Y[1]; Goto 220; End; M:=10;C:=4;D:=8;U:=4; V:=8;F:=1;W:=2;T:=0; 80: If(M<>10) Then Goto 100; P:=C;M:=0;Q:=D;C:=U;D:=V; U:=P;V:=Q;Yyy:=C;Z:=D;F:=-F; 100:M:=M+1;H:=0;Q:=Y[1];P:=Y[2]-C*Q;L:=Q; 120:For J:=3 To Nn Do Begin R:=P;P:=Y[j]-C*R-D*Q;Q:=R; R:=L;L:=Q-C*R-H*D;H:=R; End; Q:=Y[Nn+1]-D*Q; S:=L+C*R; If (T=0) Then Begin X:=D*R;H:=R*X+S*L; If H=0 Then Goto 80; End; C:=C+(P*S-Q*R)/H; D:=D+(P*X+Q*L)/H; If ((C-Yyy+D-Z)<>0) Then Goto 190; If (F=-W) Then Begin writeln('Љ®аҐм Ґ ©¤Ґ'); Goto 500; End; W:=-F; 190:H:=C*C/4-D; Sq:=Sqrt((Q-P*C/2)*(Q-P*C/2)+P*P*Abs(H)); If (Sq>0.0000001) Then Goto 80; T:=0; Y[2]:=Y[2]-C*Y[1]; For J:=3 To Nn-1 Do Begin Y[j]:=Y[j]-C*Y[j-1]-D*Y[j-2];End; 220:P:=-C/2; Q:=Sqrt(Abs(H)); If(h>=0) Then Begin M:=P+Q;P:=P-Q;Q:=0; Goto 250; End; M:=P; 250:write(F1,'p',k,'=',m:9:4,' + i',q:7:4);K:=K+1;{Ves[k-1]:=M;}WriteLn(F1,''); 270:write(F1,'p',k,'=',p:9:4,' + i',-q:7:4);K:=K+1;{Ves[k-1]:=P;}WriteLn(F1,''); If(t<>0) Then Goto 350; Nn:=Nn-2; Aaa:=0; Sq1:=Sqrt((S-R*C/2)*(S-R*C/2)+R*R*Abs(H)); If (Sq1<=0.0000001) Then Aaa:=1; B:=0; If (Nn>=2) Then B:=1; If((Aaa+B)=2) Then Begin T:=1; Goto 120; End; Goto 35;350:500: Close(F1); End;
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Варианты заданий для нахождения собственных значений и собственных векторов матрицы приведены в таблице 5. Метод Фадеева
Входные параметры: n—целое положительное число, равное порядку n системы; а — массив из n х n действительных чисел, содержащий входную матрицу. Выходные параметры: q—массив из n действительных чисел при выходе из программы содержит решение системы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.218.25 (0.009 с.) |

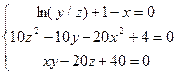

 ,которая размещается в массиве d размерности n x n; eps — значение условия окончания итерационного процесса.
,которая размещается в массиве d размерности n x n; eps — значение условия окончания итерационного процесса.









