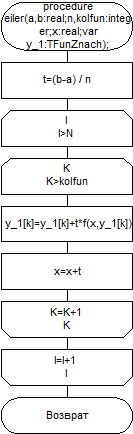Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема алгоритма приведена на рисунке 23.Содержание книги
Поиск на нашем сайте
Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5| Текст программы:
procedure Fadeev(n:integer;a:tmatr;var q:tvector); var Aa,E,B:tmatr; i,j:integer; begin for i:=1 to n do for j:=1 to n do if i<>j then e[i,j]:=0 else e[i,j]:=1; Aa:=a; q[1]:=spA(n,Aa); MulChislo(n,q[1],e,b); MatrVich(n,Aa,b,b); for i:=2 to n do begin MulMatr(n,a,b,Aa); q[i]:=-spA(n,Aa)/i; MulChislo(n,q[i],e,b); MatrVich(n,Aa,b,b); end; end;
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Рисунок 23 - Схема алгоритма метода Фадеева
Варианты заданий для нахождения собственных значений и собственных векторов матрицы приведены в таблице 5.
Метод Крылова
Входные параметры: n—целое положительное число, равное порядку n системы; а — массив из n х n действительных чисел, содержащий входную матрицу. Выходные параметры: q—массив из n действительных чисел при выходе из программы содержит решение системы. Схема алгоритма приведена на рисунке 24. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE Krylov(Nn:integer; A: TMatr;Var Y:TVector); Label 2; Var I,J,K,T,Nn1:Integer; yy:TVector; aa:TMatr; s,c,q,p,h,d,u, m,v,f,w,yyy,z, l,r,x,aaa,b: Real; Begin form3.Caption:='Крылов'; Nn1:=Nn; For I:=1 To Nn Do Yy[i]:=I*Trunc(10*ranDom); 2:For I:=Nn Downto 1 Do Begin Y:=Yy; For J:=1 To Nn Do Aa[j,i]:=Yy[j]; For J:=1 To Nn Do Begin S:=0; For K:=1 To Nn Do S:=S+A[j,k]*Y[k]; Yy[j]:=S; End; End; For I:=1 To Nn Do Y[i]:=-Yy[i]; Simq(Nn1,Aa,Y,K); If(K=1) Then Begin For I:=1 To Nn Do Yy[i]:=I*I*trunc(7*ranDom); Goto 2; End; End;
Рисунок 24 - Схема алгоритма метода Крылова
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Варианты заданий для нахождения собственных значений и собственных векторов матрицы приведены в таблице 5. Тема лабораторной работы №5 для контроля знаний проиллюстрирована контрольно – обучающей программой. Лабораторная работа № 6 Решение проблемы собственных значений и собственных векторов Итерационные методы Метод QR-разложения
Входные параметры: nn—целое положительное число, равное порядку n системы; а — массив из n х n действительных чисел, содержащий входную матрицу.
Выходные параметры: R_1, R_2—массив из n действительных чисел при выходе из программы содержит решение системы. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE Qr (Var Nn:Integer;Var A:Tmatr;Var R_1:Tvector;Var R_2:Tvector);; Var I,J,K,L,M,Na,Its: Integer; I1,M1,N1,L1,N: Integer; M3,U1,U11,U2: Real; Q,P,R,S,T,U,X,Y,Z,W: Real; Aa: tMatr; r1,r2:tvector; Label NexTw,NexTit,Cont_1,Cont_2,Cont_3; Label Onew,TwOw,Fin; Begin Aa:=A; N:=Nn; for i:=0 to Nn do begin r1[i]:=0; r2[i]:=0; end; T:=0.0; NexTw: If (N=0) Then Goto Fin; Its:=0; Na:=N-1; M3:=1.0e-11; NexTit: For L:=N DownTo 2 Do Begin U:=Abs(Aa[l,l-1]); U1:=M3*(Abs(Aa[l-1,l-1])+Abs(Aa[l,l])); If (U<=U1) Then Goto Cont_1; End; L:=1; Cont_1: X:=Aa[n,n]; If(L=N) Then Goto Onew; Y:=Aa[na,na]; W:=Aa[n,na]*Aa[na,n]; If(L=Na) Then Goto Twow; If(Its=30) Then Goto Fin; If((Its=10)And(Its=20)) Then Begin T:=T+X; For I:=1 To N Do Begin Aa[i,i]:=Aa[i,i]-X; End;{} S:=Abs(Aa[n,na])+Abs(Aa[na,n-2]); X:=0.75*S; Y:=0.75*S; W:=-0.4375*S*S; End; Its:=Its+1; For M:=N-2 Downto L Do Begin Z:=Aa[m,m]; R:=X-Z; S:=Y-Z; P:=(R*S-W)/Aa[m+1,m]+Aa[m,m+1]; Q:=Aa[m+1,m+1]-Z-R-S; R:=Aa[m+2,m+1]; S:=Abs(P)+Abs(Q)+Abs(R); P:=P/S; Q:=Q/S; R:=R/S; If(M=L) Then Goto Cont_2; U11:=Abs(Aa[m,m-1])*(Abs(Q)+Abs(R)); U2:=M3*Abs(P)*(Abs(Aa[m-1,m-1])+Abs(Z)+Abs(Aa[m+1,m+1])); If(U11<=U2) Then Goto Cont_2; End; Cont_2: For I:=M+2 To N Do Begin Aa[i,i-2]:=0.0; End; For I:=M+3 To N Do Begin Aa[i,i-3]:=0.0; End; For K:=M To Na Do Begin If (K<>M) Then Begin; P:=Aa[k,k-1]; Q:=Aa[k+1,k-1]; If(K<>Na) Then R:=Aa[k+2,k-1] Else R:=0.0; X:=Abs(P)+Abs(Q)+Abs(R); If(X=0.0) Then Goto Cont_3; P:=P/X; Q:=Q/X; R:=R/X; End; S:=Sqrt(P*P+Q*Q+R*R); If(P<0.0) Then S:=-S; If(K<>M) Then Aa[k,k-1]:=-S*X Else If(L<>M) Then Aa[k,k-1]:=-Aa[k,k-1]; P:=P+S; X:=P/S; Y:=Q/S; Z:=R/S;Q:=Q/P; R:=R/P; For J:=K To N Do Begin P:=Aa[k,j]+Q*Aa[k+1,j]; If (K<>Na) Then Begin P:=P+R*Aa[k+2,j]; Aa[k+2,j]:=Aa[k+2,j]-P*Z; End; Aa[k+1,j]:=Aa[k+1,j]-P*Y; Aa[k,j]:=Aa[k,j]-P*X; End; If((K+3)<N) Then J:=K+3 Else J:=N; For I:=L To J Do Begin P:=X*Aa[i,k]+Y*Aa[i,k+1]; If(K<>Na) Then Begin; P:=P+Z*Aa[i,k+2]; Aa[i,k+2]:=Aa[i,k+2]-P*R; End; Aa[i,k+1]:=Aa[i,k+1]-P*Q; Aa[i,k]:=Aa[i,k]-P; End; Cont_3: End; Goto NexTit; Onew: R1[n]:=X+T; {R1-ўҐй} R2[n]:=0.0; {Cnt[n]:=its;} N:=Na; Goto Nextw; Twow: P:=(Y-X)/2.0; Q:=P*P+W; Y:=Sqrt(Abs(Q)); {Cnt[n]:=-its; Cnt[na]:=its;} X:=X+T; If(Q>0.0) Then Begin If(P<0.0) Then Y:=-1.0*Y; Y:=P+Y; R1[na]:=X+Y; R1[n]:=X-W/Y; R2[na]:=0.0; R2[n]:=0.0; End Else Begin R1[na]:=X+P; R1[n]:=X+P; R2[na]:=Y; R2[n]:=-1.0*Y;End; N:=N-2; Goto Nextw; Fin: r_1:=r1; r_2:=r2; End;
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Варианты заданий для нахождения собственных значений и собственных векторов матрицы приведены в таблице 5.
Метод обратных итераций
Входные параметры: nn—целое положительное число, равное порядку n системы; Aа — массив из n х n действительных чисел, содержащий входную матрицу, eps – малое число для условия окончания итерационного процесса.
Выходные параметры: V0,V1—массив из n действительных чисел при выходе из программы содержит решение системы, it – количество итераций. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE IObrIter(Nn:integer;Aa:tmatr;lam,lam1,eps:real;var V0,V1:tvector;var it:byte); var x,x1:tvector; c,c1:extended; nev:real; i,j,k,p:integer; i1:byte; aa1:tmatr; rv,rv1:tvector; begin it:=1; for i:=1 to 2*nn do for j:=1 to 2*nn do begin if (i<=Nn)and(j<=Nn)then if i=j then aa1[i,i]:=aa[i,i]-lam else aa1[i,j]:=aa[i,j]; if (i<=Nn)and(j>Nn) then if j=Nn+i then aa1[i,j]:=-lam1 else aa1[i,j]:=0; if (i>Nn)and(j<=Nn)then if i=j+Nn then aa1[i,j]:=-lam1 else aa1[i,j]:=0; if (i>Nn)and(j>Nn)then if i=j then aa1[i,j]:=aa[i-nn,j-nn]-lam else aa1[i,j]:=aa[i-nn,j-nn]; end; for i:=1 to Nn do rv1[i]:=1; for i:=Nn+1 to 2*nn do rv1[i]:=0; repeat rv:=rv1; rv1:=rv; simq(2*Nn,AA1,rv1,p);{ c:=rv1[1]; c1:=rv1[nn+1]; for i1:=1 to Nn do begin if rv1[i1]<c then c:=rv1[i1]; if rv1[i1+nn]<c1 then c1:=rv1[i1+nn]; end;} for i1:=1 to Nn do begin rv1[i1,1]:=rv1[i1,1]/c; rv1[i1,2]:=rv1[i1,2]/c1; end;} c:=0; c1:=0; for i:=1 to Nn do begin c:=c+sqr(rv1[i]); c1:=c1+sqr(rv1[i+nn]); end; c:=sqrt(c); c1:=sqrt(c1); nev:=0; for i:=1 to Nn do begin rv1[i]:=rv1[i]/c; rv1[i+nn]:=rv1[i+nn]/c1; nev:=nev+(sqr(rv[i])+sqr(rv[i+nn])-sqr(rv1[i])-sqr(rv1[i+nn])); end; nev:=sqrt(nev); inc(it); until (nev<eps)or (it>15); for i:=1 to Nn do begin v0[i]:=rv1[i]; v1[i]:=rv1[i+nn]; end; end;
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Варианты заданий
Таблица 5
Тема лабораторной работы №6 для контроля знаний проиллюстрирована контрольно – обучающей программой.
Лабораторная работа № 7 Приближение функций
Интерполяционный полином Лагранжа
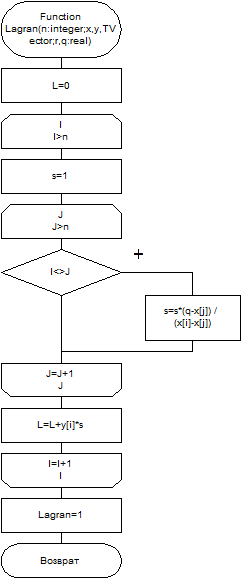
Входные параметры: N - число узлов интерполяции; y - массив размерности n, содержащий значения функции в узлах интерполяции; x-массив размерности n, содержащий значения узлов интерполяции; q-точка в которой вычисляем значения функции интерполяции. Выходные параметры: приближенное значение функции в точке q; графическая интерпретация результата. Схема алгоритма приведена на рисунке 25. Задание. Аппроксимировать табличную функцию с помощью интерполяционного полинома Лагранжа.
Текст программы:
function Lagran(n:integer;x,y:TVector;q:real):real; var i,j:integer; l,s:real; begin L:=0; for i:=1 to n do begin s:=1; for j:=1 to N do if j<>i then s:=s*(q-x[j])/(x[i]-x[j]); L:=L+y[i]*s; end; Lagran:=l end
Вычисления по программе привели к следующим результатам:
X=1 Y=2,05 X=1,5 Y=2,38 X=2 Y=1,94 X=2,5 Y=1,83 X=3 Y=1,92 X=3,5 Y=1,94 X=4 Y=1,87 X=4,5 Y=1,78 X=5 Y=1,77 X=5,5 Y=1,83 X=6 Y=1,88 X=6,5 Y=1,83 X=7 Y=1,71 X=7,5 Y=1,59 X=8 Y=1,6 X=8,5 Y=1,67 X=9 Y=1,56 X=9,5 Y=1,09 X=10 Y=1,4
Рисунок 25 - Схема алгоритма приближения функций формулой Лагранжа
Варианты заданий для решения задачи приближения функций приведены в таблице 6.
Аппроксимация функций с помощью кубического сплайна
Входные параметры: N - число узлов интерполяции; y - массив размерности n, содержащий значения функции в узлах интерполяции; x-массив размерности n, содержащий значения узлов интерполяции; q-точка в которой вычисляем значения функции интерполяции. Выходные параметры: приближенное значение функции в точке q; графическая интерпретация результата. Схема алгоритма приведена на рисунке 26. Задание. Аппроксимировать табличную функцию с помощью кубического сплайна.
Текст программы:
Procedure Spline3(N:integer;X,Y:mas;S0,SN:real;Var A,B,C,D:mas); Var F: Mas; H2,H3,p: real; i,j: integer; Begin H2:=X[2]-X[1]; H3:=X[3]-X[2]; A[1]:=(2*(H2+H3))/H3; f[1]:=(6/h3)*(((y[3]-y[2])/h3)-((y[2]-y[1])/h2))-(h2*s0)/h3; For i:=4 to n-1 do begin h2:=x[i-1]-x[i-2]; h3:=x[i]-x[i-1]; a[i-2]:=(2/h3)*(h2+h3); b[i-2]:=h2/h3; f[i-2]:=(6/h3)*(((y[i]-y[i-1])/h3-((y[i-1]-y[i-2])/h2))); end; h2:=x[n-1]-x[n-2]; h3:=x[n]-x[n-1]; p:=2*(h2+h3); b[1]:=h2/p; f[n-2]:=(6/p)*(((y[n]-y[n-1])/h3)-((y[n-1]-y[n-2])/h2))-(h3*sn)/p; d[1]:=1/a[1]; c[1]:=f[1]; For i:=2 to n-3 do begin d[i]:=1/(a[i]-b[i]*d[i-1]); c[i]:=f[i]-b[i]*d[i-1]*c[i-1]; end; d[n-2]:=(f[n-2]-b[1]*d[n-3]*c[n-3])/(1-b[1]*d[n-3]); For i:=n-3 downto 1 do d[i]:=d[i]*(c[i]-d[i+1]); c[1]:=s0; c[n]:=sn; For i:=2 to n-1 do c[i]:=d[i-1]; For i:=1 to n do begin a[i]:=0; b[i]:=0; d[i]:=0; end; For i:=2 to n do begin h2:=x[i]-x[i-1]; d[i]:=(c[i]-c[i-1])/h2; b[i]:=h2*c[i]/2-(Sqr(h2))*d[i]/6+(y[i]-y[i-1])/h2; a[i]:=y[i]; end; end; Вычисления по программе привели к следующим результатам:
X=1 Y=2,21 X=1,5 Y=2,06 X=2 Y=1,94 X=2,5 Y=2,00 X=3 Y=1,92 X=3,5 Y=1,99 X=4 Y=1,87 X=4,5 Y=1,88 X=5 Y=1,77 X=5,5 Y=1,91 X=6 Y=1,88 X=6,5 Y=1,90 X=7 Y=1,71 X=7,5 Y=1,71 X=8 Y=1,6 X=8,5 Y=1,66 X=9 Y=1,56 X=9,5 Y=1,57 X=10 Y=1,4
Рисунок 26 - Схема алгоритма приближения функций с помощью сплайнов Варианты заданий для решения задачи приближения функций приведены в таблице 6.
Приближение формулами Ньютона
Входные параметры: N - число узлов интерполяции; y - массив размерности n, содержащий значения функции в узлах интерполяции; x-массив размерности n, содержащий значения узлов интерполяции; q-точка в которой вычисляем значения функции интерполяции.
Выходные параметры: приближенное значение функции в точке q; графическая интерпретация результата. Схема алгоритма приведена на рисунке 27. Задание. Аппроксимировать табличную функцию с помощью формул Ньютона.
Текст программы:
function PribNew(n:integer;a,b:TVector;x:Real):real; function GetRazdRazn(k,l:integer;m:TMatr):real; begin GetRazdRazn:=m[k,l-k+1]; end; var i,j:integer; s,p:real; M:tmatr; begin TabRazdRazn(n,a,b,M); S:=b[1]; for i:=1 to N-1 do begin P:=1; for j:=1 to i do P:=P*(x-a[j]); s:=s+P*GetRazdRazn(1,i+1,m); end; PribNew:=s; end;
Вычисления по программе привели к следующим результатам:
X=1 Y=2,05 X=1,5 Y=2,38 X=2 Y=1,94 X=2,5 Y=1,83 X=3 Y=1,92 X=3,5 Y=1,94 X=4 Y=1,87 X=4,5 Y=1,78 X=5 Y=1,77 X=5,5 Y=1,83 X=6 Y=1,88 X=6,5 Y=1,83 X=7 Y=1,71 X=7,5 Y=1,59 X=8 Y=1,6 X=8,5 Y=1,67 X=9 Y=1,56 X=9,5 Y=1,09 X=10 Y=1,4
Рисунок 27 - Схема алгоритма приближения функций формулами Ньютона
Варианты заданий для решения задачи приближения функций приведены в таблице 6.
Аппроксимация функций методом наименьших квадратов.
Входные параметры: N - число узлов интерполяции; y - массив размерности n, содержащий значения функции в узлах интерполяции; x-массив размерности n, содержащий значения узлов интерполяции; q-точка в которой вычисляем значения функции интерполяции. Выходные параметры: приближенное значение функции в точке q; графическая интерпретация результата.
Схема алгоритма приведена на рисунке 28. Задание. Аппроксимировать табличную функцию многочленом второй степени методом наименьших квадратов.
Текст программы:
function Apr_Kv(n:integer;x,y:TVector;q:real):real; var i,j:integer; a:TMatr; b,c:TVector; s:real; begin a[1,1]:=N; s:=0; for i:=1 to N do s:=s+x[i]; a[1,2]:=s; a[2,1]:=s; s:=0; for i:=1 to N do s:=s+x[i]*x[i]; a[1,3]:=s; a[2,2]:=s; a[3,1]:=s; s:=0; for i:=1 to N do s:=s+x[i]*x[i]*x[i]; a[2,3]:=s; a[3,2]:=s; s:=0; for i:=1 to N do s:=s+x[i]*x[i]*x[i]*X[i]; a[3,3]:=s; s:=0; for i:=1to N do s:=s+y[i]; b[1]:=s; s:=0; for i:=1 to N do s:=s+y[i]*x[i]; b[2]:=s; s:=0; for i:=1 to N do s:=s+y[i]*x[i]*x[i]; b[3]:=s; j:=N; N:=3; LinSys(n,a,b,c); Apr_kv:=c[1]+c[2]*q+c[3]*q*q; N:=j; for i:=0 to N-1 do begin a:=apr_kv(x,y,i/10); end;
Вычисления по программе привели к следующим результатам:
A=-0,004 B=-0,0132 C=2,0147 X=1 Y=2,00 X=1,5 Y=1,99 X=2 Y=1,97 X=2,5 Y=1,95 X=3 Y=1,93 X=3,5 Y=1,91 X=4 Y=1,89 X=4,5 Y=1,86 X=5 Y=1,83 X=5,5 Y=1,80 X=6 Y=1,77 X=6,5 Y=1,73 X=7 Y=1,70 X=7,5 Y=1,66 X=8 Y=1,62 X=8,5 Y=1,57 X=9 Y=1,53 X=9,5 Y=1,48 X=10 Y=1,43
Рисунок 28 - Схема алгоритма аппроксимации функций методом наименьших квадратов Варианты заданий. Значения xi=i´0,1; i=1,2…20 одинаковые для всех вариантов
Таблица 6
Тема лабораторной работы №7 для контроля знаний проиллюстрирована контрольно – обучающей программой. Лабораторная работа №8 Решение задачи Коши Одношаговые методы
Метод Эйлера
Входные параметры: a,b – интервал приближения; n – количество точек приближения; Kolfun – порядок системы; x – начальное значение Выходные параметры: y_1 – массив из kolfun чисел, содержащий приближенное решение системы. Схема алгоритма показана на рисунке 29. Пример. Решить на отрезке [0,3] с шагом 0,1 задачу Коши
Текст программы:
procedure eiler (a,b:real;n,kolfun:integer;x:real;var y_1:TFunZnach);; var t:real; begin t:=(b-a)/n; for i:=1 to n do begin for k:=1 to kolfun do y_1[k]:=y_1[k]+t*f(x,y_1[k]);{F(y1,y2,x)} x:=x+t; end; end;
Вычисления по программе привели к следующим результатам:
x=0 y1=0 y2=0 x=0,1 y1=0 y2=0,1 x=0,2 y1=0,01 y2=0,19 x=0,3 y1=0,02 y2=0,29 x=0,4 y1=0,05 y2=0,38 x=0,5 y1=0,09 y2=0,47 x=0,6 y1=0,14 y2=0,55 x=0,7 y1=0,20 y2=0,62 x=0,8 y1=0,26 y2=0,68 x=0,9 y1=0,33 y2=0,74 x=1 y1=0,40 y2=0,79 x=1,1 y1=0,48 y2=0,84 x=1,2 y1=0,56 y2=0,88 x=1,3 y1=0,65 y2=0,91 x=1,4 y1=0,74 y2=0,94 x=1,5 y1=0,84 y2=0,97 x=1,6 y1=0,94 y2=0,99 x=1,7 y1=1,04 y2=1,01 x=1,8 y1=1,14 y2=1,03 x=1,9 y1=1,24 y2=1,04 x=2 y1=1,35 y2=1,06 x=2,1 y1=1,45 y2=1,07 x=2,2 y1=1,56 y2=1,08 x=2,3 y1=1,67 y2=1,09 x=2,4 y1=1,78 y2=1,10 x=2,5 y1=1,89 y2=1,11 x=2,6 y1=2,00 y2=1,11 x=2,7 y1=2,11 y2=1,12 x=2,8 y1=2,22 y2=1,12 x=2,9 y1=2,34 y2=1,13
Рисунок 29 - Схема алгоритма метода Эйлера
Варианты заданий для решения задачи Коши методом Эйлера приведены в таблице 7.
Метод прогноза и коррекции
Входные параметры: a,b – интервал приближения; n – количество точек приближения; Kolfun – порядок системы; x – начальное значение Выходные параметры: y_1 – массив из kolfun чисел, содержащий приближенное решение системы. Схема алгоритма показана на рисунке 30. Пример. Решить задачу Коши на отрезке [0,3] с шагом 0,1
Текст программы:
procedure prognoz(a,b:real;n,kolfun:integer;x:real;y_0:TFunZnach;var y_1:TFunZnach); var h:real; begin h:=(b-a)/n; for i:=1 to n do begin for k:=1 to kolfun do y_0[k]:=y_0[k]+h*f(x+0.5*h,y_0[k]+0.5*h*f(y_0[k],x)); x:=x+h; end; y_1:=y_0; end;
Вычисления по программе привели к следующим результатам:
x=0 y1=0 y2=0 x=0,1 y1=0,01 y2=0,1 x=0,2 y1=0,02 y2=0,19 x=0,3 y1=0,05 y2=0,29 x=0,4 y1=0,09 y2=0,38 x=0,5 y1=0,14 y2=0,46 x=0,6 y1=0,20 y2=0,53 x=0,7 y1=0,26 y2=0,60 x=0,8 y1=0,33 y2=0,67 x=0,9 y1=0,40 y2=0,72 x=1 y1=0,48 y2=0,77 x=1,1 y1=0,57 y2=0,81 x=1,2 y1=0,66 y2=0,85 x=1,3 y1=0,75 y2=0,88 x=1,4 y1=0,84 y2=0,91 x=1,5 y1=0,94 y2=0,94 x=1,6 y1=1,04 y2=0,96 x=1,7 y1=1,14 y2=0,98 x=1,8 y1=1,25 y2=1,00 x=1,9 y1=1,35 y2=1,01 x=2 y1=1,46 y2=1,02 x=2,1 y1=1,57 y2=1,03 x=2,2 y1=1,68 y2=1,04 x=2,3 y1=1,79 y2=1,05 x=2,4 y1=1,90 y2=1,06 x=2,5 y1=2,01 y2=1,07 x=2,6 y1=2,13 y2=1,07 x=2,7 y1=2,24 y2=1,08 x=2,8 y1=2,35 y2=1,08 x=2,9 y1=2,47 y2=1,09
Рисунок 30 - Схема алгоритма метода прогноза и коррекции
Варианты заданий для решения задачи Коши методом прогноза и коррекции приведены в таблице 7.
Метод Рунге-Кутта 4-го порядка
Входные параметры: a,b – интервал приближения; n – количество точек приближения; Kolfun – порядок системы; x – начальное значение Выходные параметры: y_1 – массив из kolfun чисел, содержащий приближенное решение системы. Схема алгоритма показана на рисунке 31. Пример. Решить задачу Коши на отрезке [0,3] с шагом 0,1
Текст программы:
procedure runge_ku (a,b:real;n,kolfun:integer;x:real;var y_1:TFunZnach); var Kf:array[1..NumFun,1..4] of real; h:real; begin h:=(b-a)/n; for i:=1 to n do begin for k:=1 to kolfun do begin Kf[k,1]:=h*f(x,y_1[k]);{f(t,y1,y2,x);} kf[k,2]:=h*f(x+0.5*h,y_1[k]+0.5*kf[k,1]);{f(met,y1+0.5*t*k1[1],y2+0.5*t*k1[1],x+0.5*t);} kf[k,3]:=h*f(x+0.5*h,y_1[k]+0.5*kf[k,2]);{f_1(met,y1+0.5*t*k1[2],y2+0.5*t*k1[2],x+0.5*t);} kf[k,4]:=h*f(x+h,y_1[k]+kf[k,3]);{f_1(met,y1+t*k1[2],y2+t*k1[2],x+t);} end; x:=x+h; for k:=1 to kolfun do y_1[k]:=y_1[k]+h/6*(kf[k,1]+2*kf[k,2]+2*kf[k,3]+kf[k,4]); еnd; end;
Рисунок 31 - Схема алгоритма метода Рунге-Кутта
Вычисления по программе привели к следующим результатам:
x=0 y1=0 y2=0 x=0,1 y1=0 y2=0,09 x=0,2 y1=0,01 y2=0,19 x=0,3 y1=0,03 y2=0,29 x=0,4 y1=0,06 y2=0,38 x=0,5 y1=0,10 y2=0,46 x=0,6 y1=0,15 y2=0,53 x=0,7 y1=0,20 y2=0,60 x=0,8 y1=0,27 y2=0,66 x=0,9 y1=0,34 y2=0,72 x=1 y1=0,41 y2=0,77 x=1,1 y1=0,49 y2=0,81 x=1,2 y1=0,58 y2=0,85 x=1,3 y1=0,67 y2=0,88 x=1,4 y1=0,76 y2=0,91 x=1,5 y1=0,86 y2=0,94 x=1,6 y1=0,96 y2=0,96 x=1,7 y1=1,06 y2=0,98 x=1,8 y1=1,17 y2=1,00 x=1,9 y1=1,27 y2=1,02 x=2 y1=1,38 y2=1,03 x=2,1 y1=1,49 y2=1,04 x=2,2 y1=1,60 y2=1,05 x=2,3 y1=1,71 y2=1,06 x=2,4 y1=1,82 y2=1,07 x=2,5 y1=1,93 y2=1,08 x=2,6 y1=2,05 y2=1,08 x=2,7 y1=2,16 y2=1,09 x=2,8 y1=2,28 y2=1,09 x=2,9 y1=2,39 y2=1,10
Варианты заданий для решения задачи Коши методом Эйлера приведены в таблице 7. Лабораторная работа №9 Решение задачи Коши Многошаговые методы
Метод Адамса (явный)
Входные параметры: a,b – интервал приближения; n – количество точек приближения; Kolfun – порядок системы; x – начальное значение Выходные параметры: y_1 – массив из kolfun чисел, содержащий приближенное решение системы. Схема алгоритма показана на рисунке 32. Пример. Решить задачу Коши на отрезке [0,3] с шагом 0,1
Текст программы:
procedure adams (a,b:real;n,kolfun:integer;x:real;var y_1:TFunZnach); var Fun:array[1..NumFun,1..4] of real; h:real; begin h:=(b-a)/n; for i:=1 to 4 do begin for k:=1 to kolfun do fun[k,i]:=f(y_1[k],x); runge_ku(a,b,1,1,x,y_1); x:=x+h; end; for i:=5 to n do
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.169.102 (0.014 с.) |




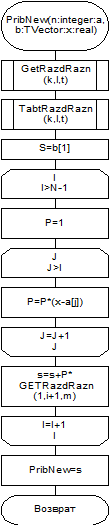

 ; y_1 – массив из kolfun чисел, содержащий начальное значение y.
; y_1 – массив из kolfun чисел, содержащий начальное значение y.