
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационные методы решений систем алгебраических уравненийСодержание книги
Поиск на нашем сайте
Точные методы
В методах Гаусса решение х находится за конечное число действий, но из-за погрешности округления и их накопления прямые методы можно назвать точными, только отвлекаясь от погрешностей округления. Метод Гаусса Прямой ход метода 1-й шаг. Предположим, что а11¹0. Поделим первое уравнение на этот элемент:
Остальные уравнений системы (1.1) запишем в виде
где i= Уравнение (1.3) умножаем на ai1 и вычитаем из i-го уравнения системы (1.4). Получим систему вида:
Система (1.5) имеет матрицу вида:
Работаем с укороченной системой, т.к. х1 входит только в 1-ое уравнение
2-й шаг. Если
Аналогично повторяем указанные действия для неизвестных х3,х4,..., хm-1 и приходим к системе с матрицей вида:
Эта матрица является верхней треугольной:
Обратный ход метода. Из последнего уравнения системы (1.6) находим хm, из предпоследнего хm-1,..., из первого уравнения – х1. Общая формула:
xm=ym/cmm,
Для реализации метода Гаусса требуется примерно (2/3)m3 арифметических операций, причем большинство из них приходится на прямой ход. Ограничение метода единственного деления заключается в том, что угловые элементы не равны нулю, т.е. Ведущие элементы –
1.1.2 Связь метода Гаусса с разложением матрицы на множители. Теорема об LU разложении.
Пусть дана система A х =B (1.1), которая при прямом ходе преобразуется в эквивалентную систему (1.6) и которую запишем в виде C х = y, (1.7) где С – верхняя треугольная матрица с единицами на главной диагонали.
Как связаны в системе (1.1) элементы В и элементы y из (1.7)?
Если внимательно посмотреть на прямой ход метода Гаусса, то можно увидеть, что
Для произвольного j имеем
где j=
Это можно записать в виде:
В=D y, где D -нижняя треугольная матрица с элементами
В связи с тем, что в методе Гаусса угловые коэффициенты не равны нулю D´C x =B. (1.9)
В результате использования метода Гаусса, получили разложение матрицы А на произведение двух матриц A = D´C, где D - нижняя треугольная матрица, у которой элементы на главной диагонали не равны нулю, а C - верхняя треугольная матрица с единичной диагональю. Таким образом, если задана матрица A и вектор B, то в методе Гаусса сначала производится разложение этой матрицы А на произведение D и C, а затем последовательно решаются две системы:
D y =B, C x = y. (1.10)
Из последней системы находят искомый вектор x. При этом разложение матрицы А на произведение СD – есть прямой ход метода Гаусса, а решение систем (1.10) обратный ход. Обозначим нижнюю треугольную матрицу через L, верхнюю треугольную матрицу - U.
Теорема об LU разложении
Введем обозначения:
Теорема. Пусть все угловые миноры матрицы А не равны нулю (Δj¹0 для j=
Идея доказательства. Рассмотрим матрицу А второго порядка и будем искать разложение этой матрицы в виде L и U.
Сопоставляя эти два равенства, определяем элементы матриц L и U (перемножим и приравняем неизвестные). Система имеет единственное решение. Методом математической индукции сказанное можно обобщить для матрицы размерности m´m. Следствие. Метод Гаусса (схема единственного деления) можно применять только в том случае, когда угловые миноры матрицы А не равны нулю.
1.1.3 Метод Гаусса с выбором главного элемента
Может оказаться так, что система (1.1) имеет единственное решение, хотя какой либо из миноров матрицы А равен нулю. Заранее неизвестно, что все угловые миноры матрицы А не равны нулю. Избежать этого можно с выбором главного элемента.
1. Выбор главного элемента по строке, т.е. производится перенумерация неизвестных системы.
ПРИМЕР. Пусть дана система второго порядка
при ½ а12 ½>½ а11 ½, тогда на первом шаге вместо неизвестного х1 исключают х2:
К этой системе применяем первый шаг прямого хода метода Гаусса. 2. Выбор главного элемента по столбцу. Предположим, что ½ а21 ½>½ а11 ½и переставим уравнения
и применяем первый шаг прямого хода метода Гаусса. Здесь имеет место перенумерация строк. 3. Поиск главного элемента по всей матрице заключается в совместном применении методов 1 и 2. Всё это приводит к уменьшению вычислительной погрешности.
1.1.4 Метод Холецкого (метод квадратных корней)
Пусть дана система
А х =В, (1.11)
где матрица А - симметричная матрица. Тогда решение системы (1.11) проводится в два этапа: 1. Симметричная матрица А представляется как произведение двух матриц
А = L * LТ.
Рассмотрим метод квадратных корней на примере системы 4-го порядка:
Перемножаем матрицы в левой части разложения и сравниваем с элементами в левой части:
2. Решаем последовательно две системы
L y =B, LT x = у.
Особенности. 1) Под квадратным корнем может получиться отрицательное число, следовательно в программе необходимо предусмотреть использование правил действия с комплексными числами. 2) Возможно переполнение - если угловые элементы близки к нулю.
Рассмотрим систему
A x= B,
где А - невырожденная действительная матрица. Метод простых итераций
Систему (3.1) преобразуем к следующему эквивалентному виду:
Или в векторной форме
Пусть задано начальное приближение
3.1.1 Условия сходимости метода.
Пусть j '(x) - матрица Якоби (якобиан), соответствующая системе (3.4) и в некоторой D-окрестности решения х функции
где (0 £ q < 1), q - постоянная.
Тогда независимо от выбора х(0) из D-окрестности корня итерационная последовательность {хk} не выходит за пределы данной окрестности, метод сходится со скоростью геометрической прогрессии и справедлива оценка погрешности
3.1.2 Оценка погрешности.
В данной окрестности решения системы, производные функции ji(x) (i=1,…,m) должны быть очень малы по абсолютной величине, т.е. сами функции должны быть почти постоянными. Тогда исходную систему (3.1) следует преобразовать к виду (3.3) с учетом условий сходимости. Пример. Рассмотрим предыдущий пример и приведем систему к удобному для итераций виду
Проверяем условие сходимости вблизи точки С. Вычислим матрицу Якоби
Так как x1»3.8, x2»2, то при этих значениях вычисляем норму матрицы
||
Запишем итерационную процедуру
Следовательно, метод простых итераций будет сходиться со скоростью геометрической прогрессии, знаменатель которой q»0.815. Вычисления поместим в таблице 1.
Таблица 1 Решение системы нелинейных уравнений
При К=9 критерий окончания счета выполняется при e=10-3 и можно положить x1 =3.774 x2 =2.077 Метод Ньютона
Суть метода состоит в том, что система нелинейных уравнений сводится к решению систем линейных алгебраических уравнений. Пусть дана система (3.1) и задано начальное приближение x (0), приближение к решению х строим в виде последовательности В исходной системе (3.1) каждую функцию
Для каждого уравнения получаем
В матричной форме
где f ' - матрица Якоби.
Предположим, что матрица не вырождена, то есть существует обратная матрица Тогда система (3.6) имеет единственное решение, которое и принимается за очередное приближение x (n+1). Отсюда выражаем решение x (n+1) по итерационной формуле:
Сходимость метода
Теорема. Пусть в некоторой окрестности решения х системы (3.1) функции fi (при i=
где n - номер итерации. Метод Ньютона сходится с квадратичной скоростью. На практике используется следующий критерий остановки:
Прямые методы 4.1.1 Метод Леверрье
Метод разделяется на две стадии: - раскрытие характеристического уравнения, - нахождение корней многочлена.
Пусть det(A-lE) - есть характеристический многочлен матрицы А ={aij} (i,j=1,2,…,m), т.е. Рассмотрим суммы вида
где В этом случае при k£m справедливы формулы Ньютона для всех (1£k£ m)
Откуда получаем
Следовательно, коэффициенты характеристического многочлена р i можно определить, если известны суммы S1,S2,...,Sm. Тогда схема алгоритма раскрытия характеристического определителя методом Леверрье будет следующей: 1) вычисляем степень матрицы: Ак=Ак-1*А для k=1,…,m; 2) определяют Sk - суммы элементов стоящих на главной диагонали матриц Ак;
3) по формулам (4.5) находят коэффициенты характеристического уравнения рi (i=1,2,…,m). 4.1.2 Усовершенствованный метод Фадеева
Алгоритм метода: 1) вычисляют элементы матриц A1,A2,..,Am:
(в конце подсчета Bm нулевая матрица для контроля);
2) определяют коэффициенты характеристического уравнения рi q1 = -р1, q2 = -р2,..., qm = -рm. Существуют и другие методы раскрытия характеристического определителя: метод Крылова, Данилевского и др.
4.1.3 Метод Данилевского Две матрицы A и B называются подобными, если одна получается из другой путем преобразования с помощью некоторой не вырожденной матрицы S:
B=S-1*AS,
если это равенство справедливо, то матрицы A и B подобны, а само преобразование называется преобразованием подобия (переход к новому базису в пространстве m - мерных векторов). Пусть y - результат применения матрицы A к вектору х
y =A* х.
Сделаем замену переменных:
x =S* x ', y =S* y'.
Тогда равенство y =A* х преобразуется к виду
y' =S-1*A*S* x'.
В этом случае матрица B и матрица A имеют одни и те же собственные числа. Это можно легко увидеть раскрыв определитель
Следовательно, матрицы A и B - подобные, имеют одни и те же собственные значения. Но собственные векторы х и х’ – не совпадают, они связаны между собой простым соотношением
х = S* х '.
Такую матрицу A с помощью преобразования подобия или же последовательности таких преобразований можно привести к матрице Фробениуса вида:
Детерминант матрицы F det (F) можно разложить по элементам первой строки:
Тогда коэффициенты характеристического многочлена матрицы А будут р1 = f11 , p2 = f12,…, pn = f1m.
Второй случай. Матрицу А преобразованием подобия можно привести к матрице В верхнего треугольного вида
Тогда собственными числами будут диагональные элементы матрицы B:
Третий случай. Матрицу A с помощью преобразования подобия можно привести к Жордановой форме
где li - собственные числа матрицы A; Si - константы (0 или 1); если Si=1, то li=li+1.
К четвёртому случаю относятся матрицы, которые с помощью преобразования подобия можно привести к диагональному виду (матрица простой структуры):
Задача приближения функции
Постановка задачи. Пусть на отрезке [a,b] задана функция у= f(x) своими n+1 значениями Допустим, что вид функции f(x) неизвестен. На практике часто встречается задача вычисления значений функции у= f(x) в точках х, отличных от Определение. Точки Требуется найти аналитическое выражение функции F(x), совпадающей в узлах интерполяции со значениями данной функции, т.е.
Определение. Процесс вычисления значений функции F(x) в точках отличных от узлов интерполирования называется интерполированием функции f(x). Если
Геометрически задача интерполирования функции одной переменной означает построение кривой, проходящей через заданные точки
x
Рисунок 5 - Геометрическая иллюстрация задачи интерполирования функции
Задача становится однозначной, если в качестве F(x) выбрать многочлен степени не выше n, такой что:
F
Определение. Многочлен F Определение. Когда многочлен F(x) выбирается в классе степенных функций, то интерполяция называется параболической. Знание свойств функции f позволяет осознанно выбирать класс G аппроксимирующих функций. Широко используется класс функций вида
являющихся линейными комбинациями некоторых базисных функций
Фm(хi)=yi, (i=0,1,…,n). (5.2)
Покажем, что условие (5.2) позволяет найти приближающую функцию единственным образом
Система (5.3) есть система линейных алгебраических уравнений относительно коэффициентов с0,с1,…,сm. Эта система n линейных уравнений имеет единственное решение, если выполняется условие m=n и определитель квадратной матрицы Р
Определение. Система функций Пример. При m£n система функций 1 ,х,х2,…,хm линейно независима в точках х0,х1,…,хn, если они попарно различны. Отсюда следует, что
где знаменатель не должен быть равен нулю, т. е.
Если условие (6.47) выполнено, то краевая задача (6.35), (6.36) имеет единственное решение. Если же (6.47) не выполняется, то краевая задача (6.35), (6.36) либо не имеет решения, либо имеет бесконечное множество решений.
Задано начальное условие
и заданы краевые условия первого рода
Требуется найти функцию u(x,t), удовлетворяющую в области D (0< x
При проведении замены Приближенное значение искомой функции в точке j =0,1,..., m;
В результате получим неявную двухслойную схему с погрешностью O(t+h2)
Используя подстановку
где: u0,j=m1 (tj); un,j=m2 (tj). Получаем разностную схему, которой аппроксимируем уравнение (7.4). Эта схема (7.7) неявная, и выглядит так, как показано на рисунке 10. При построении схемы (7.7) получается система линейных уравнений с трехдиагональной матрицой. Решив ее любым способом (в частности, методом прогонки), получаем значения функции на определенных временных слоях. Так, на нулевом временном слое используем начальное условие Ui,0=f (xi), т.к. j =0. Эта неявная схема более устойчива для любых значений параметра l>0. Есть и явная схема (рисунок 11), но она устойчива только при
Рисунок 11 - Явная схема Лабораторная работа № 1 Варианты заданий
Таблица 2
Лабораторная работа № 3 Лабораторная работа № 4 Лабораторная работа № 5 Точные методы Метод Леверрье
Входные параметры: n—целое положительное число, равное порядку n системы; Выходные параметры: b—массив из n действительных чисел, при выходе из программы содержит решение системы. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE Liver (Var VeS:Tvector;Nn:Integer);; Label 35,270,220,100,80,190,500,250,350,120,10; Var I,J,K,T:Integer; Y,Yy:tvector; {A,Aa:Mas;} S,C,Q,P,H,D,U,M,V,F,W,Yyy,Z,L,R,X,Aaa,B:Real; Sq,Sq1: Real; F1: TEXT; Begin Assign(F1,'last.out'); Rewrite(F1); For I:=Nn Downto 1 Do Y[i+1]:=VeS[i]; Y[1]:=1; K:=1; 35: T:=1; C:=Y[2]/Y[1]; If (Nn=1) Then Begin P:=-C; Q:=0; Goto 270; End; If (Nn=2) Then Begin H:=C*C/4-Y[3]/Y[1]; Goto 220; End; M:=10;C:=4;D:=8;U:=4; V:=8;F:=1;W:=2;T:=0; 80: If(M<>10) Then Goto 100; P:=C;M:=0;Q:=D;C:=U;D:=V; U:=P;V:=Q;Yyy:=C;Z:=D;F:=-F; 100:M:=M+1;H:=0;Q:=Y[1];P:=Y[2]-C*Q;L:=Q; 120:For J:=3 To Nn Do Begin R:=P;P:=Y[j]-C*R-D*Q;Q:=R; R:=L;L:=Q-C*R-H*D;H:=R; End; Q:=Y[Nn+1]-D*Q; S:=L+C*R; If (T=0) Then Begin X:=D*R;H:=R*X+S*L; If H=0 Then Goto 80; End; C:=C+(P*S-Q*R)/H; D:=D+(P*X+Q*L)/H; If ((C-Yyy+D-Z)<>0) Then Goto 190; If (F=-W) Then Begin writeln('Љ®аҐм Ґ ©¤Ґ'); Goto 500; End; W:=-F; 190:H:=C*C/4-D; Sq:=Sqrt((Q-P*C/2)*(Q-P*C/2)+P*P*Abs(H)); If (Sq>0.0000001) Then Goto 80; T:=0; Y[2]:=Y[2]-C*Y[1]; For J:=3 To Nn-1 Do Begin Y[j]:=Y[j]-C*Y[j-1]-D*Y[j-2];End; 220:P:=-C/2; Q:=Sqrt(Abs(H)); If(h>=0) Then Begin M:=P+Q;P:=P-Q;Q:=0; Goto 250; End; M:=P; 250:write(F1,'p',k,'=',m:9:4,' + i',q:7:4);K:=K+1;{Ves[k-1]:=M;}WriteLn(F1,''); 270:write(F1,'p',k,'=',p:9:4,' + i',-q:7:4);K:=K+1;{Ves[k-1]:=P;}WriteLn(F1,''); If(t<>0) Then Goto 350; Nn:=Nn-2; Aaa:=0; Sq1:=Sqrt((S-R*C/2)*(S-R*C/2)+R*R*Abs(H)); If (Sq1<=0.0000001) Then Aaa:=1; B:=0; If (Nn>=2) Then B:=1; If((Aaa+B)=2) Then Begin T:=1; Goto 120; End; Goto 35;350:500: Close(F1); End;
Вычисления по программе привели к следующим результатам: Собственные числа Собственные вектора .10000Е+01 -.94281Е+00.23570Е+00 -.23570Е+00 .10000Е+02 -.33333Е+00 -.66667Е+00.66667Е+00 .10000Е+01.00000Е+00 -.70711Е+00 -.70711Е+00
Варианты заданий для нахождения собственных значений и собственных векторов матрицы приведены в таблице 5. Метод Фадеева
Входные параметры: n—целое положительное число, равное порядку n системы; а — массив из n х n действительных чисел, содержащий входную матрицу. Выходные параметры: q—массив из n действительных чисел при выходе из программы содержит решение системы. Метод Крылова
Входные параметры: n—целое положительное число, равное порядку n системы; а — массив из n х n действительных чисел, содержащий входную матрицу. Выходные параметры: q—массив из n действительных чисел при выходе из программы содержит решение системы. Схема алгоритма приведена на рисунке 24. Пример. Вычислить собственные значения и собственные вектора матрицы
|2 2 –2| |2 5 –4| |-2 –4 5|
Текст программы:
PROCEDURE Krylov(Nn:integer; A: TMatr;Var Y:TVector); Label 2; Var I,J,K,T,Nn1:Integer; yy:TVector; aa:TMatr; s,c,q,p,h,d,u, m,v,f,w,yyy,z, l,r,x,aaa,b: Real; Begin form3.Caption:='Крылов'; Nn1:=Nn; For I:=1 To Nn Do Yy[i]:=I*Trunc(10*ranDom); 2:For I:=Nn Downto 1 Do Begin Y:=Yy; For J:=1 To Nn Do Aa[j,i]:=Yy[j]; For J:=1 To Nn Do Begin S:=0; For K:=1 To Nn Do S:=S+A[j,k]*Y[k]; Yy[j]:=S; End; End; For I:=1 To Nn Do Y[i]:=-Yy[i]; Simq(Nn1,Aa,Y,K
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.90.203 (0.011 с.) |

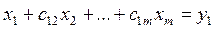 . (1.3)
. (1.3) , (1.4)
, (1.4) .
. . (1.5)
. (1.5) .
. .
. .
. , то из укороченной системы аналогично исключаем неизвестное x2 и получаем матрицу коэффициентов такого вида:
, то из укороченной системы аналогично исключаем неизвестное x2 и получаем матрицу коэффициентов такого вида: .
. . (1.6)
. (1.6) .
. , (i=m-1,…,1).
, (i=m-1,…,1). .
.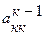 – элементы на k-ом шаге исключения. Но если ведущий элемент близок к нулю, то в процессе вычисления может накапливаться погрешность. В этом случае на каждом шаге исключают не хk, a хj (при j¹k). Такой подход называется методом выбора главного элемента. Для этого выбирают неизвестные xj с наибольшим по абсолютной величине коэффициентом либо в строке, либо в столбце, либо во всей матрице. Для его реализации требуется
– элементы на k-ом шаге исключения. Но если ведущий элемент близок к нулю, то в процессе вычисления может накапливаться погрешность. В этом случае на каждом шаге исключают не хk, a хj (при j¹k). Такой подход называется методом выбора главного элемента. Для этого выбирают неизвестные xj с наибольшим по абсолютной величине коэффициентом либо в строке, либо в столбце, либо во всей матрице. Для его реализации требуется  - арифметических действий.
- арифметических действий. .
. , (1.7)
, (1.7) , dji – числовые коэффициенты:
, dji – числовые коэффициенты: . (1.8)
. (1.8) на главной диагонали (j=
на главной диагонали (j=  ,
,  ).
). , то на главной диагонали матрицы D стоят не нулевые элементы. Следовательно, эта матрица имеет обратную, тогда y=D-1В, С x = D-1В. Тогда
, то на главной диагонали матрицы D стоят не нулевые элементы. Следовательно, эта матрица имеет обратную, тогда y=D-1В, С x = D-1В. Тогда - угловой минор порядка j матрицы А, т.е.
- угловой минор порядка j матрицы А, т.е.
 .
.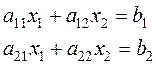
 .
.
 .
.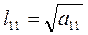 ,
,  ,
,  ,
,  ,
,  ,
,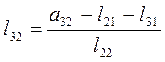 ,
,  ,
,  .
.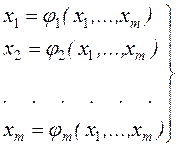 .
.

 . Подставляем его в правую часть системы (3.4) и получаем x(1)=j(x(0)), продолжая подстановку, находим х(2) и т.д. Получим последовательность точек
. Подставляем его в правую часть системы (3.4) и получаем x(1)=j(x(0)), продолжая подстановку, находим х(2) и т.д. Получим последовательность точек 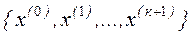 , которая приближается к исходному решению х.
, которая приближается к исходному решению х. (i=1,2,…,m) дифференцируемы и выполнено неравенство вида:
(i=1,2,…,m) дифференцируемы и выполнено неравенство вида: ,
, .
.
 .
.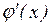
 ||»0.815.
||»0.815.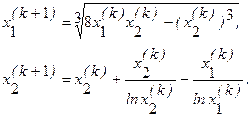



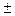 0.001
0.001 .
. где i=
где i=  .
.
 .
.

 .
. .
.
 ,
, .
. , и l1,l2,…,lm - есть полная совокупность корней этого многочлена (полный спектр собственных значений).
, и l1,l2,…,lm - есть полная совокупность корней этого многочлена (полный спектр собственных значений).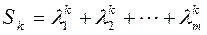 (k=1,2,…,m), т.е.
(k=1,2,…,m), т.е. ,
,
 - след матрицы.
- след матрицы. ,
,

 .
. .
. .
. .
. .
.
 ,
, ,
,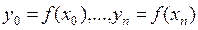 , в точках
, в точках  .
. . Кроме того, в некоторых случаях, не смотря на то, что аналитическое выражение у=f(x) известно, оно может быть слишком громоздким и неудобным для математических преобразований (например, специальные функции). Кроме этого значения yi могут содержать ошибки эксперимента.
. Кроме того, в некоторых случаях, не смотря на то, что аналитическое выражение у=f(x) известно, оно может быть слишком громоздким и неудобным для математических преобразований (например, специальные функции). Кроме этого значения yi могут содержать ошибки эксперимента.
 , то задача вычисления приближенного значения функции в т. х называется интерполированием, иначе - экстраполированием.
, то задача вычисления приближенного значения функции в т. х называется интерполированием, иначе - экстраполированием. (рисунок 5). То есть задача в такой постановке может иметь бесконечное число решений.
(рисунок 5). То есть задача в такой постановке может иметь бесконечное число решений. у
у


 x
x  x
x  x
x  х
х (x
(x  (5.1)
(5.1)
 ,...,с
,...,с  , которые находятся в зависимости от вида приближения. Функцию Фm(х) называют обобщенным многочленом по системе функций j0(х),j1(х),…,jm(х), а число m – его степенью. Назовем обобщенный многочлен Фm(х) интерполяционным, если он удовлетворяет условию
, которые находятся в зависимости от вида приближения. Функцию Фm(х) называют обобщенным многочленом по системе функций j0(х),j1(х),…,jm(х), а число m – его степенью. Назовем обобщенный многочлен Фm(х) интерполяционным, если он удовлетворяет условию
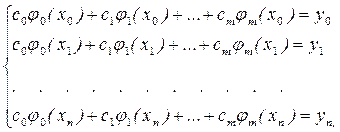 (5.3)
(5.3)
 ,
, .
.

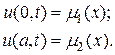
 a, 0< t
a, 0< t  T) условиям (7.5) и (7.6). Физически это можно представить как стержень, на концах которого поддерживается требуемый температурный режим, заданный условиями (7.6).
T) условиям (7.5) и (7.6). Физически это можно представить как стержень, на концах которого поддерживается требуемый температурный режим, заданный условиями (7.6). Рисунок 10 – Неявная схема
Рисунок 10 – Неявная схема
 получим
получим  , т.е. k =1. Задача решается методом сеток: строим в области D равномерную сетку с шагом h по оси x и шагом t по t (см. рисунок 10).
, т.е. k =1. Задача решается методом сеток: строим в области D равномерную сетку с шагом h по оси x и шагом t по t (см. рисунок 10). -
-  обозначим через
обозначим через  . Тогда
. Тогда  ;
;  ; i =0,1,..., n;
; i =0,1,..., n;  ;
; .
. ;
; .
. .
.
 , выразим из этой схемы ui,j-1
, выразим из этой схемы ui,j-1 ,
,
 , т.е. при
, т.е. при  .
.



