
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краевые задачи для обыкновенных дифференциальных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Постановка краевой задачи. Рассматриваем дифференциальное уравнение порядка n (n³ 2)
где: Если сделаем замену переменных вида
то задача (6.35) сводится к задаче Коши для нормальной системы ОДУ порядка n. Типовые примеры краевых задач. Рассмотрим теперь дифференциальное уравнение
Для уравнения (6.37) краевая задача формулируется следующим образом: найти решение y=y(x), удовлетворяющее уравнению (6.37), для которой значения ее производных в заданной системе точек
1. Рассмотрим уравнение второго порядка
2. Рассмотрим уравнение Из графика на рисунке 8 видно, что tg(a)=A1 , tg(b)=B1. Здесь интегральная кривая пересекает прямые x=a и x=b под заданными углами a и b соответственно. 3. Смешанная краевая задача. Рассмотрим то же самое уравнение Замечание. Краевая задача для уравнения (6.37) в общем случае может не иметь решений, иметь единственное решение, иметь несколько решений или бесконечное множество решений. 4. Поражение заданной цели баллистическим снарядом. Дифференциальные уравнения движения снаряда с учетом сопротивления воздуха имеют вид
где: Предполагая, что при t=t0 снаряд выпущен из точки, совпадающей с началом координат с начальной скоростью v0 под углом Q0, а в момент t=t1 поразит неподвижную мишень в точке
Здесь неизвестны Q0 и t1. Решив данную краевую задачу, можем найти начальный угол
Решение линейной краевой задачи
Рассмотрим важный частный случай решения краевой задачи, когда дифференциальное уравнение и краевые условия линейны. Для этого рассмотрим уравнение
где: Предположим, что в краевые условия входят две абсциссы x=a, x=b. Это двухточечные краевые задачи. Краевые условия называются линейными, если они имеют вид
где: a, b, g -заданные константы. Причем они одновременно не равны нулю, т.е.
Например, краевые условия во всех трех рассмотренных ранее задачах линейны, т.к. их можно записать в виде
причем Решение двухточечной краевой задачи для линейного уравнения второго порядка сведением к задаче Коши
Запишем линейное уравнение второго порядка в виде
где: p, q, f -известные непрерывные функции на некотором отрезке [a,b]. Требуется найти решение уравнения (6.40), удовлетворяющее заданным краевым условиям
Причем константы a и b одновременно не равны нулю
Решение задачи (6.40), (6.41) будем искать в виде линейной комбинации
y=C×u+V,
где С - константа, u -общее решение соответствующего однородного уравнения
а V -некоторое частное решение неоднородного уравнения
Потребуем,чтобы первое краевое условие было выполнено при любом C,
откуда следует, что Тогда
где k - некоторая константа, не равная нулю. Значение функции V и ее производная в точке а
если коэффициент
если коэффициент Из этих рассуждений следует, что функция u - есть решение задачи Коши для однородного уравнения (6.42) с начальными условиями (6.44), а функция V - есть решение задачи Коши для неоднородного уравнения (6.43) с начальными условиями (6.45) или (6.46) в зависимости от условий. Константу C надо подобрать так, чтобы выполнялись условия (6.41) (вторая строчка) в точке x=b
Отсюда следует, что
где знаменатель не должен быть равен нулю, т. е.
Если условие (6.47) выполнено, то краевая задача (6.35), (6.36) имеет единственное решение. Если же (6.47) не выполняется, то краевая задача (6.35), (6.36) либо не имеет решения, либо имеет бесконечное множество решений.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

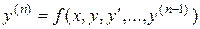 ,
,
 ; к =0,1,…,(n -1).
; к =0,1,…,(n -1).
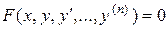 .
.
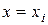 удовлетворяют n независимым краевым условиям, в общем виде нелинейным. Эти краевые условия связывают значения искомой функции y и ее производных до (n -1) порядка на границах заданного отрезка.
удовлетворяют n независимым краевым условиям, в общем виде нелинейным. Эти краевые условия связывают значения искомой функции y и ее производных до (n -1) порядка на границах заданного отрезка. Рисунок 7 – Краевые условия для случая 1
Рисунок 7 – Краевые условия для случая 1
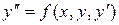 . Необходимо найти решение уравнения, удовлетворяющее заданным краевым условиям: y(a)= A, y(b)= B, т.е. необходимо найти интегральную кривую, проходящую через две заданные точки (рисунок 7).
. Необходимо найти решение уравнения, удовлетворяющее заданным краевым условиям: y(a)= A, y(b)= B, т.е. необходимо найти интегральную кривую, проходящую через две заданные точки (рисунок 7). Рисунок 8 – Краевые условия для случая 2
Рисунок 8 – Краевые условия для случая 2
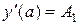 ,
,  .
. ,
, Рисунок 9 – Траектория снаряда
Рисунок 9 – Траектория снаряда
 - вторая производная по времени; E=E(y,v) -известная функция высоты и скорости;
- вторая производная по времени; E=E(y,v) -известная функция высоты и скорости;  ; g=g(y) - ускорение силы тяжести;
; g=g(y) - ускорение силы тяжести; 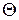 -угол наклона к горизонту касательной к траектории движения снаряда;
-угол наклона к горизонту касательной к траектории движения снаряда;  .
. получаем краевые условия
получаем краевые условия
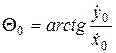 , где:
, где: 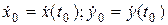 ; Q0 -угол, при котором поражается цель в точке M.
; Q0 -угол, при котором поражается цель в точке M. ,
,
 и f(x) известные непрерывные функции на отрезке [a, b].
и f(x) известные непрерывные функции на отрезке [a, b]. =g,
=g,
 , при v =1,2,…, n.
, при v =1,2,…, n.
 ,
,
 - для первой задачи.
- для первой задачи. ,
,


 ,
,
 .
.
 ,
,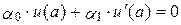 ,
,  .
. ,
,
 ,
,
 ¹0 и
¹0 и ,
,
 ¹0.
¹0. .
. ,
, .
.



