
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение дифференциальных уравнений в частных производныхСодержание книги
Поиск на нашем сайте
В реальных физических процессах искомая функция зависит от нескольких переменных, а это приводит к уравнениям в частных производных от искомой функции. Как и в случае обыкновенных дифференциальных уравнений(ОДУ), в этом случае для выбора одного конкретного решения, удовлетворяющего уравнению в частных производных, необходимо задавать дополнительные условия (т.е. краевые условия). Чаще всего такие задачи на практике не имеют аналитического решения и приходится использовать численные методы их решения, в том числе метод сеток, метод конечных разностей и так далее. Мы будем рассматривать класс линейных уравнений в частных производных. В общем виде эти уравнения записываются в виде
где: A, B, C, a, b, c -заданные непрерывные функции двух переменных, имеющие непрерывные частные производные, u -искомая функция. Для сокращения записи введем обозначения
Будем рассматривать упрощенную форму записи (7.1) вида
и рассмотрим частный случай (7.2), когда a=b=c=F º0, т.е.
Путем преобразований уравнение (7.3) может быть приведено к каноническому виду (к одному из трех стандартных канонических форм) эллиптическому типу, гиперболическому типу, параболическому типу. Причем тип уравнения будет определяться коэффициентами А, В, С, а именно – знаком дискриминанта
D=B2- 4 ×A×C.
Если D <0, то имеем уравнение эллиптического типа в точке с координатами x, y; если D =0, то (7.3)-параболического типа; если D >0, то (7.3)-гиперболического типа; если D не сохраняет постоянного знака, то (7.3)-смешанного типа.
Замечание. Если А, В, С - константы, тогда каноническое уравнение (7.3) называется полностью эллиптического, параболического, гиперболического типа. Введем понятие оператора Лапласа для сокращенной записи канонических уравнений вида
Используя это определение, запишем сокращенные канонические уравнения всех трех типов 1. D u =0. Это уравнение эллиптического типа, так называемое уравнение Лапласа. В механике это уравнение описывает стационарные тепловые поля, установившееся течение жидкости и т.д. 2.D u =- f, где f -заданная непрерывная функция. Это уравнение Пуассона имеет эллиптический тип и описывает процесс теплопередачи с внутренним источником тепла.
3. 4.
7.1 Метод сеток для решения смешанной задачи для уравнения параболического типа (уравнения теплопроводности)
Смешанная задача означает, что следует найти искомую функцию, удовлетворяющую заданному уравнению в частных производных, краевым, а так же начальным условиям. Рассмотрим смешанную задачу для однородного уравнения теплопроводности
Задано начальное условие
и заданы краевые условия первого рода
Требуется найти функцию u(x,t), удовлетворяющую в области D (0< x
При проведении замены Приближенное значение искомой функции в точке j =0,1,..., m;
В результате получим неявную двухслойную схему с погрешностью O(t+h2)
Используя подстановку
где: u0,j=m1 (tj); un,j=m2 (tj). Получаем разностную схему, которой аппроксимируем уравнение (7.4). Эта схема (7.7) неявная, и выглядит так, как показано на рисунке 10. При построении схемы (7.7) получается система линейных уравнений с трехдиагональной матрицой. Решив ее любым способом (в частности, методом прогонки), получаем значения функции на определенных временных слоях. Так, на нулевом временном слое используем начальное условие Ui,0=f (xi), т.к. j =0. Эта неявная схема более устойчива для любых значений параметра l>0. Есть и явная схема (рисунок 11), но она устойчива только при
Рисунок 11 - Явная схема
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.61 (0.01 с.) |


 ,
,
 ;
; 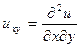 ;
;  ;
;  ;
;  .
.
 .
.
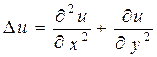 .
.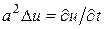 , где a -константа. Не во всех уравнениях в качестве переменных будут выступать стандартные переменные x, y. Может быть также переменная времени. Это уравнение диффузии описывает процесс теплопроводности и является уравнением параболического типа.
, где a -константа. Не во всех уравнениях в качестве переменных будут выступать стандартные переменные x, y. Может быть также переменная времени. Это уравнение диффузии описывает процесс теплопроводности и является уравнением параболического типа.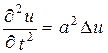 , а -константа. Это уравнение гиперболического типа - так называемое волновое уравнение и оно описывает процесс распространения волн.
, а -константа. Это уравнение гиперболического типа - так называемое волновое уравнение и оно описывает процесс распространения волн. , k =const>0.
, k =const>0.

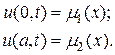
 a, 0< t
a, 0< t  T) условиям (7.5) и (7.6). Физически это можно представить как стержень, на концах которого поддерживается требуемый температурный режим, заданный условиями (7.6).
T) условиям (7.5) и (7.6). Физически это можно представить как стержень, на концах которого поддерживается требуемый температурный режим, заданный условиями (7.6). Рисунок 10 – Неявная схема
Рисунок 10 – Неявная схема
 получим
получим  , т.е. k =1. Задача решается методом сеток: строим в области D равномерную сетку с шагом h по оси x и шагом t по t (см. рисунок 10).
, т.е. k =1. Задача решается методом сеток: строим в области D равномерную сетку с шагом h по оси x и шагом t по t (см. рисунок 10). -
-  обозначим через
обозначим через  . Тогда
. Тогда  ;
;  ; i =0,1,..., n;
; i =0,1,..., n;  ;
; .
. ;
; .
. .
.
 , выразим из этой схемы ui,j-1
, выразим из этой схемы ui,j-1 ,
,
 , т.е. при
, т.е. при  .
.



