
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрические уравнения прямой на плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Параметрические уравнения прямой на плоскости. Пусть в афинной системе координат (0, X, Y) задана прямая l, ее направляющий вектор
и так как Если обозначить - радиус-векторы соответственно точек M иM0, то параметрическое уравнение прямой. Отсюда следует, что
Вычисление расстояния отточки до прямой. Расстояние d от точки М0 до прямой l есть длина перпендикуляра, проведенного из точки М0 к прямой. Пусть задана прямоугольная система координат Оху. Тогда отклонением точки М0(х0,у0) от прямой ax+by+c=0, a2+b2≠0 называется величина Расстояние от точки М0(х0,у0) до прямой ax+by+c=0 вычисляется по формуле Приведение общего уравнения прямой к нормированному виду. Если обе части уравнения Ах + Ву + С = 0 разделить на число xcosφ + ysinφ - p = 0 – нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ? С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох. Пучок прямых. Пучком прямых на плоскости наз. совокупность прямых, проходящих через фиксированную точку – центр пучка. Пусть ур. a1x+b1y+c1=0 a2x+b2y+c2=0, задают две различные параллельные прямые, пересекающиеся в точке S. Множество всех прямых, проходящих через точку S, наз. пучком прямых. Уравнение a1x+b1y+c1+λ(a2x+b2y+c2)=0 задаёт некоторую прямую пучка и, обратно: любая прямая пучка, отличная от прямой a2x+b2y+c2=0, может быть задана ур. a1x+b1y+c1+λ(a2x+b2y+c2)=0. Общее уравнение плоскости. В прямоугольной декартовой декартовой системе координат Ох,у,z любая плоскость определяется уравнением вида ax+by+cz+d=0, где коэффициенты при неизвестных а,в,с одновременно неравны нулю и явл. координатами нормального вектора n=( a,b,c ). Общее ур. наз. полным, если все ко-ты отличны от нуля. Неполные ур. показывают особенности расположения плоскости в системе. Неполные уравнения. Если в общем уравнении прямой один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:
1). С=0; уравнение имеет вид и определяет прямую, проходящую через начало координат. 2). В=0; уравнение имеет вид и определяет прямую, перпендикулярную к оси Ох. 3). В=0, С=0; уравнение может быть записано в виде х=0 и определяет ось ординат. 4). А=0; уравнение имеет вид и определяет прямую, перпендикулярную к оси Оу 5). А=0, С=0 уравнение может быть записано в виде у=0 и определяет ось абсцисс. Уравнение плоскости по трем точкам. Пусть даны три точки М1(x1,y1,z1), М2(x2,y2,z2), М3(x3,y3,z3). Через три точки плоскость и только одна.
Векторы М1М, М1М2, М1М3 – комплонарны, поэтому по признаку комплонарности их смешанное произведение равно нулю. Этот определитель представляет ур.плоскости по трем её точкам. 51.Уравнение плоскости "в отрезках".
Параметрические уравнения плоскости. В векторном виде В координатах Расстояние от точки до плоскости. Пусть М0(x0,y0,z0) и плоскость заданы общим ур. ax+by+cz+d=0. Расстояние от точки до плоскости находится также, как расстояние от точки до прямой на плоскости. Т. Расстояние от точки М0(x0,y0,z0) до плоскости ax+by+cz+d=0 вычисляется по формуле Приведение общего уравнения плоскости к нормированному.
Пучок плоскостей. Совокупность всех плоскостей проходящих через одну и туже прямую l наз. пучком плоскостей с центром l. Т. Пусть a1x+b1y+c1z+d1=0 и a2x+b2y+c2z+d2=0 уравнения двух плоскостей пересекающихся по прямой l. Для любых действительных чисел 𝛂 и 𝛃 неравных нулю уравнение 𝛂(a1x+b1y+c1z+d1)+𝛃(a2x+b2y+c2z+d2)=0(*) определяет плоскость проходящую через прямую l и, обратно: всякая плоскость проходящая через l определяется ур.(*) при подходящих значениях 𝛂 и 𝛃.
57.Связка плоскостей.
Т. При любых ко-тах а,в,с неравных одновременно неравных нулю ур. вида a(x-x0)+b(y-y0)+c(z-z0)=0(*) определяет плоскость проходящую через точку М0(x0,y0,z0) и, обратно: любое ур. вида(*)определяет плоскость проходящую через точку М0. 58.Общие уравнения прямой в пространстве.
то система вида 59.Канонические уравнения прямой в пространстве. Пусть прямая проходит через фиксированную точку М0(x0,y0,z0) параллельно направляющему вектору q (l,m,n).
М0М коллинеарен q, поэтому их соотв. координаты пропорциональны, т.е. справедливо равенство Свойства линейных операций. 1.слож-е м-ц коммутативно, т.е А+В=В+А 2.слож-е м-ц ассоциативно,т.е (А+В)+С=А+(В+С) 3.А+0=А, где 0- нулева м-ца одинак-я с А порядка 4.Для " А $ противопол-ная м-ца -А такая, что А+(-А)=0 Св-во умножения на число: 5. 1 × А=А 6. l(bА)=(lb)А Две линейные операции связаны дистрибутивными законами 7.(a+b)А=aA+bВ 8.a(А+В)=aА+aВ Свойства определителей. 1. Каков бы ни был номер строки опр-ля, справедл. ф-ла÷А÷ =(-1)i+1 ai1Mi1+(-1)i+2 ai2Mi2+...+(-1)i+n ainMin,т.е. опр-ль разлаг-ся по кажд. своей строке.÷A÷= S (-1)i+j aijMij 2. Опр-ль разлаг-ся по кажд. j-тому ст-цу м-цы, т.е. опр-ль÷A÷ =(-1)1+j a1jM1j+(-1)2+j a2jM2j+...+(-1)n+j aijMij Опр.: М-ца Ат наз. транспонированной м-цей к м-це А, если эл-т (i,j)м-цы А явл. (i,j)-тым эл-том м-цы Ат, т.е. если эл-т аij стоит в j-том столбце и i-той стр.,то в м-це Ат этот эл-нт нах-ся в j-той стр. и i-том столбце. 3. При транспонир. кв. м-цы опр-ль не меняется, т.е. опр-ль м-цы А = опр-лю м-цы Ат. 4. При перестановке местами двух любых строк м-цы (столбц) опр-ль сохран. абсол-ую величину, но меняет знак на противоположн. Опр. Известное определен.линейной завис-ти для векторов справедливо также и для строк (столбцов) м-цы. 5. Если в м-це А i-тая строка (столбец) явл. линейной комбинац. строк В=(b1,b2,...,bn) и С=(с1,с2,...,сn) с коэф-ми a,b,то÷A÷=÷A÷+÷A2÷, где А1- м-ца, получ. из м-цы А заменой её i-той строки строкой В,а м-ца А2 получ. из м-цы А заменой её i-той стр. строкой С. 6. Если в кв. м-це есть 2 одинак. строки (столбца), то опр-ль этой м-цы =0. 7. Если строку (столбец) опр-ля умнож. на какое-то число, то опр-ль тоже умн-ся на это число. 8. Если все эл-ты какой-то стр. (столбца) = 0, то опр-ль м-цы=0. 9. Если эл-ты двух строк (столбцов) соответственно пропорц-ны, то опр-ль м-цы =0. 10. Если к эл-там некоторой строки опр-ля прибавить соотв-щие эл-ты др. строки м-цы, умнож-ные на число х, то опр-ль не изменится, то же для столбцов. Опр. Алгебраич-ким дополнением эл-та aij кв. м-цы А наз-ся число, обозн. Аij=(-1)^i+j Mij
Т-ма об алгабраич. дополнениях: Сумма произведений любой строки м-цы на соотв-щие алгебраические дополнения эл-тов др. строки этой м-цы=0 Система линейных уравнений. Основные понятия. Опр. Системой лин. алгеброич. ур-й с неизвестными х1,х2...,хn наз. совок. ур-й: a11x1+a12x2+...+a1n xn=b1 a21x2+a22x2+...+a2n xn= b2 am1x1+am2x2+...+amnxn=bn Опр. Если число ур-й совпадает с числом неизв-ых, т.е m=n, то система наз-ся квадратной Опр. Число aij, где i-номер ур-я, j-номер неизвестного наз. коэ-том при неизвестных числа b1,b2...,bm-свободным членом. Опр. Система имеющая хоты бы одно решение, наз-ся совместной, система неимеющая ни одного реш. наз. несовм. Опр. Система имеющая точно одно реш-е наз. опр-ой. Опр. Система имеющая более одного реш-я наз. неопр-ой. Опр. Две системы наз-ся эквивал-ми, если все реш-я одной из них также явл-ся реш-ями другой и обратно. Опр. Элементарными преобразованиями системы наз-ся: 1.замена местами любого ур-я системы.: 2.умножение ур-й на любые числа отличные от нуля. 3.прибав-е один одному ур-ю другого, умнож-е на любое число Опр. Прямоуг-я таблица,состоящая из коэ-тов при неизвестных системы 1 наз-ся осн-ой м-цей системы. a11 a12...a1n А= a21 a22...a2n -основная м-ца. am1 am2..amn Опр. Таблица,сост. из свободн.членов, наз-ся столбцом св.чл. Теорема Крамера. Если определитель основной матрицы квадратной линейной системы уравнений отличен от нуля, то система имеет единственное решение, которое находиться по формуле Метод Гаусса. Теорема Крамера применяектся только к кв. системам, и только в случае, когда опр-ль осн. м-цы А Метод Гаусса применяется для люб. систмы- это один из гл. методов реш-я систем. Метод Гаусса - метод последовательного исключения переменных. С пом. элементарных преобразований строк расширенной м-цы D системы приводят к ступенчатому виду м-цу А системы: c11 c12...c1r...c1n d1 c21 c22...c2r...c2n d2 ................. 0 0... crr... crn dr 0 0... 0... 0 dr+1 ................ 0 0... 0... 0 dm (ciir). если среди чисел dr+1, dr+2..., dm есть отличные от нуля, то система несовместна Если dr+1=dr+2=...= dm=0, то: 1. при r=n исходная система равносильна системе c11x1+c12x2+...+c1nxn=d1 c22x2+...+c2nxn=d2 .................. cnnxn=dn имеющей единственное реш-е (находим сначала из последнего ур-я xn, из предпоследнего xn-1 и т.д. и из первого x1) 2. при r<n исходная сист. равносильна системе c11x1+c12x2+...+c1rxr=d1-c1r+1xr+1-...-c1nxn c22x2+...+c2rxr=d2-c2r+1xr+1-...-c2nxn ....................... crrxr=dr-crr+1xr+1 -...-crnxn имеющий бесчисленное мн-во реш-й (xr+1,xr+2...xn-свободные переменные).
Примеры линейных пространств. Опр. Мн-во всех действит.чисел или мн-во всех комплекс.чисел будем наз. полем (Р). Не пустое мн-во эл-тов V наз. лин. пр-вом над полем Р, а его эл-ты наз-ся векторами обозн-мые х,у если вып-ся условия: 1.В мн-ве V опр-на алгебр. операция сложения, т.е. для любой пары эл-тов х,у ÎV $ единств.эл-т z ÎV кот.наз-ся суммой векторов у и х, т.е. х + у = z. Спр.оксиомы: а)сложение векторов в мн-веVкоммутативно,т.е. х + у = у + х б)ассоциативно, т.е (х + у)+ z = x +(y + z) в) В мн-ве V $ нулевой эл-т, обозначаемый 0,такой, что для " х из пр-ва V, сумма х + 0 = х г)для " вектора х из V $ противопол-ный ему эл-т –х Î мн-вуV такой, что сумма х +(- х)= 0 2.Определена операция умножения векторов из мн-ва Vна число из поля Р, т.е для" числа a из поля Р и "вектора х из V $ единств. вектор a х ÎР и наз-мый произ-ем х на a, при этом вып-ся оксиомы: д)1× х = х для " х ÎР е)для любых чисел a и b из поля Р и " х их мн-ва Vспр. рав-во: (ab) х =a(b+ х) 3.Операция сложения и умножения связаны дистрибутив. соотношениями: ж)для " х из V и любых a и b из поля Р; (a+b) х =a х +b х з)для " a из Р и" х и у изV спр. рав-во:a(х + у)=a х +a у Опр. ЕслиР- мн-во действ-ых чисел, то лин. пр-во V наз. лин-ным действит. пр-вом. Опр. Если Р- мн-во комплекс. чисел, то Vназ. компл. лин. ПРИМЕР 1. Рассм. мн-во V={0} и рассм.Р- поле действит. чисел. 1. 0+0=0 принадлежит V, т.е. в данном мн-ве опр-на операция сложения. Оксиома: а)0+0=0+0; б)...;в)0; г)0+0=0 2. a× 0=0; a0Î V. Все остальные оксиомы легко проверяются, т.е. мн-во V, состоящее из одного 0, образует действит. лин. пр-во, оно наз. нулевым и обозн. 0- нулевое пр-во ПРИМЕР 2. Рассм. мн-во V={...-2,-1,0,2...} 1. Т.к. сумма целых чисел всегда целое число и принадлежит V, то операция сложения в мн-ве V опр-на, при этом оксиомы а,б,в,г, выполняются. 2.т.к.произ-е целого числа на действ-ное не всегда дает целое число,то операция умнож. на число из поля Рне опр-на, поэтому мн-во всех целых чисел не явл. лин. пр-вом.
Параметрические уравнения прямой на плоскости. Пусть в афинной системе координат (0, X, Y) задана прямая l, ее направляющий вектор
и так как Если обозначить - радиус-векторы соответственно точек M иM0, то параметрическое уравнение прямой. Отсюда следует, что
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.30.203 (0.012 с.) |

 = (m,n) и точка M0 (x 0, y 0) принадлежащая l. Тогда для произвольной точки M (x, у) этой прямой имеем
= (m,n) и точка M0 (x 0, y 0) принадлежащая l. Тогда для произвольной точки M (x, у) этой прямой имеем
 то
то  .
. и
и 

 .
.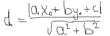 .
.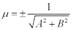 , которое называется нормирующем множителем, то получим
, которое называется нормирующем множителем, то получим (1)
(1) Составим ур. этой плоскости. Пусть М(x,y,z)-произвольная точка этой плоскости. Рассмотр. векторы М1М( x- x1,y-y1,z-z1 ), M1M2( x2-x1,y2-y1,z2-z1 ), M1 M3(x3-x1,y3-y1,z3-z1)
Составим ур. этой плоскости. Пусть М(x,y,z)-произвольная точка этой плоскости. Рассмотр. векторы М1М( x- x1,y-y1,z-z1 ), M1M2( x2-x1,y2-y1,z2-z1 ), M1 M3(x3-x1,y3-y1,z3-z1) Любое полное общее уравнение плоскости преобразуется к виду
Любое полное общее уравнение плоскости преобразуется к виду 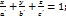 которое наз. уравнением плоскости отрезков. Числа a’,b’,c’ дают отрезки, отсекаемые плоскостью от начала координат на соответствующих осях Ох, Оу, Оz. Используется ур. для быстрого построения плоскости в системе координат.
которое наз. уравнением плоскости отрезков. Числа a’,b’,c’ дают отрезки, отсекаемые плоскостью от начала координат на соответствующих осях Ох, Оу, Оz. Используется ур. для быстрого построения плоскости в системе координат.



 .
. где
где  - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости. Приведение общего уравнения плоскости к нормальному виду:
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости. Приведение общего уравнения плоскости к нормальному виду:  . Здесь
. Здесь  - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если
- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если 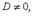 произвольно, если D = 0.
произвольно, если D = 0. Совокупность всех плоскостей проходящих через М0 наз. связкой плоскостей с центром в точке М0.
Совокупность всех плоскостей проходящих через М0 наз. связкой плоскостей с центром в точке М0.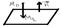 Прямую линию в пространстве рассматривают как пересечение двух различных плоскостей. Координаты точек линии пересечения удовлетворяют ур. каждой пересекающейся плоскости, т.е. координаты точек прямой удовлетворяют системе ур. двух пересекающихся плоскостей. Подчеркнём, что любая линия в пространстве задаётся системой уравнений поверхностей при пересечении которых образуется линия. Если a1x+b1y+c1z+d1=0 – ур. первой плоскости и a2x+b2y+c2z+d2=0 – ур. второй плоскости,
Прямую линию в пространстве рассматривают как пересечение двух различных плоскостей. Координаты точек линии пересечения удовлетворяют ур. каждой пересекающейся плоскости, т.е. координаты точек прямой удовлетворяют системе ур. двух пересекающихся плоскостей. Подчеркнём, что любая линия в пространстве задаётся системой уравнений поверхностей при пересечении которых образуется линия. Если a1x+b1y+c1z+d1=0 – ур. первой плоскости и a2x+b2y+c2z+d2=0 – ур. второй плоскости, , наз. общим уравнением прямой в пространстве.
, наз. общим уравнением прямой в пространстве. Сост. ее ур. Пусть М(x,y,z)-произвольная точка прямой. Рассмотрим вектор М0М= (x-x0,y-y0,z-z0).
Сост. ее ур. Пусть М(x,y,z)-произвольная точка прямой. Рассмотрим вектор М0М= (x-x0,y-y0,z-z0). . Полученное равенство наз. каноническим ур. прямой в пространстве.
. Полученное равенство наз. каноническим ур. прямой в пространстве. , ∆ - определитель основной матрицы, полученной из основной замены итого столбца, столбцов свободных членов.
, ∆ - определитель основной матрицы, полученной из основной замены итого столбца, столбцов свободных членов.


