
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая на плоскости.Формы записиСодержание книги
Поиск на нашем сайте
Прямая на плоскости.Формы записи Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений. Ур-ие прямой с угловым коэф-ом:
K=tgα –угловой коэф-т прямой Общее ур-ие прямой: Ax+Bx+C=0 Ур-ие прямой, прох-ей через данную точку в данном напр-ии y - y0=k(x - x0) Ур-ие прямой, проходящей через две точки
Ур-ие прямой в отрезках
Нормальное ур-ие прямой
17. Эллипсом называется множество всех точек плоскости,сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Эллипс имеет овальную форму.
Теорема:Если r –расстояние от произвольной точки эллипса до какого-нибудь фокуса, d- расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 18. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Каноническое ур-ие гиперболы:
Асимптоты гиперболы:
Асимптоты- прямые, к которым приближается прямая Ур-ие равносторонней гиперболы: x2 - y2=a2 19. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Каноническое ур-ие параболы:
1. Рассмотрим два основных способа задания неупорядоченных множеств: 1. перечисление всех его элементов; 2. описание характеристического (общего) свойства его элементов. 3. алгоритмический 4. задание множ-ва при помощи операций над другими мн-вами Первым способом задаются конечные множества. Примеры: А – множество чисел, являющихся делителями числа 20: А = {1, 2, 4, 5, 10, 20} Вторым способом можно задать конечные множества, бесконечные, пустые. Множество элементов. Обладающих характеристическим свойством Р, обозначается: {x | P(x)} и читается так: множество всех х таких, что х обладает свойством Р(х). {x | x Î R, 2< x < 5 } – бесконечное несчетное множество, а именно, числовой промежуток (2, 5). 2. Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов Операции: Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2} Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). 3. Бином Ньютона (a+b)n=Cn0∙an∙b0+Cn1∙an-1∙b1+Cn2∙an-2∙b2+….+Cnm∙an-m∙bm+ Cnn∙a0∙bn Тут же можно сказать про треугольник Паскаля 4. Тригонометр. Форма компл. числа
Операции над матрицами · Операция сложения матриц вводится только для матриц одинаковых размеров · Суммой двух матриц А и B называется матрица С у которой элементы cij=aij+bij Анологично определяется разность матриц · Произведение матрицы на число называется матрица В у которой элементы bij=k*aij · Матрица–А=(-1)А называется противоположной матрице А.Разность матриц А-Вможно определить как А-В=А+(-В) · Операция умножения двух матриц вводится только тогда когда число столбцов первой матрицы равно числу строк второй матрицы m*n умножить на n*p равно матрицы m*p. · Умножение производиться следующим образом элементы iой строки и kго столбца матрицы произведения матрицы С равен сумме произведений элементов iй строки матрицы А на соответствующие элементы kго столбца матрицы В · Операции сложения и умножения матриц обладают следующими свойствами: 1. А+В=В+А 2. А+(В+С)=(А+В)+С 3. А+0=А 4. А-А=0 5. 1*А=А 6. k*(A+B)=kA+kB 7. (k+c)*A=k*A+c*A 8. k*(c*A)=(k*c)*A Свойства умножения матриц 1. A*(B*C)=(A*B)*C 2. A*(B+C)=A*B+A*C 3. (A+B)*C=A*C+B*C
Вычисление определителей Обратная матрица Обратная матрица существует только для квадратных невырожденных матриц. Невырожденная-если ее определитель отличен от нуля. АВ=ВА-Е,где Е- единичная матрица.
Свойства обратной матрицы:
Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их. СЛАУ. Матрич метод. AX=B X=A-1B (A*. A11, A22 и т.д.) A-1=1/detA * A* Если матрица А системы линейных уравнений невырожденная, т.е. det A ¹ 0, то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы. 20. Уравнения плоскости в пространстве. Уравнение плоскости, проходящей через данную точку Мо (хо, уо, zо) перпендикулярно вектору n=(А, В, С).
Общее ур-е плоскости · Ур-е плоскости, проходящей через три данные точки
Ур-е плоскости в отрезках Нормальное ур-е плоскости
Предел функции в точке. Число A называется пределом функции f (x) при x → x 0 (или в точке x 0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < | x − x 0| < δ, справедливо неравенство | f (x) − A | < ε, т.е. lim x->x0 f(x) = A
Пределы функции слева и справа – односторонние Замечательные пределы. При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел
ББФ. Функция у=f(x) – ббф при x->x0, если для любого числа M>0 существует число δ= δ(M) >0, что для всех х, удовлетворяющих неравенству 0<|x-x0|< δ, выполняется неравенство |f(x)|>M. Записывают lim x->x0 f(x) = 8(бесконечность). БМФ. Функция y= f(x) – бмф при x->x0, если lim x->x0 f(x) = 0. Частное от деления бмф на функцию, имеющую отличный от нуля предел – бмф. Алгебраическая сумма конечного числа бмфункций – бмф. Функция, обратная бмф – ббф и наоборот. Произведение огранич. Фу-ии на бмф – бмф. Произведение двух бмф – бмф. Произведение бмф на число –бмф. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b). Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями. Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна. Понятие производной Рассмотрим функцию y=f(x) на интервале (a;b). Возьмём на этом интервале точку х0 и приращение на оси Ох. Прямая, соединяющая 2 точки (х0;f(x0)) и (x0+Dx;f(x0+Dx))на графике функции называется секущей. Угловой коэффициент секущей равен отношению приращения функции к вызвавшему его приращению аргумента. Производной функции y=f(x) называется предел отношения приращения функции к вызвавшему его приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует) Если предел конечен, то производная конечная, если предел бесконечен, то производная бесконечна.
Правило Лапиталя-Бернули. Правило Лопиталя – Бернулли раскрытия неопределённостей. Теорема. Если f(x) и g(x) – обе бесконечно малые или обе бесконечно большие при
при условии, что предел отношения производных существует. Правило применимо и в случае, когда a=
в произведение
Неопределённости типов ФНп.Частные производные ФНП. Предположим, что задано множество D упорядоченных пар чисел. Если каждой паре из множества D по некоторому правилу сопоставить единственную переменную zÎZ, то говорят, что на множестве D задана функция z=f(x;y). Частные производные первого порядка. Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(х,у) находят по формулам и правилам вычисления производных функции одной переменной (соответственно х или у считается постоянной величиной).
Полный дифференциал Дифференциал функции Если Z=f(M) дифференцируема в точке М (х;у), то её приращение может быть представлено в виде DZ=ADx +BDy+a(Dx;Dy)Dx+b(Dx;Dy)Dy. Определение: (dz) дифференциалом дифференцируемой функции Z в точке М называется линейная относительно в Dx и Dу часть полного приращения функции в точке М, т.е. dZ=ADx+BDy. В правой части DZ=ADx +BDy+a(Dx;Dy)Dx+b(Dx;Dy)Dy третье и четвертое слагаемые являются бесконечно малыми функциями, по этому можно записать приближённое равенство: DZ»dZ, что используется при приближённом вычислении. Дифференциал второго порядка:
Экстремумы Пусть Z=f(M) определена в некоторой окрестности точки M0(x0;y0). Определение: Функция Z=f(x;y), имеет в точке М0 локальный максимум/минимум, если существует такая окрестность точки М0. в которой для каждой точки М из этой окрестности выполняется неравенство: f(M)£f(M0)- максимум / f(M)³f(M0)- минимум. Из определения следует, что если Z имеет экстремум в точке М0, то полное приращение может быть записано: DZ=f(M)-f(M0), DZ£0- для максимума и DZ³0- для минимума. Теорема необходимое условие для локального экстремума: Если Z=f(x;y), имеет экстремум в точке М0, и в этой точке существуют частные производные первого порядка, то они равны нулю. Док-во: зафиксируем одну из переменных у=у0, тогда Z-функция одной переменной(зависит только от х) и она имеет производную в точке х0 и экстремум в точке х0, тогда по необходимому условию экстремума для функции одной переменной: j’(x0)=0 => fx’(x0;y0)=0. Наим. И наиб. Значения функции в замкнутой области. Пусть ф-ия z=f(x;y) определена и непрерывна в замкнутой области D. Тогда она достигает в некоторых токах D своего наибольшего и наименшего значений. Эти значения достигаются функцией в точках, расположенных внутри области D или в точках, лежащих на границе области. Правило нахождения наибольшего и наименшего значений дифференцируемой в интервале: - найти все критические точки функции в интервале и вычислить значения в них - найти наибольшее и наименьшее значения функции на границах интервала - сравнить все найденные значения и выбрать наибольшее и наименьшее
Достаточное условие Теорема достаточное условие локального экстремума: Пусть в точке М0 возможного экстремума и некоторой её окрестности функция Z=f(x;y) имеет частные производные второго порядка. Обозначим: Если D>0, то точка М0 – является точкой локального экстремума, Если D<0. то в точке М0 – экстремума нет, Если D>0, A>0, М0 – точка минимума, Если D>0, A<0, М0 – точка максимума. 49. Неопределённый интеграл Определение: Если функция F(x) – первообразная для f(x) на промежутке (a;b), то множество функций F(x)+C – неопределённый интеграл от f(x). ∫f(x)dx=F(x)+C, где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, dx – переменная интегррования. Первообразная
50. Основные свойства неопределённого интеграла: 1) Производная от неопределенного интеграла = подынтегральной функции. 2) Дифференциал от неопределённого интеграла = подынтегральному выражению. 3) Постоянный множитель м.б. вынесен из под знака интерала. 4) Интеграл от алгебраической суммы/разности функций = алгебраической сумме/разности интегралов. Справедливо для любого конечного количества слогаемых. Формулы Тейлора и Маклорена Формула Тейлора для многочленов.
Если X стремится к Xo, то Rn(X) стремится к 0.
Прямая на плоскости.Формы записи Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений. Ур-ие прямой с угловым коэф-ом:
K=tgα –угловой коэф-т прямой Общее ур-ие прямой: Ax+Bx+C=0 Ур-ие прямой, прох-ей через данную точку в данном напр-ии y - y0=k(x - x0) Ур-ие прямой, проходящей через две точки
Ур-ие прямой в отрезках
Нормальное ур-ие прямой
17. Эллипсом называется множество всех точек плоскости,сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Эллипс имеет овальную форму.
Теорема:Если r –расстояние от произвольной точки эллипса до какого-нибудь фокуса, d- расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 18. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Каноническое ур-ие гиперболы:
Асимптоты гиперболы:
Асимптоты- прямые, к которым приближается прямая Ур-ие равносторонней гиперболы: x2 - y2=a2 19. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Каноническое ур-ие параболы:
1. Рассмотрим два основных способа задания неупорядоченных множеств: 1. перечисление всех его элементов; 2. описание характеристического (общего) свойства его элементов. 3. алгоритмический 4. задание множ-ва при помощи операций над другими мн-вами Первым способом задаются конечные множества. Примеры: А – множество чисел, являющихся делителями числа 20: А = {1, 2, 4, 5, 10, 20} Вторым способом можно задать конечные множества, бесконечные, пустые. Множество элементов. Обладающих характеристическим свойством Р, обозначается: {x | P(x)} и читается так: множество всех х таких, что х обладает свойством Р(х). {x | x Î R, 2< x < 5 } – бесконечное несчетное множество, а именно, числовой промежуток (2, 5). 2. Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов Операции: Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2} Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). 3. Бином Ньютона (a+b)n=Cn0∙an∙b0+Cn1∙an-1∙b1+Cn2∙an-2∙b2+….+Cnm∙an-m∙bm+ Cnn∙a0∙bn Тут же можно сказать про треугольник Паскаля 4. Тригонометр. Форма компл. числа
Операции над матрицами · Операция сложения матриц вводится только для матриц одинаковых размеров · Суммой двух матриц А и B называется матрица С у которой элементы cij=aij+bij Анологично определяется разность матриц · Произведение матрицы на число называется матрица В у которой элементы bij=k*aij · Матрица–А=(-1)А называется противоположной матрице А.Разность матриц А-Вможно определить как А-В=А+(-В) · Операция умножения двух матриц вводится только тогда когда число столбцов первой матрицы равно числу строк второй матрицы m*n умножить на n*p равно матрицы m*p. · Умножение производиться следующим образом элементы iой строки и kго столбца матрицы произведения матрицы С равен сумме произведений элементов iй строки матрицы А на соответствующие элементы kго столбца матрицы В · Операции сложения и умножения матриц обладают следующими свойствами: 1. А+В=В+А 2. А+(В+С)=(А+В)+С 3. А+0=А 4. А-А=0 5. 1*А=А 6. k*(A+B)=kA+kB 7. (k+c)*A=k*A+c*A 8. k*(c*A)=(k*c)*A Свойства умножения матриц 1. A*(B*C)=(A*B)*C 2. A*(B+C)=A*B+A*C 3. (A+B)*C=A*C+B*C
Вычисление определителей
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.008 с.) |





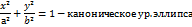



 есть величина постоянная, равная эксцентриситету эллипса:
есть величина постоянная, равная эксцентриситету эллипса: 








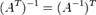

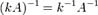 для любого коэффициента.
для любого коэффициента.




 (Первый зам. Предел).
(Первый зам. Предел). или
или  Второй зам. Предел.
Второй зам. Предел. существует и конечен.
существует и конечен.

 т.е. если частное
т.е. если частное 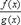 представляется в точке x=a неопределённость типа
представляется в точке x=a неопределённость типа  или
или  , то
, то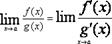
 .Для раскрытия неопределённостей типа
.Для раскрытия неопределённостей типа  будем делать следующие преобразования:
будем делать следующие преобразования:  в частное
в частное 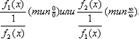 ;
;
 и раскрыть сначала неопределённость
и раскрыть сначала неопределённость 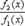 ; если
; если 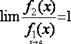 , то приводим выражение к виду:
, то приводим выражение к виду: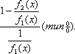
 раскрываются с помощью предварительного логарифмирования и нахождения предела логарифма степени
раскрываются с помощью предварительного логарифмирования и нахождения предела логарифма степени 
 46.Частная производная
46.Частная производная

 Составим матрицу:
Составим матрицу:  , обозначим D=
, обозначим D=  , тогда:
, тогда:
 -
-



 - остаточный член.
- остаточный член. - формула Маклорена.
- формула Маклорена.


