
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальные экстремумы функции одной переменной.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если для любых Х из 0(х нулевое) справедливо неравенство Y max(x0)=y1, ymin(x1)=y2. Необходимое условие экстермума: Если в какой-то точке х0 функция достигает экстремума, то в этой точке производная fштрих (х0)=0 либо не существует точки,при которой производная превращается в 0 не сущ называется критичными точками или точками возмжного экстремума Точка, в которой производная=0 называется стационарной Заметим, что максимум или минимум дифференцируемой функции может находиться лишь в ее критической точке (необходимое условие экстремума). Пусть х0 – критическая (стационарная) точка функции y = f(x) (т.е. внутренняя точка области ее определения, в которой производная равна нулю). Тогда можно сформулировать следующие достаточные условия существования экстремума в этой точке: а) Пусть функция дифференцируема в некоторой окрестности U точки х0, не содержащей других критических точек. Тогда: если при переходе через точку х0 производная f ' меняет свой знак с плюса на минус, х0 – точка (локального) максимума функции; если при переходе через точку х0 производная меняет свой знак с минуса на плюс, х0 – точка (локального) минимума функции; если при переходе через точку х0 производная не меняет свой знак, в точке х0 нет экстремума. б) Пусть в точке х0 существует вторая производная функции f, f ''(x0), не равная нулю. Тогда: если f’’(x0) > 0, х0 – точка (локального) минимума функции; если f’’(x0) < 0, х0 – точка (локального) максимума функции. в) Пусть в точке х0 функция дифференцируема n раз, причем а f(n)(x0) ≠ 0. Тогда: – если n четно и f(n)(x0) < 0, то х0 – точка (локального) максимума функции; – если n четно и f(n)(x0) > 0, то х0 – точка (локального) минимума функции; – если n нечетно, в точке х0 нет экстремума.
Выпуклость функции. Точки перегиба Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Функция f (x) называется выпуклой на интервале (a, b), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x) в любой точке (x0, f (x0)), x0 (a, b). Функция f (x) называется вогнутой на интервале (a, b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f (x) в любой точке (x0, f (x0)), x0 (a, b). Достаточное условие вогнутости (выпуклости) функции. Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда: если f '' (x) > 0 для любого x (a, b), то функция f (x) является вогнутой на интервале (a, b); если f '' (x) < 0 для любого x (a, b), то функция f (x) является выпуклой на интервале (a, b). Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' (x0), то f '' (x0) = 0. 43. Асимптоты графика функций при исследовании графика функции на бесконечность, т.е. при x®+¥ и x®-¥, а так же вблизи точек разрыва часто оказывается, что график сколь угодно близко приближается к той или иной прямой, т.е. асимптоте. Прямая х=х0 – вертикальная асимптота графика функции y=f(x), если хотя бы один из пределов Прямая y=a – горизонтальная асимптота графика y=f(x), при х®±¥, если Прямая y=kx+b называется наклонной асимптотой к графику y=f(x) при х®±¥, если саму функцию y=f(x) можно представить в виде f(x)=kx+b+a(x), где Схема нахождения: вычисляем ФНп.Частные производные ФНП. Предположим, что задано множество D упорядоченных пар чисел. Если каждой паре из множества D по некоторому правилу сопоставить единственную переменную zÎZ, то говорят, что на множестве D задана функция z=f(x;y). Частные производные первого порядка. Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(х,у) находят по формулам и правилам вычисления производных функции одной переменной (соответственно х или у считается постоянной величиной).
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 , то х нулевое называется точкой F(x нулевое)<f(x) локального максимума
, то х нулевое называется точкой F(x нулевое)<f(x) локального максимума или
или  равен ± ¥. Нахождение вертикальных асимптот: 1) точки разрыва и граничные точки на области определения 2) вычисляем односторонний предел при х стремящимся к этим точкам.
равен ± ¥. Нахождение вертикальных асимптот: 1) точки разрыва и граничные точки на области определения 2) вычисляем односторонний предел при х стремящимся к этим точкам. .
.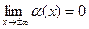 .
. , если этот предел не существует или равен бесконечности, то функция не имеет наклонной асимптоты. Вычисляем
, если этот предел не существует или равен бесконечности, то функция не имеет наклонной асимптоты. Вычисляем  , если его нет или он бесконечен, то асимптоты нет.
, если его нет или он бесконечен, то асимптоты нет.


