
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение дифференциала к приближенным вычислениямСодержание книги
Поиск на нашем сайте Δy можно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dy или Δy»f'(x0)·Δx. Свойства функций, дифференцируемых на отрезке.Теорема Лагранжа Теорема (Лагранжа) Пусть функция Формулу можно записать в виде Свойства функций, дифференцируемых на отрезке.Теорема Коши. Пусть функции
Доказательство. Докажем сначала, что
при некотором Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию
Функция
Значит, функция Вычислим теперь производную функции
Получаем, что
откуда получаем утверждение теоремы:
Замечание.Можно считать функции Отношение
Правило Лапиталя-Бернули. Правило Лопиталя – Бернулли раскрытия неопределённостей. Теорема. Если f(x) и g(x) – обе бесконечно малые или обе бесконечно большие при
при условии, что предел отношения производных существует. Правило применимо и в случае, когда a=
в произведение
Неопределённости типов Возрастание и убывание функции Интервалы возрастания и убывания функции называются интервалами монотонности функции. Иначе говоря, функция [1] Иначе говоря, функция
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

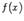 дифференцируема на интервале
дифференцируема на интервале 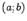 и непрерывна в точках a и b. Тогда найдётся такая точка
и непрерывна в точках a и b. Тогда найдётся такая точка 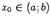 , что
, что 
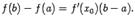 .Если считать, что аргументу a придано приращение
.Если считать, что аргументу a придано приращение 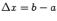 , то функция получает приращение
, то функция получает приращение  . При этих обозначениях формулу мы можем записать в виде
. При этих обозначениях формулу мы можем записать в виде 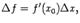 в котором участвуют конечные приращения аргумента и функции. Поэтому формулу называют формулой конечных приращений. Доказательство теоремы Лагранжа. Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика
в котором участвуют конечные приращения аргумента и функции. Поэтому формулу называют формулой конечных приращений. Доказательство теоремы Лагранжа. Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика 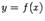 на отрезке
на отрезке  хордой. Конечные приращения
хордой. Конечные приращения 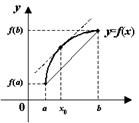
 и
и  дифференцируемы на интервале
дифференцируемы на интервале 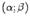 и непрерывны при
и непрерывны при  и
и 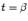 , причём
, причём 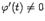 при всех
при всех 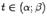 . Тогда в интервале
. Тогда в интервале  найдётся такая точка
найдётся такая точка 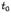 , что
, что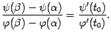
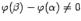 , то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений:
, то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений: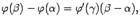
 . Но в правой части этой формулы оба множителя отличны от нуля.
. Но в правой части этой формулы оба множителя отличны от нуля.
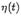 , очевидно, является дифференцируемой при всех
, очевидно, является дифференцируемой при всех 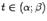 и непрерывной в точках
и непрерывной в точках  и
и  , поскольку этими свойствами обладают функции
, поскольку этими свойствами обладают функции 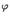 и
и  . Кроме того, очевидно, что при
. Кроме того, очевидно, что при 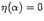 . Покажем, что и
. Покажем, что и 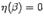 :
: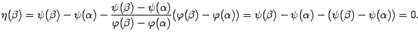
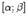 условиям теоремы Ролля. Поэтому существует такая точка
условиям теоремы Ролля. Поэтому существует такая точка 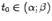 , что
, что  .
.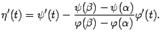
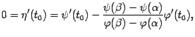
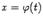 и
и 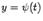 координатами движущейся на плоскости
координатами движущейся на плоскости 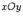 точки, которая описывает линию
точки, которая описывает линию 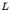 , соединяющую начальную точку
, соединяющую начальную точку  с конечной точкой
с конечной точкой 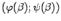 .
.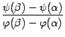 ,как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки
,как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки 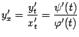 . Значит, дробь
. Значит, дробь 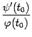 -- это угловой коэффициент касательной к линии
-- это угловой коэффициент касательной к линии 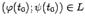 . Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии
. Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии  т.е. если частное
т.е. если частное 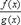 представляется в точке x=a неопределённость типа
представляется в точке x=a неопределённость типа  или
или  , то
, то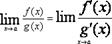
 .Для раскрытия неопределённостей типа
.Для раскрытия неопределённостей типа  будем делать следующие преобразования:
будем делать следующие преобразования:  в частное
в частное 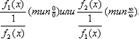 ;
;
 и раскрыть сначала неопределённость
и раскрыть сначала неопределённость 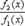 ; если
; если 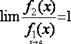 , то приводим выражение к виду:
, то приводим выражение к виду: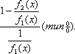
 раскрываются с помощью предварительного логарифмирования и нахождения предела логарифма степени
раскрываются с помощью предварительного логарифмирования и нахождения предела логарифма степени 
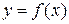 называется возрастающей на интервале
называется возрастающей на интервале 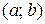 , если большему значению аргумента из этого интервала соответствует большее значение функции.
, если большему значению аргумента из этого интервала соответствует большее значение функции.


