
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных алгебраических уравненийСодержание книги
Поиск на нашем сайте
Матрицы и действия над ними Основные понятия § Матрицей размера
Элементами матрицы aij могут быть, например, действительные или комплексные числа, функции или другие объекты. Условная запись aij обозначает элемент матрицы А, стоящий в i -й строке и j -м столбце. § Если m=n, то матрица называется квадратной порядка n. Элементы aii квадратной матрицы называют элементами главной диагонали. Пример: а 11=1, а 12=0, а 13=-2, а 21=3, а 22=-1, а 23=1. § Матрицы § Матрица А называется нулевой, если все ее элементы § Квадратная матрица А называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны 0. § Диагональная матрица § Квадратная матрица называется треугольной, если равны 0 все элементы под ее главной диагональю (верхнетреугольная матрица) или над главной диагональю (нижнетреугольная матрица):
Действия над матрицами § Суммой двух матриц Легко видеть, что А+В=В+А и А+0=А. § Произведением матрицы Свойства: 1) А + В = В + А (коммутативность сложения матриц) 2) (А+В)+С=А+(В+С)=А+В+С (ассоциативность сложения) 3) А+0=0+А 4) a(А+В)= aА+aВ 5) (a+b)А=aА+bА
§ Произведением матриц А размера
Говорят, что элемент с ij получен в результате умножения i-й строки матрицы А на j-й столбец матрицы В:
причем такое произведение можно составить потому, что строки матрицы А и столбцы матрицы В содержат одинаковое число элементов. Если это не так, то матрицы перемножить нельзя. Отметим, что, вообще говоря, Свойства: 1) 2) А(ВС)=(АВ)С (ассоциативность умножения) 3) a(АВ)=(aА)В=А(aВ) 4) (ab)А=a(bА)=b(aА) 5) (А+В)С=АС+ВС С(А+В)=СА+СВ (дистрибутивность)
Легко видеть, что если Е – единичная матрица порядка n и А – матрица размера
Возведение квадратной матрицы в натуральную степень определяется естественным образом: А 2 =АА и т.д. § Матрица Свойства: 1) 2)
Пример. Даны матрицы:
1) Определить размеры этих матриц; 2) вычислить, если возможно, их попарные произведения; 3) выполнить, если возможно, действия: А+В; 3 АТ+С; ААТ+В 2. Решение: 1) А – матрица размера 2´3; В – квадратная матрица порядка 2 (т.е. размера 2´2), С – матрица размера 3´2. 2) Произведение АВ не существует, т.к. число элементов в строке матрицы А не равно числу элементов в столбце матрицы В. Аналогично, не существует произведение ВС.
3) Найти сумму А+В невозможно, т.к. не совпадают размеры матриц;
Определители Основные понятия § Определитель или детерминант (determinant) квадратной матрицы
где числа А 1j называются алгебраическими дополнениями соответствующих элементов определителя и вычисляются по формулам:
где алгебраические дополнения А 1j вычисляются аналогично предыдущему.
§ Вообще, алгебраическим дополнением Аij для элемента аij называется число Замечание. Вычисление определителя по формулам (1) и (2) называется разложением определителя по первой строке. Любой определитель может быть вычислен с помощью аналогичного разложения по любой строке или столбцу. Понятно, что для разложения определителя выгодно выбирать ту строку (или столбец), в которой содержится наибольшее количество нулевых элементов (конечно, если они есть). Пример: Вычислить определитель Решение: Поскольку определитель содержит нулевой элемент во второй строке, выберем ее для разложения определителя:
2.2. Свойства определителей 1) Определитель не меняется при его транспонировании: Отсюда следует, что любые операции со столбцами определителя эквивалентны аналогичным операциям с его строками.
2) Если в определителе поменять местами две строки (столбца), то определитель изменит знак на противоположный. 3) Если все элементы некоторой строки (столбца) определителя равны нулю, то сам определитель равен нулю. 4) Умножение какой-либо строки (столбца) определителя на произвольное число равносильно умножению определителя на это число. Следовательно, общий множитель элементов фиксированной строки (столбца) можно выносить за знак определителя:
5) Если определитель содержит две одинаковые или пропорциональные строки, то он равен нулю. 6) Если все элементы какой-либо строки (столбца) представлены в виде суммы, то такой определитель можно представить как сумму двух определителей:
7) Определитель не меняется, если к любой строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на фиксированное число:
8) Если А и В – квадратные матрицы одного порядка, то
Пример. Вычислить определитель: Решение: При разложении данного определителя по любой строке нам придется вычислять 4 определителя 3-го порядка, каждый из которых сводится к трем определителям 2-го порядка, при этом придется оперировать достаточно большими числами. Для упрощения вычислений воспользуемся свойствами 6 и 4:
Для вычисления первого определителя используем свойство 5 (ниже запись l 2-2 l 1 означает, что из элементов второй строки определителя мы вычитаем соответствующие элементы первой строки, умноженные на 2 и т.п.) и раскладываем определитель по первому столбцу, в котором оказывается три нулевых элемента:
Поскольку вторая строка полученного определителя равна первой, умноженной на 2, то определитель равен 0. Далее, аналогичным образом применяем свойство 5 для вычисления второго определителя:
Таким образом, искомый определитель D=0.
§ Матрица, определитель которой равен нулю, называется вырожденной, в противном случае – невырожденной.
Обратная матрица Основные понятия § Квадратная матрица А -1 называется обратной к квадратной матрице А того же порядка, если имеет место соотношение
Теорема 3.1. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной. При этом обратная матрица определяется формулой:
где Aij – алгебраические дополнения к элементам аij матрицы АТ.
§ Матрица
Пример. Найти обратную матрицу для матрицы Решение. следовательно, обратная матрица существует. Для ее нахождения запишем матрицу АТ вычислим алгебраические дополнения к ее элементам:
Таким образом, Проверим, является ли найденная матрица действительно обратной для данной матрицы А:
Следовательно, обратная матрица найдена верно.
Решение матричных уравнений Рассмотрим матричное уравнение: АХ=В Пусть А – квадратная невырожденная матрица. Тогда, согласно приведенной выше теореме, существует обратная матрица А -1. Умножим обе части данного уравнения на А -1 слева (напомним, что произведение матриц не является коммутативной операцией!): А -1 АХ=А -1 В Þ ЕХ=А -1 В Þ Х=А -1 В – решение данного матричного уравнения. Аналогично, уравнение ХА=В, где А – квадратная невырожденная матрица, имеет решение Х=ВА -1 (умножаем обе части уравнения на А -1 справа).
Пример. Решить матричное уравнение где Решение:
Проверка:
3.3. Метод элементарных преобразований § Элементарными преобразованиями строк матрицы А называются: - умножение одной строки матрицы на число, отличное от 0; - перемена мест строк; - сложение строк - прибавление к одной строке другой строки, умноженной на число.
1) Для того, чтобы по заданной матрице А найти обратную, следует записать так называемую расширенную матрицу:
и при помощи элементарных преобразований строк привести ее к виду
2) Для того, чтобы решить матричное уравнение АХ=В, сквадратной невырожденной матрицей А, следует записать расширенную матрицу
и при помощи элементарных преобразований строк привести ее к виду
3) Для того, чтобы решить матричное уравнение ХА=В, с квадратной невырожденной матрицей А, следует прежде всего транспонировать это уравнение: АТХТ=ВТ и при помощи элементарных преобразований строк расширенной матрицы Пример: Найти обратную матрицу для матрицы Решение:
Таким образом,
Основные понятия Рассмотрим систему m линейных алгебраических уравнений (СЛАУ) с n неизвестными:
Напомним некоторые определения: § СЛАУ называется однородной, если все свободные коэффициенты равны 0: § Решением СЛАУ называется упорядоченный набор чисел х1,…,хn таких, что при их подстановке в уравнения системы последние обращаются в верные тождества; § СЛАУ называется совместной, если она имеет решение и несовместной в противном случае.
Метод Гаусса решения СЛАУ § Две СЛАУ называются эквивалентными (равносильными), если их решения совпадают. Если в данной СЛАУ поменять местами уравнения, или умножить какое-либо уравнение (обе его части) на число, не равное 0, или заменить одно из уравнений суммой его и какого-либо другого уравнения этой системы, то получится СЛАУ, эквивалентная данной. Такие преобразования являются элементарными преобразованиями системы. Им соответствуют элементарные преобразования строк расширенной матрицы системы § Методом Гаусса называется приведение расширенной матрицы системы при помощи элементарных преобразований строк к упрощенному виду, в котором в левой части расширенной матрицы находится верхнетреугольная матрица. После этого из СЛАУ, соответствующей полученной расширенной матрицы, неизвестные легко находятся последовательным вычислением.
Векторное произведение § 1) 2) 3) векторы Свойства: 1) 2) 3) 4) 5) (геометрический смысл векторного произведения):
Теорема 5.4. Пусть
Доказательство аналогично доказательству соответствующей теоремы о скалярном произведении, с поправкой на свойства векторного произведения. Замечание. Для векторов на плоскости (с двумя координатами) векторное произведение не определено.
Пример. Даны векторы:
Рассмотрим параллелограмм ABCD, построенный на данных векторах. С одной стороны, как известно,
С другой стороны, воспользовавшись геометрическим смыслом векторного произведения, имеем: Найдем векторное произведение:
следовательно, Кроме того, найдем Таким образом,
Смешанное произведение § Смешанным произведением трех векторов Из свойств смешанного произведения особый интерес на практике представляет его геометрический смысл:
Следствие. Три ненулевых вектора компланарны тогда и только тогда, когда их смешанное произведение равно 0. Из определения смешанного произведения и теорем о вычислении скалярного и векторного произведений следует следующая теорема: Теорема 5.6. Пусть
Пример. Выяснить, лежат ли точки A(5; 7; -2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) в одной плоскости. Решение: Данные точки будут лежать в одной плоскости в том и только том случае, если векторы
следовательно, данные точки лежат в одной плоскости.
§6. Аналитическая геометрия на плоскости 6.1. Уравнения прямых на плоскости Рассмотрим плоскость с заданной декартовой системой координат. ü Общее уравнение прямой
Ax+By+C=0 (А2+В2¹0). Это значит, что если точка плоскости принадлежит данной прямой, то ее координаты удовлетворяют уравнению этой прямой и наоборот, если два числа x и y удовлетворяют уравнению прямой, то точка с такими координатами принадлежит соответствующей прямой. В частности, если С=0, А¹0, В¹0, то прямая проходит через начало координат; если А=0, В¹0, С¹0, то прямая параллельна оси Ох; если В=0, А¹0, С¹0, то прямая параллельна оси Оy; ось Ох имеет уравнение y= 0; ось Оy имеет уравнение х= 0.
ü Уравнение прямой с угловым коэффициентом Пусть известно, что точка Р0(х 0, y 0) принадлежит прямой, а угол, образованный данной прямой с положительной полуосью Ох, равен a. Составим уравнение прямой. Пусть точка Р(х, y) – произвольная точка, принадлежащая данной прямой. Тогда рассмотрим прямоугольный треугольник
Коэффициент k называют угловым коэффициентом прямой, а точку Р0 – ее начальной точкой. ü Каноническое уравнение прямой Пусть точка Р0(х 0, y 0) – начальная точка прямой, а вектор
полученное уравнение называется каноническим уравнением прямой на плоскости. ü Если даны две точки Р1(x 1, y 1), P2(x 2, y 2), принадлежащие прямой, то в качестве направляющего вектора мы можем
ü Нормальное уравнение прямой Пусть Р0(х 0, y 0) – начальная точка прямой, а вектор Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы
Полученное уравнение называется нормальным уравнением прямой.
ü Взаимное расположение прямых на плоскости Сравнивая различные виды уравнения прямой на плоскости, легко видеть, что, с точностью до постоянного множителя, А=n 1= v 2, B=n 2=- v 1. Пусть даны две прямые l 1: A 1 x+B 1 y+C 1 =0; l 2: A 2 x+B 2 y+C 2 =0. Тогда: а) l 1ïç l 2 Û б) l 1= l 2 Û в) (в частности, может быть В 1= А 2, В 2= - А 1); г) Точка пересечения прямых определяется системой линейных уравнений:
д) Угол между прямыми равен острому углу между их направляющими векторами, а также острому углу между их нормальными векторами. Следовательно,
Пусть две прямые заданы уравнениями с угловыми коэффициентами: l 1: y=k 1 x+b 1; l 2 y=k 2 x+b 2. Тогда: а) l 1ïç l 2 Û k 1= k 2; б) l 1= l 2 Û k 1= k 2 и b 1= b 2; в) г) Решив совместно данные уравнения, получаем координаты точки пересечения прямых: д) Если
Пример. Дано общее уравнение прямой l: 2 x -5 y +6=0. 1) выяснить, лежит ли на данной прямой точка А(2; 2); 2) написать для прямой l уравнение с угловым коэффициентом; 3) написать уравнение прямой l 1, параллельной данной и проходящей через точку В(1; -3); 4) найти проекцию точки В на прямую l. Решение. 1) Точка А лежит на прямой l Û координаты точки А удовлетворяют уравнению прямой. Проверим: 2×2-5×2+6=0 – верно. Следовательно, точка А принадлежит данной прямой. 2) Для того, чтобы написать уравнение с угловым коэффициентом, выразим из данного общего уравнения у: 3) Из общего уравнения прямой l найдем координаты вектора
4) Сначала решим эту задачу на чертеже. Проведем через точку В прямую l 2, перпендикулярную прямой l и найдем пересечение прямых l и l 2.
Найденная точка N и будет искомой проекцией точки В на прямую l. Теперь проделаем те же действия в аналитической форме. Найдем уравнение прямой l 2. Поскольку
Найдем точку пересечения
Таким образом, искомая точка
Матрицы и действия над ними Основные понятия § Матрицей размера
Элементами матрицы aij могут быть, например, действительные или комплексные числа, функции или другие объекты. Условная запись aij обозначает элемент матрицы А, стоящий в i -й строке и j -м столбце. § Если m=n, то матрица называется квадратной порядка n. Элементы aii квадратной матрицы называют элементами главной диагонали. Пример: а 11=1, а 12=0, а 13=-2, а 21=3, а 22=-1, а 23=1. § Матрицы § Матрица А называется нулевой, если все ее элементы § Квадратная матрица А называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны 0. § Диагональная матрица § Квадратная матрица называется треугольной, если равны 0 все элементы под ее главной диагональю (верхнетреугольная матрица) или над главной диагональю (нижнетреугольная матрица):
Действия над матрицами § Суммой двух матриц Легко видеть, что А+В=В+А и А+0=А. § Произведением матрицы Свойства: 1) А + В = В + А (коммутативность сложения матриц) 2) (А+В)+С=А+(В+С)=А+В+С (ассоциативность сложения) 3) А+0=0+А 4) a(А+В)= aА+aВ 5) (a+b)А=aА+bА
§ Произведением матриц А размера
Говорят, что элемент с ij получен в результате умножения i-й строки матрицы А на j-й столбец матрицы В:
причем такое произведение можно составить потому, что строки матрицы А и столбцы матрицы В содержат одинаковое число элементов. Если это не так, то матрицы перемножить нельзя. Отметим, что, вообще говоря, Свойства: 1) 2) А(ВС)=(АВ)С (ассоциативность умножения) 3) a(АВ)=(aА)В=А(aВ) 4) (ab)А=a(bА)=b(aА) 5) (А+В)С=АС+ВС С(А+В)=СА+СВ (дистрибутивность)
Легко видеть, что если Е – единичная матрица порядка n и А – матрица размера Возведение квадратной матрицы в натуральную степень определяется естественным образом: А 2 =АА и т.д. § Матрица Свойства: 1) 2)
Пример. Даны матрицы:
1) Определить размеры этих матриц; 2) вычислить, если возможно, их попарные произведения; 3) выполнить, если возможно, действия: А+В; 3 АТ+С; ААТ+В 2. Решение: 1) А – матрица размера 2´3; В – квадратная матрица порядка 2 (т.е. размера 2´2), С – матрица размера 3´2. 2) Произведение АВ не существует, т.к. число элементов в строке матрицы А не равно числу элементов в столбце матрицы В. Аналогично, не существует произведение ВС.
3) Найти сумму А+В невозможно, т.к. не совпадают размеры матриц;
Определители Основные понятия § Определитель |
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.173.145 (0.016 с.) |

 называется прямоугольная таблица, состоящая из m строк и n столбцов:
называется прямоугольная таблица, состоящая из m строк и n столбцов: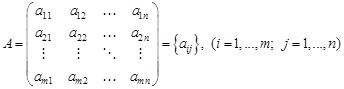
 - матрица размера
- матрица размера  ;
;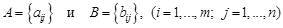 одного размера называются равными, если равны их соответствующие элементы, то есть
одного размера называются равными, если равны их соответствующие элементы, то есть  .
. . Обозначают: А=0.
. Обозначают: А=0. называется единичной, если
называется единичной, если 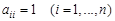 . Единичную матрицу обозначают:
. Единичную матрицу обозначают:  .
.
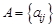 и
и 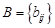
 одного размера называется матрица
одного размера называется матрица 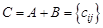 того же размера, где
того же размера, где 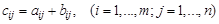
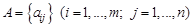 на число l называется матрица
на число l называется матрица 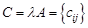 того же размера, где
того же размера, где 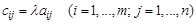 .
.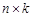 называется матрица С=АВ размера
называется матрица С=АВ размера 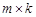 , где
, где .
.
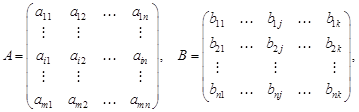
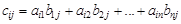 ,
,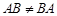 (может даже быть так, что произведение АВ существует, а ВА – нет).
(может даже быть так, что произведение АВ существует, а ВА – нет).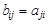 . При этом используют обозначение
. При этом используют обозначение  . Строки матрицы АТ, являются столбцами матрицы А и наоборот.
. Строки матрицы АТ, являются столбцами матрицы А и наоборот.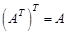
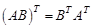
 ,
,  .
.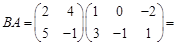

 ;
;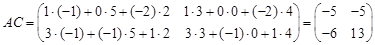 ;
; ;
; 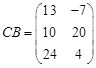 ;
; ;
;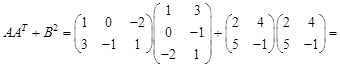
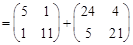
 .
.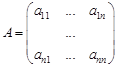 порядка n (или просто определитель n -го порядка) – это числовая характеристика этой матрицы, которую обозначают
порядка n (или просто определитель n -го порядка) – это числовая характеристика этой матрицы, которую обозначают 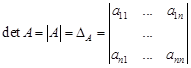 и вычисляют в соответствии со следующим определением:
и вычисляют в соответствии со следующим определением: ;
;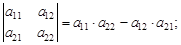
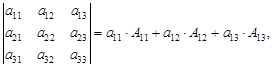 (1)
(1)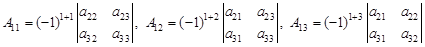
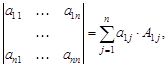 (2)
(2) , где Mij – минор элемента аij, то есть определитель, полученный из
, где Mij – минор элемента аij, то есть определитель, полученный из 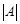 вычеркиванием i -й строки и j -го столбца
вычеркиванием i -й строки и j -го столбца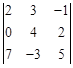

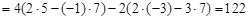 .
.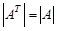 .
.

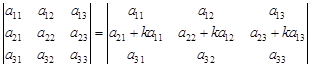


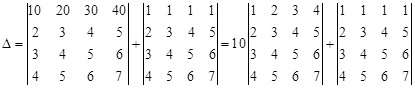
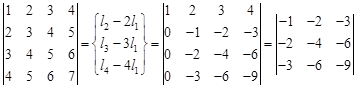
 .
. .
.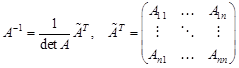 ,
,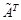 называется присоединенной для матрицы А.
называется присоединенной для матрицы А. .
.
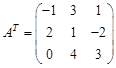
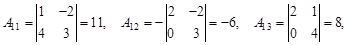
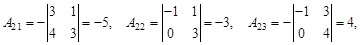
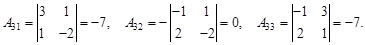
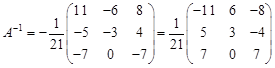 .
.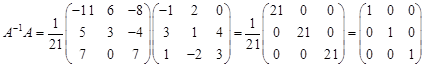
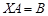 ,
,
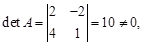
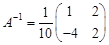
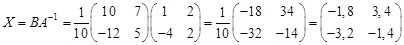 .
.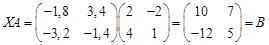 .
.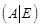
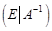 .
.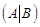
 .
.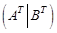 привести ее к виду
привести ее к виду  , после чего транспонировать полученную матрицу ХТ.
, после чего транспонировать полученную матрицу ХТ.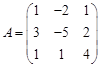 .
.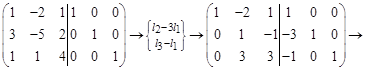
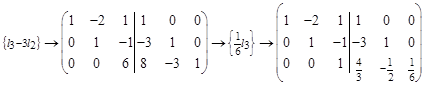

 .
.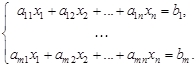 (1)
(1)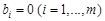 ;
;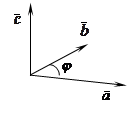 Векторным произведением двух векторов
Векторным произведением двух векторов 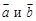 называется вектор
называется вектор 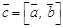 , определяемый следующим образом:
, определяемый следующим образом: , где j - угол между векторами
, где j - угол между векторами 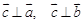
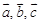 образуют правую тройку векторов.
образуют правую тройку векторов.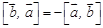 (антикоммутативность);
(антикоммутативность);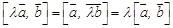 ;
;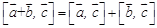
 úï
úï  Þ
Þ 
 модуль векторного произведения равен площади параллелограмма, построенного на векторах
модуль векторного произведения равен площади параллелограмма, построенного на векторах 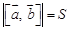
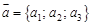 ,
,  . Тогда
. Тогда
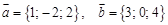 . Найти высоту параллелограмма, построенного на этих векторах, опущенную из конца вектора
. Найти высоту параллелограмма, построенного на этих векторах, опущенную из конца вектора 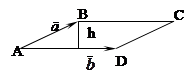 Решение:
Решение: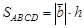 .
.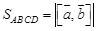 .
. ,
,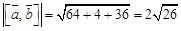 .
.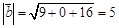
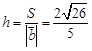 .
.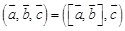 .
. Теорема 5.5. Модуль смешанного произведения трех ненулевых векторов
Теорема 5.5. Модуль смешанного произведения трех ненулевых векторов  .
.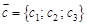 . Тогда
. Тогда 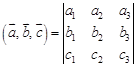 .
.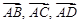 компланарны, что в свою очередь, равносильно утверждению, что смешанное произведение этих векторов равно 0. Проверим, так ли это.
компланарны, что в свою очередь, равносильно утверждению, что смешанное произведение этих векторов равно 0. Проверим, так ли это.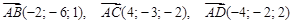 ;
;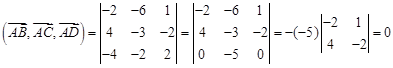 ,
, Утверждение. Любая прямая на плоскости описывается уравнением линии первого порядка:
Утверждение. Любая прямая на плоскости описывается уравнением линии первого порядка: Для того, чтобы написать уравнение прямой, можно использовать различные данные. Соответственно, получаются различные виды уравнения прямой (каждый из которых, тем не менее, можно привести к виду общего уравнения). Собственно, вывод уравнения прямой на плоскости и является доказательством сформулированного выше утверждения.
Для того, чтобы написать уравнение прямой, можно использовать различные данные. Соответственно, получаются различные виды уравнения прямой (каждый из которых, тем не менее, можно привести к виду общего уравнения). Собственно, вывод уравнения прямой на плоскости и является доказательством сформулированного выше утверждения.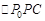 :
:
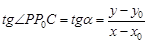 . Обозначив k= tga, получаем уравнение прямой в виде
. Обозначив k= tga, получаем уравнение прямой в виде y-y0=k(x-x0), или y =kx+b (b= y0+kx0)
y-y0=k(x-x0), или y =kx+b (b= y0+kx0) параллелен прямой (он называется ее направляющим вектором).
параллелен прямой (он называется ее направляющим вектором). Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы
Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы 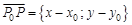 и
и  коллинеарны. Вспомнив свойства координат векторов, запишем это условие в координатной форме:
коллинеарны. Вспомнив свойства координат векторов, запишем это условие в координатной форме:

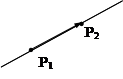 Уравнение прямой, проходящей через две точки:
Уравнение прямой, проходящей через две точки: выбрать вектор
выбрать вектор 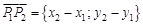 и записать каноническое уравнение:
и записать каноническое уравнение:
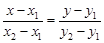
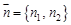 , перпендикулярен данной прямой (тогда его называют нормальным вектором).
, перпендикулярен данной прямой (тогда его называют нормальным вектором).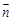 перпендикулярны, следовательно, их скалярное произведение равно нулю:
перпендикулярны, следовательно, их скалярное произведение равно нулю:
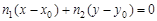 .
. (в частности, может быть А 1= А 2, В 1= В 2);
(в частности, может быть А 1= А 2, В 1= В 2);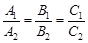 ;
;

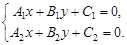
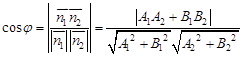
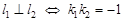 ;
;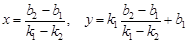 ;
; , то угол между прямыми
, то угол между прямыми 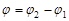 , следовательно:
, следовательно: .
. .
. . Пусть
. Пусть  , тогда
, тогда 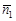 ïê
ïê  . В частности, можно считать, что
. В частности, можно считать, что  . Тогда запишем уравнение прямой l 1 с перпендикулярным вектором, проходящей через точку В: 2(х -1)-5(y +3)=0. Таким образом,
. Тогда запишем уравнение прямой l 1 с перпендикулярным вектором, проходящей через точку В: 2(х -1)-5(y +3)=0. Таким образом, l 1: 2 x -5 y- 17=0.
l 1: 2 x -5 y- 17=0. , то
, то 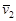 êê
êê 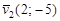 . Запишем уравнение прямой l 2, проходящей через точку В, с направляющим вектором:
. Запишем уравнение прямой l 2, проходящей через точку В, с направляющим вектором: , откуда получаем общее уравнение
, откуда получаем общее уравнение  .
.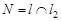 , решив систему уравнений
, решив систему уравнений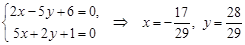
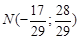 .
.


