
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривые второго порядка на плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§ Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром окружности.
где R – радиус окружности.
§ Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (которая больше, чем расстояние между фокусами).
где а – большая полуось, b – малая полуось эллипса, сумма расстояний от любой точки эллипса до его фокусов равна 2 а, причем a 2= b 2+ c 2. Точки А1(а;0), А2(-а;0), B1(b;0), B2(-b;0) называют вершинами эллипса. Эллипс – центральносимметричная фигура; его центр в рассматриваемом случае совпадает с началом координат. Для того, чтобы изобразить эллипс, описываемый уравнением (1) в системе координат, удобно сначала начертить так называемый осевой прямоугольник, отмеченный на чертеже пунктирной линией, а затем вписать в него эллипс. Отметим, что, если в уравнении вида (1) b > a, то b – большая полуось и эллипс расположен «вертикально», т.е. его фокусы находятся на оси Оу. Величина Взаимное расположение точки М 1(х 1; у 1) и эллипса (1) определяется следующими условиями: если § Если поместить фокусы гиперболы в точках F1(c;0) и F2(-c;0), то эта гипербола будет описываться каноническим уравнением:
где b 2= c 2- a 2; 2 a – постоянная величина из определения гиперболы. Эксцентриситет гиперболы Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А 1(а;0) и А 2(- а;0) называются вершинами гиперболы, отрезок А 1 А 2 называется действительной осью гиперболы, а отрезок В 1 В 2 (где В 1(b;0), B 2(- b;0)) – мнимой осью. Гипербола имеет две асимптоты, уравнения которых Для того, чтобы изобразить гиперболу (2) в системе координат, следует вначале построить осевой прямоугольник (изображен пунктирной линией). Далее, проводят асимптоты гиперболы – прямые, соединяющие противоположные вершины этого прямоугольника. Затем строят симметричные ветви гиперболы, которые проходят через вершины, касаются осевого прямоугольника и приближаются к асимптотам, но не пересекают их.
(3) также является уравнением гиперболы, но действительной ее осью служит отрезок В 1 В 2 оси Оу, так что эта гипербола расположена «вертикально». Гиперболы (2) и (3), у которых одни и те же полуоси и одни и те же асимптоты, но мнимая ось одной гиперболы служит действительной осью для другой, называют сопряженными. § Если директрисой параболы является прямая
Эта парабола расположена симметрично относительно оси Ох. Точка пересечения параболы и ее оси симметрии (в рассматриваемом случае – начало координат) называется вершиной параболы. Уравнение (5) является уравнением «вертикальной» параболы, которая симметрична относительно оси Оу. Если p >0, то ветви параболы обращены в положительную сторону оси (вправо и вверх соответственно), при p <0 – в отрицательную сторону (влево и вниз).
§ Общий вид уравнения кривой второго порядка на плоскости следующий: (6) Ах 2+ Вху + Су 2+ Dx + Ey + F =0. При помощи параллельного переноса и поворота осей координат, любое уравнение вида (6) можно привести к каноническому виду, получив в новой системе координат одно из следующих уравнений (в скобках указаны кривые, задаваемые этими уравнениями):
В частности, если уравнение кривой второго порядка (6) не содержит слагаемого Вху, то оно приводится к каноническому виду путем выделения полных квадратов. Например, уравнение
Пример 1. Составить уравнение окружности, описанной около треугольника, стороны которого заданы уравнениями х - у +1=0, х +5 у +13=0, 2 х + у -1=0. Решение. Найдем координаты вершин треугольника – точек пересечения данных прямых. Для этого решим три системы уравнений:
Получаем точки А (-3;-2), В (0;1), С (2;-3). Будем искать уравнение окружности в общем виде, т.е. (х-а)2+(у-b)2= R 2. Поскольку искомая окружность должна быть описана около треугольника АВС, то координаты этих точек должны удовлетворять уравнению окружности. Подставляя поочередно координаты всех трех точек уравнение окружности, получаем три уравнения относительно неизвестных параметров a, b, R:
Преобразуем систему:
Таким образом, искомое уравнение имеет вид
Пример 2. Привести уравнение к каноническому виду, определить тип задаваемой им кривой, построить: 16 х 2+25 у 2-32 х +50 у -359=0. Решение. Выделим в левой части данного уравнения полные квадраты: 16 х 2-32 х =16(х 2-2 х)=16(х 2-2 х +1-1)=16(х -1)2-16, 25 у 2+50 у =25(у +1)2-25. Перенеся свободный коэффициент в правую часть уравнения, получаем: 16(х-1)2+25(у+1)2=400.
Получили уравнение эллипса с центром в точке (1;-1) и полуосями а =5, b =4. Построим его:
§7. Аналитическая геометрия в пространстве 7.1. Уравнение плоскости в пространстве Рассмотрим трехмерное пространство с заданной декартовой системой координат. ü Общее уравнение плоскости
ü Нормальное уравнение плоскости Пусть известна точка М 0(х 0; у 0; z 0), принадлежащая плоскости (начальная точка) и ненулевой вектор Произвольная точка пространства М (х; у; z) принадлежит данной плоскости тогда и только тогда, когда
Если в этом уравнении раскрыть скобки, получится общее уравнение плоскости: Ах+Ву+Cz+D =0 (где D=-Ax 0 -By 0 -Cz 0). Этот факт и доказывает сформулированное выше утверждение. ü Уравнение плоскости по трем точкам Пусть даны три точки, принадлежащие плоскости: М 1(х 1; у 1; z 1), M 2(x 2; y 2; z 2), M 3(x 3; y 3; z 3).
раскрыв определитель по первой строке, получаем общее уравнение плоскости. Аналогично, если дана точка М 0(х 0; у 0; z 0), принадлежащая плоскости (начальная точка) и два вектора
7.2. Уравнения прямой в пространстве ü Пусть прямая задана как пересечение двух плоскостей:
Тогда система ü Пусть задана начальная точка прямой Р 0(х 0, y 0, z 0)Î l и направляющий вектор
Аналогичным образом составляются канонические уравнения прямой, проходящей через две данные точки Р1 и Р2, так что в качестве направляющего вектора можно выбрать вектор ü Параметрические уравнения прямой
Эти уравнения означают, что для каждой точки прямой существует значение параметра t через который выражаются координаты этой точки и наоборот, для каждого значения t точка с соответствующими координатами принадлежит прямой. Применение этих уравнений удобно, например, для нахождения точки пересечения прямой и плоскости.
7.3. Взаимное расположение прямых и плоскостей Пусть прямые и плоскости заданы своими уравнениями:
Заметим, что эти уравнения позволяют нам выписать нормальные векторы данных плоскостей: Тогда: а) б) в) углом между плоскостями называется острый угол между их нормальными векторами: г) (в частности, может быть д)
(в частности, может быть ж)
и) угол между прямой l 1 и плоскостью p 1 равен углу между прямой и ее проекцией на плоскость, но удобнее его находить при помощи угла между прямой и перпендикуляром к плоскости:
Пример. Найти точку Q, симметричную точке P (10; -5; 6) относительно плоскости a, в которой лежат прямые
Решение: Прежде всего, найдем уравнение плоскости a. Эта плоскость проходит через точку М1(-1; 3; 2) параллельно двум векторам
Раскрыв определитель по первой строке, получаем:
далее, сократим на 4 и раскроем скобки:
Для того, чтобы найти точку, симметричную данной относительно плоскости, необходимо опустить из точки Р на плоскость a перпендикуляр l, затем найти точку N пересечения полученной прямой и плоскости и отложить на этой прямой отрезок NQ, равный от резку PN. Поскольку
Чтобы найти точку пересечения прямой и плоскости
Таким образом, координаты точки N:
Далее, точка N является серединой отрезка PQ, следовательно, аналогично Таким образом, Q (-14; 7; -2).
7.4. Поверхности второго порядка В общем виде поверхность второго порядка в трехмерном пространстве задается алгебраическим уравнением второго порядка:
Как и в случае кривых второго порядка на плоскости, при помощи параллельного переноса и поворота осей системы координат такое уравнение сводится к одному из канонических уравнений, а поверхность принадлежит к одному из типов, описанных ниже (либо вырождается в точку, две прямые, две плоскости или мнимую поверхность). ü
На примере эллипсоида опишем процесс построения поверхности. Для этого применяется метод линий уровня, то есть линий пересечения поверхности с плоскостями, параллельными, например, плоскости хОу. При z =0 (т.е. в плоскости хОу) получаем При z =const, При При z =const, Итак, линии уровня данной поверхности – эллипсы. Для того, чтобы окончательно выяснить, как выглядит поверхность, найдем пересечения с плоскостями xOz и yOz. При y =0 получаем При х =0 получаем
 
ü Гиперболический параболоид
ü Эллиптический цилиндр Цилиндрические поверхности – поверхности, образованные прямыми, параллельными некоторой оси. Уравнение такой поверхности не содержит переменной, соответствующей этой оси. Для того, чтобы построить цилиндрическую поверхность, надо построить образующую, которую задает данное уравнение в одной из координатных плоскостей и восстановить над ней цилиндр.
образующая этой поверхности – эллипс в плоскости xOy и прямые, параллельные оси Oz.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.180 (0.01 с.) |

 Если выбрать систему координат на плоскости так, чтобы начало координат совпадало с центром окружности, то ее уравнение будет выглядеть так:
Если выбрать систему координат на плоскости так, чтобы начало координат совпадало с центром окружности, то ее уравнение будет выглядеть так:
 ,
, Если система координат расположена по отношению к эллипсу так, чтобы фокусы эллипса находились на оси Ох на равных расстояниях от начала координат в точках F1(c;0) и F2(-c;0), то этот эллипс будет описываться каноническим уравнением:
Если система координат расположена по отношению к эллипсу так, чтобы фокусы эллипса находились на оси Ох на равных расстояниях от начала координат в точках F1(c;0) и F2(-c;0), то этот эллипс будет описываться каноническим уравнением: (1)
(1) 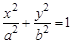 , (a > b)
, (a > b) называется эксцентриситетом эллипса и характеризует его «сплюснутость». Если e = 0, то с = 0, a = b, в этом случае эллипс превращается в окружность. Если e =1, то с=а, следовательно, b =0, и эллипс вырождается в отрезок F1F2.
называется эксцентриситетом эллипса и характеризует его «сплюснутость». Если e = 0, то с = 0, a = b, в этом случае эллипс превращается в окружность. Если e =1, то с=а, следовательно, b =0, и эллипс вырождается в отрезок F1F2. , то точка лежит на эллипсе; если
, то точка лежит на эллипсе; если  , то точка лежит внутри эллипса; если
, то точка лежит внутри эллипса; если  , то точка лежит вне эллипса.
, то точка лежит вне эллипса. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (которая меньше, чем расстояние между фокусами).
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (которая меньше, чем расстояние между фокусами). (2)
(2)  ,
, .
.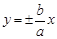 . Как и эллипс, гипербола – центральносимметричная фигура; ее центр в данном случае совпадает с началом координат.
. Как и эллипс, гипербола – центральносимметричная фигура; ее центр в данном случае совпадает с началом координат.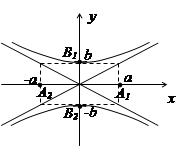 Уравнение
Уравнение
 Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. , а фокусом – точка F(p/2;0), то уравнение параболы имеет вид
, а фокусом – точка F(p/2;0), то уравнение параболы имеет вид (4)
(4)  .
. .
. (вырожденный эллипс - единственная точка (0;0))
(вырожденный эллипс - единственная точка (0;0)) (мнимый эллипс, которому не принадлежит ни одна точка плоскости)
(мнимый эллипс, которому не принадлежит ни одна точка плоскости) (две прямые:
(две прямые:  или
или  ,
, 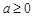 (две прямые:
(две прямые:  или
или  )
) или
или  , a >0 (мнимые прямые, которым не принадлежит ни одна точка плоскости)
, a >0 (мнимые прямые, которым не принадлежит ни одна точка плоскости) описывает эллипс, центр которого смещен из начала координат в точку (х 0; у 0).
описывает эллипс, центр которого смещен из начала координат в точку (х 0; у 0).



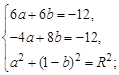 откуда
откуда  .
. .
. Для того, чтобы привести это уравнение к каноническому виду, разделим обе части уравнения на 400:
Для того, чтобы привести это уравнение к каноническому виду, разделим обе части уравнения на 400:
 Утверждение. Любая плоскость в трехмерном пространстве описывается уравнением первого порядка: Ах+Ву+Cz+D =0 (A 2+ B 2+ C 2¹0)
Утверждение. Любая плоскость в трехмерном пространстве описывается уравнением первого порядка: Ах+Ву+Cz+D =0 (A 2+ B 2+ C 2¹0)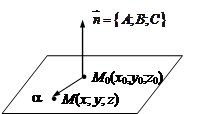 В частности, если D =0, то плоскость проходит через начало координат; плоскость хОу имеет уравнение z =0; плоскость xOz имеет уравнение y =0; плоскость yOz имеет уравнение х =0.
В частности, если D =0, то плоскость проходит через начало координат; плоскость хОу имеет уравнение z =0; плоскость xOz имеет уравнение y =0; плоскость yOz имеет уравнение х =0.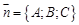 , перпендикулярный этой плоскости (его называют нормальным вектором плоскости).
, перпендикулярный этой плоскости (его называют нормальным вектором плоскости). , то есть
, то есть  . Записывая скалярное произведение в координатной форме, получаем нормальное уравнение плоскости:
. Записывая скалярное произведение в координатной форме, получаем нормальное уравнение плоскости:


 Произвольная точка пространства М (х; у; z) принадлежит данной плоскости тогда и только тогда, когда векторы
Произвольная точка пространства М (х; у; z) принадлежит данной плоскости тогда и только тогда, когда векторы 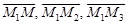 компланарны, то есть их смешанное произведение равно нулю. Таким образом, получаем уравнение данной плоскости в виде:
компланарны, то есть их смешанное произведение равно нулю. Таким образом, получаем уравнение данной плоскости в виде: ;
;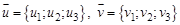 , параллельные этой плоскости, то уравнение плоскости записывают в виде
, параллельные этой плоскости, то уравнение плоскости записывают в виде

 Общее уравнение прямой
Общее уравнение прямой , где
, где ,
, .
. задает множество точек прямой и называется общим уравнением прямой.
задает множество точек прямой и называется общим уравнением прямой. Канонические уравнения прямой
Канонические уравнения прямой .
. Тогда
Тогда  , откуда получаем уравнения прямой в виде
, откуда получаем уравнения прямой в виде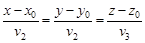 .
. .
. Введение коэффициента пропорциональности t в канонические уравнения прямой позволяет записать ее параметрические уравнения:
Введение коэффициента пропорциональности t в канонические уравнения прямой позволяет записать ее параметрические уравнения:
 ,
, 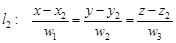 .
. , направляющие векторы прямых:
, направляющие векторы прямых:  и начальные точки прямых:
и начальные точки прямых:  .
. ;
; ;
;

 );
); ;
;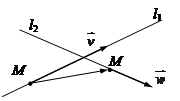 е)
е) 
 );
); компланарны
компланарны ;
;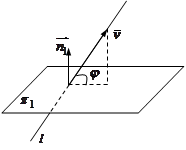 з) углом между прямыми называется острый угол между их направляющими векторами:
з) углом между прямыми называется острый угол между их направляющими векторами:  ;
; .
.
 и
и  , следовательно, ее уравнение имеет вид:
, следовательно, ее уравнение имеет вид: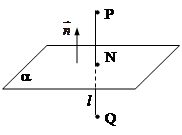
 .
. ,
, .
. , то в качестве направляющего вектора прямой мы можем выбрать нормальный вектор плоскости, координаты которого находятся из уравнения плоскости:
, то в качестве направляющего вектора прямой мы можем выбрать нормальный вектор плоскости, координаты которого находятся из уравнения плоскости:  . Следовательно, уравнение перпендикуляра:
. Следовательно, уравнение перпендикуляра: .
. , запишем уравнения прямой l в параметрической форме и подставим в уравнение плоскости a:
, запишем уравнения прямой l в параметрической форме и подставим в уравнение плоскости a: ;
;
 .
. .
. ,
, .
. .
. Эллипсоид
Эллипсоид
 - эллипс с полуосями a, b.
- эллипс с полуосями a, b. (в плоскостях, параллельных хОу) получаем
(в плоскостях, параллельных хОу) получаем  - эллипсы с полуосями, меньшими чем a, b.
- эллипсы с полуосями, меньшими чем a, b. получаем
получаем 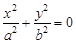 - точка (0; 0).
- точка (0; 0). получаем мнимые эллипсы, то есть пересечений с поверхностью нет.
получаем мнимые эллипсы, то есть пересечений с поверхностью нет. - эллипс с полуосями а, с.
- эллипс с полуосями а, с. - эллипс с полуосями b, c.
- эллипс с полуосями b, c.


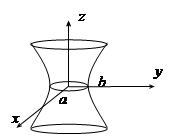


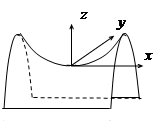

 Эллиптический цилиндр задается уравнением
Эллиптический цилиндр задается уравнением






