
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линии второго порядка на плоскости(окружность и эллипс-смотри 24 билет)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Окружность. Простейшей кривой второго порядка является окружность. Окружность - это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности.
В частности, полагая 2). Эллипсом (круг на координатных осях) называется геометрическое место точек на плоскости, сумма расстояний от каждой из которых до двух фиксированных точек F1 и F2(фокусов) есть величина постоянная. Каноническое уравнение x2/a2+y2/b2=1, уравнение касательной в точке M(x0; y0) y-y0=b2*x0/a2*y0 * (x-x0), фокусы эллипса F1(-c;0), F2(c;0) c=a2-b2 (под корнем это!), эксцентрисетет e=c/a, директрисы x=d=a/e, x=-d=-a/e, r1/d1=r2/d2=e, оптическое свойство F1MA=F2MB, отношение полуосей b/a=1-e2(вот это выражение под корнем), расстояние от точки эллипса до фокусов(фокальные радиусы) r1=MF1=a+ex; r2=MF2=a-ex; r1+r2=2a, параметрическое уравнение x=accost, y=bsint (интервал от о до 2Пи принадледит t) 3). Гиперболой называется геометрическое место точек на плоскости, разность расстояний от каждой из которых до двух данных точек F1 и F2. Каноническое уравнение x2/a2-y2/b2=1 и сопряжение с отрицательной еденичкой, уравнение касательной в точке M(x0, y0) y-y0=b2* x0/a2*y0 * (x-x0),асимптоты y= плюс минус b/a *x, эксцентрисетет e=c/a, директрисы x=d=a/e, x=-d=-a/e, r1/d1=r2/d2=e, оптическое свойство F1MA=AMF2, расстояние от точки геперболы до фокусов(фокальные радиусы) r1=MF1(под модулем)=a+ex(модуль); r2=MF2(модуль)=a-ex(модуль); r1+r2 (модуль)=2a. 25. Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов Билет 26. Цилиндрические поверхности. Поверхности вращения и их канонические уравнения. 27. Поверхности второго порядка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени: a 11 x 2 +2 a 12 xy + a 22 y 2 + 2 a 10 x a 33 z 2 + 2 a 20 y + a 00 = 0 (*) a 112 + a 122 + a 222 =(не равно) 0 Существует 9 кривых второго порядка: 1). Существующая прямая пересекает кривую второго порядка не более чем в 2-х точках. 2). Три основных кривых второго порядка: эллипс, гипербола и парабола. Виды:1) эллипсоиды(эллипсоиды, мнимые эллипсоиды);2) гиперболоиды: (однополостные гиперболоиды, двуполостные гиперболоиды); 3) параболоиды (эллиптические параболоиды, гиперболические параболоиды); 4) конусы второго порядка:(конусы, мнимые конусы); 5) цилиндры второго порядка(эллиптические цилиндры, мнимые эллиптические цилиндры, гиперболические цилиндры, параболические цилиндры).
Билет 28. Линейное, или векторное пространство Простейшие свойства 1). Векторное пространство является абелевой группой по сложению.2). Нейтральный элемент Билет 29. Подпространство Линейное подпространство или векторное подпространство ― непустое подмножество Свойства подпространств 1). Пересечение любого семейства подпространств — снова подпространство;2). Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 945; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат 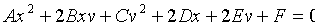 0(нулю) (11.1) Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Виды это окружность и эллипс.
0(нулю) (11.1) Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Виды это окружность и эллипс.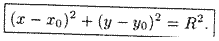 (11.2)это каноническим уравнением окружности
(11.2)это каноническим уравнением окружности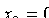 и
и  , получим уравнение окружности с центром в начале координат
, получим уравнение окружности с центром в начале координат 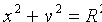 . Уравнение окружности (11.2) после несложных преобразований примет вид
. Уравнение окружности (11.2) после несложных преобразований примет вид  . При сравнении этого уравнения с общим уравнением кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия: 1) коэффициенты при x2 и у2 равны между собой; 2) отсутствует член, содержащий произведение xу текущих координат. Билет 24.1). Парабола- это геометрическое место точекна плоскости, одинаково удаленных от данной точки(фокуса) и данной прямой(директрисы).Каноническое уравнение y2=2px, фокус F(P/2;0); директриса x=- P/2, r= MF(модуль)=x+P/2(модуль)
. При сравнении этого уравнения с общим уравнением кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия: 1) коэффициенты при x2 и у2 равны между собой; 2) отсутствует член, содержащий произведение xу текущих координат. Билет 24.1). Парабола- это геометрическое место точекна плоскости, одинаково удаленных от данной точки(фокуса) и данной прямой(директрисы).Каноническое уравнение y2=2px, фокус F(P/2;0); директриса x=- P/2, r= MF(модуль)=x+P/2(модуль)
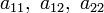 отличен от нуля. Классификация кривых второго порядка: 1). Невырожденные кривые Кривая второго порядка называется невырожденной, если
отличен от нуля. Классификация кривых второго порядка: 1). Невырожденные кривые Кривая второго порядка называется невырожденной, если  (треугольничек – это определитель) Могут возникать следующие варианты:1). Невырожденная кривая второго порядка называется центральной, если
(треугольничек – это определитель) Могут возникать следующие варианты:1). Невырожденная кривая второго порядка называется центральной, если  2). эллипс — при условии
2). эллипс — при условии  и
и 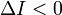 ; 3). частный случай эллипса — окружность — при условии
; 3). частный случай эллипса — окружность — при условии  или
или  40. мнимый эллипс (ни одной вещественной точки) — при условии
40. мнимый эллипс (ни одной вещественной точки) — при условии 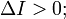 5). гипербола — при условии
5). гипербола — при условии  5). Невырожденная кривая второго порядка называется нецентральной, если
5). Невырожденная кривая второго порядка называется нецентральной, если 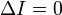 6). парабола — при условии
6). парабола — при условии 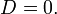 Вырожденные кривые Кривая второго порядка называется вырожденной, если
Вырожденные кривые Кривая второго порядка называется вырожденной, если  . Могут возникать следующие варианты: 1). вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии
. Могут возникать следующие варианты: 1). вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии 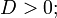 2). пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии
2). пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии  4). пара вещественных параллельных прямых — при условии
4). пара вещественных параллельных прямых — при условии 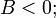 5). одна вещественная прямая (две слившиеся параллельные прямые) — при условии
5). одна вещественная прямая (две слившиеся параллельные прямые) — при условии  6). пара мнимых параллельных прямых (ни одной вещественной точки) — при условии
6). пара мнимых параллельных прямых (ни одной вещественной точки) — при условии 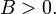 Виды кривых второго порядка: парабола, эллипс и гипербола(рассказать о них все!!билет24)
Виды кривых второго порядка: парабола, эллипс и гипербола(рассказать о них все!!билет24)


 над полем
над полем  — это непустое множество
— это непустое множество 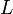 , на котором введены операции:1).сложения, то есть каждой паре элементов множества
, на котором введены операции:1).сложения, то есть каждой паре элементов множества 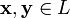 ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 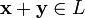 и.2). умножения на скаляр (то есть элемент поля
и.2). умножения на скаляр (то есть элемент поля  и любому элементу
и любому элементу 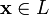 ставится в соответствие единственный элемент из
ставится в соответствие единственный элемент из  . При этом на операции накладываются следующие условия:1).
. При этом на операции накладываются следующие условия:1).  , для любых
, для любых  , для любых
, для любых  (ассоциативность сложения)3). существует такой элемент
(ассоциативность сложения)3). существует такой элемент  , что
, что  для любого
для любого 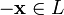 , что
, что 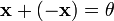 (существование противоположного элемента относительно сложения).5).
(существование противоположного элемента относительно сложения).5).  (ассоциативность умножения на скаляр);6).
(ассоциативность умножения на скаляр);6).  (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).7).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).7).  (дистрибутивность умножения на вектор относительно сложения скаляров); Элементы множества
(дистрибутивность умножения на вектор относительно сложения скаляров); Элементы множества 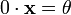 для любого
для любого  для любого
для любого  для любых
для любых  и
и  для любого
для любого  линейного пространства
линейного пространства 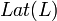 . Чтобы подмножество было подпространством, необходимо и достаточно, чтобы1).
. Чтобы подмножество было подпространством, необходимо и достаточно, чтобы1).  ; 2). для всякого вектора
; 2). для всякого вектора  , вектор
, вектор  также принадлежал
также принадлежал 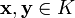 , вектор
, вектор  также принадлежал
также принадлежал  , является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.
, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными. определяется как множество, содержащее всевозможные суммы элементов
определяется как множество, содержащее всевозможные суммы элементов  :
: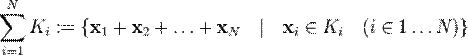 .
.


