Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Билет 30. Линейная комбинация, оболочка, линейная зависимость и независимость векторов
Линейная комбинация векторов. Пусть дана совокупность двух векторов и совокупность чисел. Тогда сумма произведения лямбда1*вектор а1+лямбда2*вектор а2+…+лямбда n*вектор An называется линейной комбинацией векторов. Линейная зависимость и независимость векторов 1). Совокупность векторов а1,а2,…,Аn называют линейно независимой если их линейная комбинация может быть равно 0 только в том случае, когда все числа лямбды равны 0. 2). Совокупность векторов а1,а2,…,Аn называют линейно зависимой если их линейная комбинация может быть равно 0 только в том случае, когда не все числа лямбды равны 0.
Критерий линейной зависимости векторов
Для того чтобы векторы  (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных. (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
Линейная оболочка  подмножества подмножества  линейного пространства линейного пространства 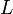 — пересечение всех подпространств — пересечение всех подпространств 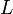 , содержащих , содержащих  . .
Линейная оболочка является подпространством 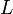 . Линейная оболочка также называется подпространством, порожденным . Линейная оболочка также называется подпространством, порожденным  . Говорят также, что линейная оболочка . Говорят также, что линейная оболочка  натянута на множество натянута на множество  . Линейная оболочка . Линейная оболочка  состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из  . В частности, если . В частности, если  — конечное множество, то — конечное множество, то  состоит из всех линейных комбинаций элементов состоит из всех линейных комбинаций элементов  . Если . Если  — линейно независимое множество, то оно является базисом — линейно независимое множество, то оно является базисом  и тем самым определяет его размерность. и тем самым определяет его размерность.
Билет 32. Фундаментальная система решений системы линейных однородных уравнений
Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с n неизвестными переменными называют совокупность (n – r) линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы.
Если обозначить линейно независимые решения однородной СЛАУ как X(1), X(2), …, X(n-r) (X(1), X(2), …, X(n-r) – это матрицы столбцы размерности n на 1), то общее решение этой однородной системы  представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С1, С2, …, С(n-r), то есть, представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С1, С2, …, С(n-r), то есть,  .ОРОСЛАУ- это общее решение однородной системы линейных алгебраических уравнений (орослау) .ОРОСЛАУ- это общее решение однородной системы линейных алгебраических уравнений (орослау)
Процесс построения фундаментальной системы решений однородной СЛАУ:
Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1, 0, 0, …, 0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, (например методом Крамера). Так будет получено X(1) - первое решение фундаментальной системы. Если придать свободным неизвестным значения 0, 1, 0, 0, …, 0 и вычислить при этом основные неизвестные, то получим X(2). И так далее. Если свободным неизвестным переменным придадим значения 0, 0, …, 0, 1 и вычислим основные неизвестные, то получим X(n-r). Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде  . .
Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде  , где , где  общее решение соответствующей однородной системы, а общее решение соответствующей однородной системы, а  - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0, 0, …, 0 и вычислив значения основных неизвестных. - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0, 0, …, 0 и вычислив значения основных неизвестных.
Разберем на примерах. (последний лист!!!если попадется)
Билет 33. Определение линейного оператора и его матрицы. Ядро и образ линейного оператора Пусть заданы линейные пространства  и и  . Правило, по которому каждому элементу . Правило, по которому каждому элементу  ставится в соответствие единственный элемент ставится в соответствие единственный элемент 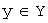 , называется ОПЕРАТОРОМ, действующим в линейных пространствах , называется ОПЕРАТОРОМ, действующим в линейных пространствах  . Результат действия оператора . Результат действия оператора  на элемент на элемент  обозначают обозначают  или или  . Если элементы . Если элементы  и и  связаны соотношением связаны соотношением  , то , то  называют образом элемента называют образом элемента  ; элемент ; элемент  прообразом элемента прообразом элемента  . Множество элементов линейного пространства . Множество элементов линейного пространства  , для которых определено действие оператора , для которых определено действие оператора  , называют областью определения оператора и обозначают , называют областью определения оператора и обозначают  . Множество элементов линейного пространства . Множество элементов линейного пространства  , которые являются образами элементов из области определения оператора , которые являются образами элементов из области определения оператора  , называют образом оператора и обозначают , называют образом оператора и обозначают  . Если . Если  , то , то 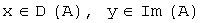 . Оператор . Оператор  , действующий в линейных пространствах , действующий в линейных пространствах  называется линейным оператором, если называется линейным оператором, если  и и 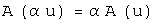 для любых для любых  и для любого числа и для любого числа  . Если пространства . Если пространства  и и  совпадают, то говорят, что оператор действует в пространстве совпадают, то говорят, что оператор действует в пространстве  . В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве . В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве  . Образ и ядро линейного оператора Рассмотрим линейный оператор . Образ и ядро линейного оператора Рассмотрим линейный оператор  , действующий в конечномерном линейном пространстве , действующий в конечномерном линейном пространстве  . Доказано, что образ . Доказано, что образ  линейного оператора линейного оператора  линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается 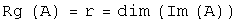 . Ядром линейного оператора называется множество элементов из . Ядром линейного оператора называется множество элементов из  , образом которых является нулевой элемент. Ядро оператора обозначают , образом которых является нулевой элемент. Ядро оператора обозначают 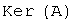 : : 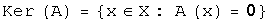 . А также:1). ранг оператора равен рангу его матрицы; 2). ядро оператора совпадает с множеством решений линейной однородной системы с 3). столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем. . А также:1). ранг оператора равен рангу его матрицы; 2). ядро оператора совпадает с множеством решений линейной однородной системы с 3). столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
Билет 34. Преобразование матрицы линейного оператора при изменении базиса Рассмотрим линейный оператор  , действующий в конечномерном линейном пространстве , действующий в конечномерном линейном пространстве  , ,  и пусть и пусть 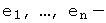 базис в базис в  . Обозначим через . Обозначим через  образы базисных векторов образы базисных векторов  . Матрица . Матрица
 столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейномпространстве, отвечает единственная квадратная матрица порядка n; и обратно столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейномпространстве, отвечает единственная квадратная матрица порядка n; и обратно  каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения
 с одной стороны, связывают координаты образа с одной стороны, связывают координаты образа  с координатами прообраза с координатами прообраза  , с другой стороны, описывают действие оператора, заданного матрицей , с другой стороны, описывают действие оператора, заданного матрицей  . При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве . При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве  произошел переход от базиса произошел переход от базиса  к базису к базису  . Связь между матрицей . Связь между матрицей  оператора оператора  в базисе в базисе  и матрицей и матрицей  этого оператора в базисе этого оператора в базисе  задается формулой. задается формулой.
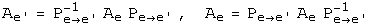
Здесь   матрица перехода от базиса матрица перехода от базиса  к базису к базису  и обратная к ней. и обратная к ней.
Билет 35. Собственные векторы и собственные значения линейного оператора
Ненулевой вектор 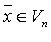 называется собственным вектором линейного оператора называется собственным вектором линейного оператора  , если , если  ( ( для комплексного для комплексного  ), такое, что ), такое, что  Число Число  называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору. Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору. Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор 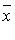 имеет координатный столбец X, то имеет координатный столбец X, то 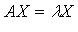 или или  Собственные числа Собственные числа  линейного оператора линейного оператора  - корни характеристического уравнения - корни характеристического уравнения  , где , где  - матрица оператора f, - матрица оператора f,  - символ Кронекера. Для каждого собственного значения - символ Кронекера. Для каждого собственного значения 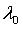 соответствующие собственные векторы могут быть найдены из матричного уравнения соответствующие собственные векторы могут быть найдены из матричного уравнения  или соответствующей ему системы линейных уравнений или соответствующей ему системы линейных уравнений
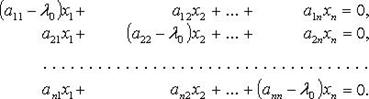
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
 где где  - соответствующие собственные значения. Теорема(Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.. Для данной матрицы - соответствующие собственные значения. Теорема(Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.. Для данной матрицы  , ,  , где Е — единичная матрица, является многочленом от , где Е — единичная матрица, является многочленом от  , который называется характеристическим многочленом матрицы A (иногда также "вековым уравнением" (secular equation)).Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение , который называется характеристическим многочленом матрицы A (иногда также "вековым уравнением" (secular equation)).Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение  имеет не нулевое решение, то имеет не нулевое решение, то  , значит матрица , значит матрица  вырождена и ее определитель вырождена и ее определитель  равен нулю. равен нулю.
Свойства:1). Для матрицы  , характеристический многочлен имеет степень , характеристический многочлен имеет степень 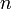 .2). Все корни характеристического многочлена матрицы являются её собственными значениями.3). Характеристические многочлены подобных матриц совпадают: .2). Все корни характеристического многочлена матрицы являются её собственными значениями.3). Характеристические многочлены подобных матриц совпадают:  . .
Билет 36. Определение и свойства скалярного произведения в абстрактном векторном пространстве
Скалярным произведением в векторном пространстве  над полем над полем 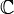 называется функция называется функция 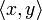 для элементов для элементов 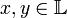 , принимающая значения в , принимающая значения в 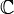 , определенная для каждой пары элементов и удовлетворяющая следующим условиям: 1).для любых трех элементов , определенная для каждой пары элементов и удовлетворяющая следующим условиям: 1).для любых трех элементов  и и 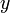 пространства пространства  и любых чисел и любых чисел  справедливо равенство справедливо равенство  (линейность скалярного произведения по первому аргументу); 2). для любых (линейность скалярного произведения по первому аргументу); 2). для любых  и и 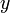 справедливо равенство справедливо равенство  , где черта означает комплексное сопряжение (эрмитова симметричность); 3). для любого , где черта означает комплексное сопряжение (эрмитова симметричность); 3). для любого  имеем имеем  , причем , причем  только при только при  (положительная определенность скалярного произведения).(линейное пространство со скалярным произведением называется евклидовым.) (положительная определенность скалярного произведения).(линейное пространство со скалярным произведением называется евклидовым.)
Элементарное определение
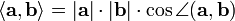
Связанные определения
В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:
- Длина вектора, под которой понимается уже упомянутая выше его евклидова норма:
 (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств). (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств). - Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):
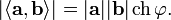 - Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
- Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
- Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.
Билет 37. Определение евклидова пространства и его примеры
Определение. Вещественное линейное пространство L называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x, yÎL сопоставлено вещественное число a = (x, y), удовлетворяющее следующим требованиям,
1. (x, y)= (y, x); 2. (x + y, z) = ((x, z) + (y, z)); 3. (ax, y)= (x,ay)= a(x, y); 4. (x, x)> 0 для всех x ¹ q; 5. (x, x)= 0, если x = q.
Любое подпространство L¢ Í L - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение.
Определение. Вещественное линейное пространство L называется евклидовым, если в нём задана положительно определённая квадратичная форма.
Примеры евклидовых пространств.
1. Геометрические векторы на плоскости L2 и в пространстве L3 с заданным скалярным произведением образуют соответствующие евклидовы пространства.
2. В арифметическом пространстве Rn мы можем ввести для элементов число
a = (x,h)= x1h1 + x2h2 +... + xnhn = xTh. Используя свойства умножения матриц
3. В пространстве функций, непрерывных на отрезке [a,b], можно ввести скалярное произведение по формуле
|



 (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.
(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных. подмножества
подмножества  линейного пространства
линейного пространства 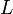 — пересечение всех подпространств
— пересечение всех подпространств  представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С1, С2, …, С(n-r), то есть,
представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С1, С2, …, С(n-r), то есть,  .ОРОСЛАУ- это общее решение однородной системы линейных алгебраических уравнений (орослау)
.ОРОСЛАУ- это общее решение однородной системы линейных алгебраических уравнений (орослау) , где
, где  - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0, 0, …, 0 и вычислив значения основных неизвестных.
- частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0, 0, …, 0 и вычислив значения основных неизвестных. и
и  . Правило, по которому каждому элементу
. Правило, по которому каждому элементу  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 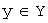 , называется ОПЕРАТОРОМ, действующим в линейных пространствах
, называется ОПЕРАТОРОМ, действующим в линейных пространствах  . Результат действия оператора
. Результат действия оператора  на элемент
на элемент  обозначают
обозначают  или
или  . Если элементы
. Если элементы  связаны соотношением
связаны соотношением  прообразом элемента
прообразом элемента  . Множество элементов линейного пространства
. Множество элементов линейного пространства  . Если
. Если 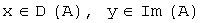 . Оператор
. Оператор  и
и 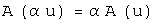 для любых
для любых  и для любого числа
и для любого числа  . Если пространства
. Если пространства  линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается
линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается 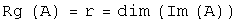 . Ядром линейного оператора называется множество элементов из
. Ядром линейного оператора называется множество элементов из 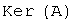 :
: 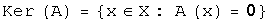 . А также:1). ранг оператора равен рангу его матрицы; 2). ядро оператора совпадает с множеством решений линейной однородной системы с 3). столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
. А также:1). ранг оператора равен рангу его матрицы; 2). ядро оператора совпадает с множеством решений линейной однородной системы с 3). столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора. Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем. и пусть
и пусть 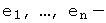 базис в
базис в  образы базисных векторов
образы базисных векторов  . Матрица
. Матрица столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейномпространстве, отвечает единственная квадратная матрица порядка n; и обратно
столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейномпространстве, отвечает единственная квадратная матрица порядка n; и обратно  с одной стороны, связывают координаты образа
с одной стороны, связывают координаты образа  к базису
к базису  . Связь между матрицей
. Связь между матрицей  оператора
оператора  и матрицей
и матрицей  этого оператора в базисе
этого оператора в базисе  задается формулой.
задается формулой.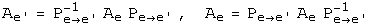

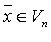 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если
, если  (
( для комплексного
для комплексного  ), такое, что
), такое, что  Число
Число  называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору. Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору. Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор 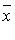 имеет координатный столбец X, то
имеет координатный столбец X, то 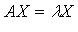 или
или  Собственные числа
Собственные числа  , где
, где  - матрица оператора f,
- матрица оператора f,  - символ Кронекера. Для каждого собственного значения
- символ Кронекера. Для каждого собственного значения 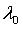 соответствующие собственные векторы могут быть найдены из матричного уравнения
соответствующие собственные векторы могут быть найдены из матричного уравнения  или соответствующей ему системы линейных уравнений
или соответствующей ему системы линейных уравнений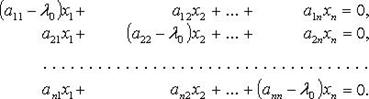
 где
где  - соответствующие собственные значения. Теорема(Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.. Для данной матрицы
- соответствующие собственные значения. Теорема(Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.. Для данной матрицы  ,
,  , где Е — единичная матрица, является многочленом от
, где Е — единичная матрица, является многочленом от  , который называется характеристическим многочленом матрицы A (иногда также "вековым уравнением" (secular equation)).Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение
, который называется характеристическим многочленом матрицы A (иногда также "вековым уравнением" (secular equation)).Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение  имеет не нулевое решение, то
имеет не нулевое решение, то  , значит матрица
, значит матрица  вырождена и ее определитель
вырождена и ее определитель  равен нулю.
равен нулю. , характеристический многочлен имеет степень
, характеристический многочлен имеет степень 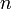 .2). Все корни характеристического многочлена матрицы являются её собственными значениями.3). Характеристические многочлены подобных матриц совпадают:
.2). Все корни характеристического многочлена матрицы являются её собственными значениями.3). Характеристические многочлены подобных матриц совпадают:  .
. над полем
над полем 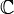 называется функция
называется функция 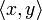 для элементов
для элементов 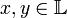 , принимающая значения в
, принимающая значения в  и
и 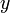 пространства
пространства  справедливо равенство
справедливо равенство  (линейность скалярного произведения по первому аргументу); 2). для любых
(линейность скалярного произведения по первому аргументу); 2). для любых  и
и  , где черта означает комплексное сопряжение (эрмитова симметричность); 3). для любого
, где черта означает комплексное сопряжение (эрмитова симметричность); 3). для любого  , причем
, причем  только при
только при  (положительная определенность скалярного произведения).(линейное пространство со скалярным произведением называется евклидовым.)
(положительная определенность скалярного произведения).(линейное пространство со скалярным произведением называется евклидовым.)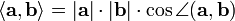
 (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
(термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).