
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 38. Квадратичные формыСодержание книги
Поиск на нашем сайте Определение квадратичной формы. Квадратичная форма переменных
Если переменные Матричная запись квадратичной формы Матрица
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если Билет 39. Канонический вид квадратичной формы Квадратичная форма называется канонической, если все
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. Способы приведения: 1. Ортогональное преобразование пространства 2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если
Затем подобную процедуру проделывают с квадратичной формой
Билет 40. Евклидова метрика — геометрическое расстояние между двумя точками в многомерном пространстве, вычисляемое по теореме Пифагора. Определение. Евклидова дистанция между точками p и q это длина отрезка
Билет 31. Базис. Размерность(тут муть!!!если попадется на мути что-нибудь…) Конечная сумма вида
называется линейной комбинацией элементов Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
Базис пространства Базис - любая упорядоченная система Обозначение: Для каждого вектора
Числа Справедливы формулы:
Матрица системы векторов Для векторов
m векторов пространства Матрица S перехода от базиса Если
или кратко:
Если
Если
Очевидно, что
Пример. Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений Решим ее методом Крамера:
Таким образом, Теперь построим X(2). Для этого придадим свободным неизвестным переменным значения x2 = 0, x4 = 1, тогда основные неизвестные найдем из системы линейных уравнений
Опять воспользуемся методом Крамера:
Получаем Так мы получили два вектора фундаментальной системы решений
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 - функция
- функция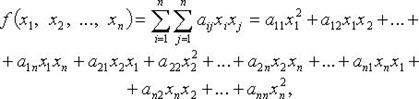
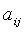 - коэффициенты квадратичной формы. Без ограничения общности считают
- коэффициенты квадратичной формы. Без ограничения общности считают 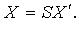 тогда
тогда
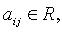 квадратичная форма называется действительной.
квадратичная форма называется действительной.
 Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве
Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве  квадратичную форму можно записать в виде
квадратичную форму можно записать в виде 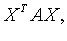 где X - координатный столбец вектора
где X - координатный столбец вектора 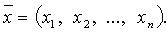 В пространстве
В пространстве 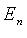 квадаратичную форму можно представить в виде
квадаратичную форму можно представить в виде  где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.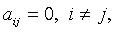 т. е.
т. е.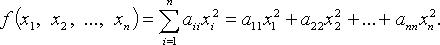
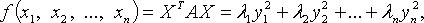 где
где  - собственные значения матрицы A.
- собственные значения матрицы A.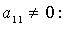

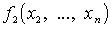 и т. д. Если в квадратичной форме все
и т. д. Если в квадратичной форме все  но есть
но есть 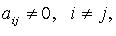 то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,
то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,  то полагаем
то полагаем 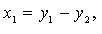

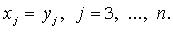 3. Метод Якоби (в случае, когда все главные миноры
3. Метод Якоби (в случае, когда все главные миноры 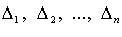 квадратичной формы отличны от нуля):
квадратичной формы отличны от нуля):
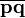 . В Декартовых координатах, если p = (p 1, p 2,…, pn) и q = (q 1, q 2,…, qn) две точки в Евклидовом пространстве, длина отрезка p q равна:
. В Декартовых координатах, если p = (p 1, p 2,…, pn) и q = (q 1, q 2,…, qn) две точки в Евклидовом пространстве, длина отрезка p q равна: 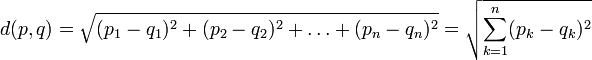
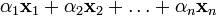
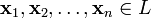 с коэффициентами
с коэффициентами  .
.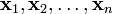 называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому элементу
называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому элементу 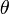 . В противном случае эти элементы называются линейно независимыми.
. В противном случае эти элементы называются линейно независимыми. 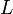 называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.
называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.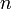 линейно независимых элементов
линейно независимых элементов 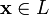 можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов: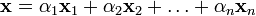 .
.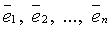 из n линейно независимых векторов пространства
из n линейно независимых векторов пространства 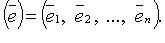
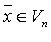 существуют числа
существуют числа  такие что
такие что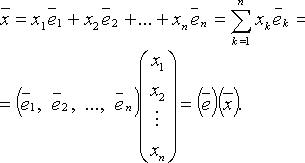
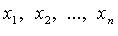 называются координатами вектора
называются координатами вектора 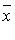 в базисе (
в базисе (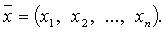
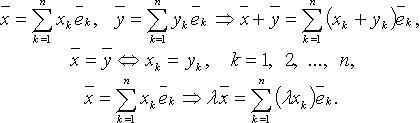
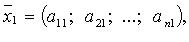
 ...,
...,  в базисе (
в базисе (
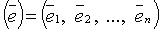 к базису
к базису  - матрица системы векторов
- матрица системы векторов 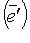 в базисе
в базисе 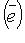
 , то:
, то: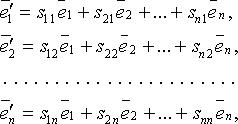
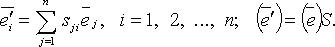
 то
то 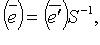 т. е.
т. е.  - матрица перехода от базиса
- матрица перехода от базиса 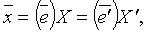 то
то 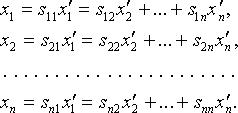
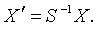
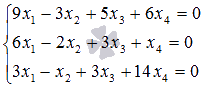 .
.
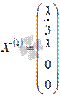 .
.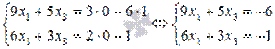 .
.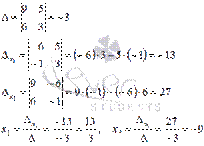
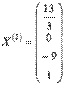 .
. и
и 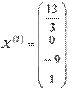 , теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений:
, теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений: , где C1 и C2 – произвольные числа.
, где C1 и C2 – произвольные числа.


