
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические операции над матрицамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Виды матриц 1) Матрица называется положительной (неотрицательной), если все ее элементы положительны (неотрицательны). 2) Матрицу, состоящую из одного столбца называют вектор-столбцом 3)Матрицу, состоящую из одной строки, будем называют вектор-строкой 4) Квадратная матрица называется верхней треугольной, если a iJ =0, i>j 5) Квадратная матрица называется нижней треугольной, если a iJ =0 i<j 6) Квадр. матрица наз-ся - симметричной если ai j =a ji 7) Квадр. Матрица наз-ся - антисимметричной матрицей, если ai j = -a ji 8) диагональной, если a iJ = 0, i ≠j 9) Диагональная матрица называется скалярной, если а11= а22 = … а2nn цифры по главной диагонали равны и!=1 10) Скалярная матрица называется единичной, если!=1 11) нулевой,все 0 12) Матрица называется верхней трапецевидной, если a iJ =0, i>j 13) нижней трапецевидной, если a iJ =0, i<j Алгебраические операции над матрицами 1) Суммой матриц A = (a iJ) и B (b iJ) одной и той же размерности размерности m x n, наз-ся матрица С (с iJ), той же размерности, элементы которой равны с iJ = a iJ + b iJ обозн. С= А+B 2) Произведением матрицы А на число k называется матрица D той же размерности элементы которой равны d iJ = k* a iJ обозн D = k A 3) Произведением A = (a ik), размерности m x p и B (b kJ)) размерности p x n наз-ся такая матрица С (с iJ) размерности m x n с iJ = ∑a ik * b kJ = a i1 b1J + a i2 b2J + … + a ip bpJ, обознач. С=АВ Число столбцов первой матрицы должно совпадать с числом строк второй, Правило "строка на столбец 4) Транспонированние матриц. Матрица AT = (aTiJ) m xn называется транспонированной по отношению к матрице A = (a iJ) m xn, если aTiJ = a Ji. При транспонир. строки <═> столбцы Свойства алгебраических операций над матрицами 1) A+B=B+A (коммутативность), 2) (A+B)+C=A+(B+C) (ассоциативность). матрицs A, B одинаковых размеров и любые числа S, t 1) (s t) A= s (t A); 2) s (A+B)= s A+ s B; 3) (s +t) A= s A+ t A. Свойства операции умножения матриц: 1) (A B) C= A (B C) (ассоциативность), 2) A (B+C)=A B+ A C, (A+B) C= A C+ B C\(дистрибутивность), 3) t(A B)= (t A) B=A (t B). Определители второго, третьего порядков и матрицы n-го порядка. Свойства определителей. Определитель – это число. Обозн. Det A, |A|, D(A) 1) det (a 11) = a 11 2) Определители второго 3) Определители третьего с помощью метода треугольника. Матрицы n-го???? Свойства определителей 1) Если в определителе есть нулевая строка (столбец), то он равен 0.
2) При перестановке двух строк (столбцов) определитель меняет знак 3) Определитель с двумя одинаковыми строками равен 0. 4) 5) 6) 7) Если одна из строк определителя есть линейная комбинация других строк, то определитель равен нулю. 8) Если к строке определителя прибавить линейную комбинацию других его строк, то определитель не изменится 9) Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения другой строки равна нулю. 10) |AT | = |A| 11) |AB|=|A| |B| 11) |AB| = |A| |B|
Алгебраическое дополнение и его свойства. Разложение определителя по строке Алгебраическое дополнение Ai j = (-1) i + j M i j | a11 a12 ……a1n | Минор: MIJ = | a21 a22 ……a2n | | …. … aiJ …...| | an1 an2 ….. ann| | a11 a12 ……a13 | A11= +(a22 a33- a23 a32) |a21 a22 ……a23 | A12 = - (a21 a33 - a23 a31) |a31 a32 ….. a33| A13 = + (a21 a32 - a22 a31) n Определитель |A| = ∑a1J A1J= a11 A11 + a12 A12 ….. a1n A1n J=1 Разложение определителя по k-ой строке Теорема о базисном миноре. Базисные строки (базисные столбцы) матрицы линейно независимы. Любая строка (любой столбец) матрицы является линейной комбинацией базисных строк (базисных столбцов). Основным методом вычисления ранга матрицы является метод элементарных преобразований (метод Гаусса) Операции, не меняющие ранга матрицы 1) Вычеркивание нулевой строки. 2) Вычеркивание одинаковых строк. 3) Перестановка строк. 4) Умножение строки на ненулевое число. 5) Прибавление к строке линейной комбинации других строк. 6) rang A Т = rang A. 7) rang (A × B)£min(rang A, rang B). 6)Система n линейных уравнений с n переменными (общий вид). Матричная форма записи системы. Совместные и несовместные, определенные и неопределенные системы НЕОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (2) A × X = B (b1) столбец (x1 ) столбец B = (b2) правых X = (x2 ) неизвестных (..) частей (…) (b m) (x n)
(a11 a12 ……a1n ) основная (a11 a12 ……a1n ) расширенная A = (a21x1 a22 …a2n) матрица A* = (a21x1 a22 …a2n) матрица …………. системы ………….. системы (a m1 a m2 … amn) (a m1 a m2 … amn) Теорема 4 (теорема Кронекера и Капелли). Неоднородная система уравнений (2) совместна тогда и только тогда, когда rangA = rangA *. Поле комплексных чисел Числовым полем называется такое числовое множество К, в котором корректны операции сложения, вычитания, умножения и деления (кроме деления на ноль).
Образуют поле множества рациональных чисел Q, действительных чисел R. Не образуют поле множества натуральных, целых, положительных, отрицательных. Операция T называется корректной относительно некоторого числового T множества К, если " a, b? K → c? K
Элементарное определение
Связанные определения В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия:
Билет 37. Определение евклидова пространства и его примеры Определение. Вещественное линейное пространство L называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x, yÎL сопоставлено вещественное число a = (x, y), удовлетворяющее следующим требованиям, 1. (x, y)= (y, x); 2. (x + y, z) = ((x, z) + (y, z)); 3. (ax, y)= (x,ay)= a(x, y); 4. (x, x)> 0 для всех x ¹ q; 5. (x, x)= 0, если x = q. Любое подпространство L¢ Í L - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение. Определение. Вещественное линейное пространство L называется евклидовым, если в нём задана положительно определённая квадратичная форма. Примеры евклидовых пространств. 1. Геометрические векторы на плоскости L2 и в пространстве L3 с заданным скалярным произведением образуют соответствующие евклидовы пространства.
2. В арифметическом пространстве Rn мы можем ввести для элементов число a = (x,h)= x1h1 + x2h2 +... + xnhn = xTh. Используя свойства умножения матриц 3. В пространстве функций, непрерывных на отрезке [a,b], можно ввести скалярное произведение по формуле Матрица системы векторов Для векторов
m векторов пространства Матрица S перехода от базиса Если
или кратко:
Если
Если
Очевидно, что
Пример. Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений Решим ее методом Крамера:
Таким образом, Теперь построим X(2). Для этого придадим свободным неизвестным переменным значения x2 = 0, x4 = 1, тогда основные неизвестные найдем из системы линейных уравнений
Опять воспользуемся методом Крамера:
Получаем Так мы получили два вектора фундаментальной системы решений
Виды матриц 1) Матрица называется положительной (неотрицательной), если все ее элементы положительны (неотрицательны). 2) Матрицу, состоящую из одного столбца называют вектор-столбцом 3)Матрицу, состоящую из одной строки, будем называют вектор-строкой 4) Квадратная матрица называется верхней треугольной, если a iJ =0, i>j 5) Квадратная матрица называется нижней треугольной, если a iJ =0 i<j 6) Квадр. матрица наз-ся - симметричной если ai j =a ji 7) Квадр. Матрица наз-ся - антисимметричной матрицей, если ai j = -a ji 8) диагональной, если a iJ = 0, i ≠j 9) Диагональная матрица называется скалярной, если а11= а22 = … а2nn цифры по главной диагонали равны и!=1 10) Скалярная матрица называется единичной, если!=1 11) нулевой,все 0 12) Матрица называется верхней трапецевидной, если a iJ =0, i>j 13) нижней трапецевидной, если a iJ =0, i<j Алгебраические операции над матрицами 1) Суммой матриц A = (a iJ) и B (b iJ) одной и той же размерности размерности m x n, наз-ся матрица С (с iJ), той же размерности, элементы которой равны с iJ = a iJ + b iJ обозн. С= А+B 2) Произведением матрицы А на число k называется матрица D той же размерности элементы которой равны d iJ = k* a iJ обозн D = k A 3) Произведением A = (a ik), размерности m x p и B (b kJ)) размерности p x n наз-ся такая матрица С (с iJ) размерности m x n с iJ = ∑a ik * b kJ = a i1 b1J + a i2 b2J + … + a ip bpJ, обознач. С=АВ Число столбцов первой матрицы должно совпадать с числом строк второй, Правило "строка на столбец
4) Транспонированние матриц. Матрица AT = (aTiJ) m xn называется транспонированной по отношению к матрице A = (a iJ) m xn, если aTiJ = a Ji. При транспонир. строки <═> столбцы
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.119 (0.009 с.) |

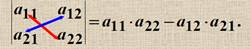


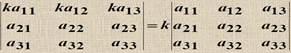
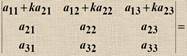
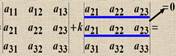

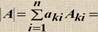
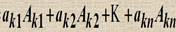
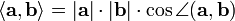
 (термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
(термин 'длина' обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
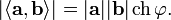
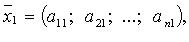
 ...,
...,  в базисе (
в базисе (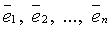 ) - матрица
) - матрица
 линейно независимы тогда и только тогда, когда rank A = m.
линейно независимы тогда и только тогда, когда rank A = m.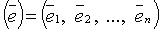 к базису
к базису  - матрица системы векторов
- матрица системы векторов 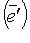 в базисе
в базисе 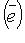
 , то:
, то: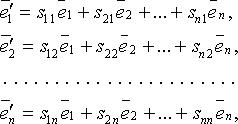
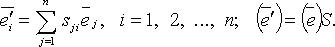
 то
то 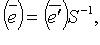 т. е.
т. е.  - матрица перехода от базиса
- матрица перехода от базиса 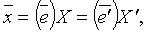 то
то 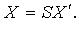 В развернутой записи:
В развернутой записи: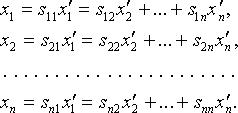
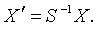
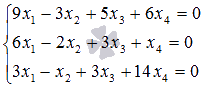 .
.
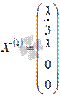 .
.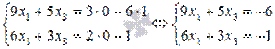 .
.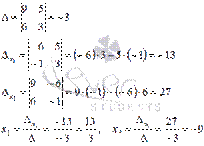
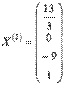 .
. и
и 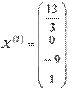 , теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений:
, теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений: , где C1 и C2 – произвольные числа.
, где C1 и C2 – произвольные числа.


