
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над множествамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейные операции над множествами
Линейными действиями над матрицами называются сложение и вычитание матриц, умножение матрицы на число. Сложение и вычитание матриц определяются только для матриц одинаковых размеров. Определение 1.3. Суммой двух матриц
Сумма двух матриц A и B обозначается A+B=C. Под суммой A+B+C трех матриц A, B и С понимается матрица, полученная в результате последовательного сложения этих матриц, т.е. A+B+C =(A+B) +C. Таким же образом можно определить сумму матриц для большего числа слагаемых. Аналогично определяется разность матриц. Определение 1.4. Произведением матрицы
Пример 1.1. Найти матрицу Решение.
Определение 1.5. Матрица Таким образом, разность двух матриц можно определить так: Линейные операции над матрицами обладают следующими свойствами, которые примем без доказательства: 1. 2. 3. 4. 9. 10. где A, B и С – матрицы одних и тех же размеров; O – нулевая матрица, (- A) – матрица, противоположная матрице A; a и b - любые действительные числа.
1.3. Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
Определение 1.6. Две матрицы A и B называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается A~ B. При помощи элементарных преобразований любую матрицу можно привести к эквивалентной ей ступенчатой матрице. Пример 1.2. Привести данную матрицу к трапециевидной:
Решение. Сначала переставим местами первую и вторую строки, т.к. первый элемент второй строки равен 1.
[первую строку умножаем на (-2) и складываем со второй строкой; первую строку умножаем на 3 и складываем с четвертой строкой]
~
[делим третью строку на 2 и переставляем вторую и третью строки местами]
~
[вторую строку умножаем на (-7) и складываем с третьей строкой; вторую строку умножаем на 5 и складываем с четвертой строкой]
~
[сначала разделим третью строку на 18, а потом умножим на 21 и сложим с четвертой строкой]
~
Произведение матриц
Определение 1.7. Матрицы A и B называются согласованными, если число столбцов («ширина») первой матрицы равно числу строк («высоте») второй матрицы. Определение 1.8. Произведением матрицы
Произведение AB рассматривают как результат умножения матрицы A на матрицу B слева или умножение матрицы B на матрицу A справа.
Пример 1.3. Найти произведения AB и BA для следующих матриц:
Решение. Так как матрица A имеет размерность 2´3, а матрица B – размерность 3´2, то эти матрицы согласованны и результатом произведения AB будет матрица C размерности 2´2.
Так как матрица B имеет размерность 3´2, а матрица A - размерность 2´3, то эти матрицы согласованны и результатом произведения будет матрица D размерности 3´3.
, Надо отметить, что результатом произведения двух ненулевых матриц может быть нулевая матрица. Как видно из примера 1.3. AB ¹ BA. В случае, когда AB = BA, матрицы A и B называются перестановочными, или коммутативными.
Произведение матриц обладает следующими свойствами, которые примем без доказательства: 1. 2. 3. 4. 5. где A, B и С – согласованные матрицы; a и b - любые действительные числа.
Транспонирование матриц
Определение 1.9. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной. Матрицу, транспонированную относительно матрицы A, обозначают AТ. Таким образом, если
Отмети, что если A – матрица размера m ´ n, то матрица AТ имеет размер n ´ m. Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы.
2. ОПРЕДЕЛИТЕЛИ
2.1. Основные понятия
Квадратной матрице A порядка n можно сопоставить число Для матрицы первого порядка, т.е. Определение 2.1. Определителем 2-го порядка матрицы
Пример 2.1. Найти определители 2-го порядка: , Определение 2.2. Определителем 3-го порядка матрицы
Заметим, что каждое слагаемое алгебраической суммы в правой части представляет собой произведение элементов определителя, взятых по одному и только по одному из каждой строки и каждого столбца. Этому произведению приписывается соответствующий знак. Чтобы помнить, какие произведения следует брать со знаком плюс, какие – со знаком минус, можно пользоваться правилом, схематически изображенным на рисунке.
«+» «-»
Пример 2.2. Найти определитель 3-го порядка.
, Правило, по которому находиться определитель 3-го порядка (определение 2.2.), называется правилом треугольника (правило Саррюса). Но для более удобного вычисления определителя 3-го порядка можно применить правило приписывания к определителю справа первых двух ее столбцов.
«-» «-» «-» «+» «+» «+»
Определитель матрицы A также называют детерминантом. Правило вычисления детерминанта для матрицы n -го порядка является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда, который рассмотрим несколько позже. При этом заметим, что определители невысоких порядков (1-го, 2-го и 3-го) желательно вычислять согласно определению.
Определение 2.3. Минором Mij некоторого элемента Например, для определителя Определение 2.4. Алгебраическим дополнением Aij некоторого элемента
Например, для определителя Каждый определитель состоит из строк и столбцов. В дальнейшем строки и столбцы будем называть рядами определителя.
Определение 2.5. Определителем матрицы n-го порядка
называется число, равное сумме произведений элементов его произвольного ряда на их алгебраические дополнения, т.е. справедлива одна из формул:
называемая разложением определителя по i-ой строке, или
называемая разложением определителя по j-ому столбцу. Пример 2.3. Найти определитель 3-го порядка, используя разложение по второй строке.
Свойства определителей
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств докажем с использованием определителей 3-го порядка. Свойство 1. При транспонировании значение определителя не изменяется.
Доказательство. В определителе 3-го порядка каждую строку заменим столбцом с тем же номером, получим новый определитель.
= [полученное выражение можно сравнить с определением 2.2] = , Свойство 2. Если поменять местами два параллельных ряда определителя, то он изменит знак на противоположный.
Свойство 3. Определитель с двумя одинаковыми параллельными рядами равен нулю.
Свойство 4. Если определитель содержит нулевой ряд, то его значение равно нулю.
Свойство 5. Если какой-либо ряд содержит общий множитель, то его можно вынести за знак определителя Доказательство. Пусть, например, в определителе элементы второй строки имею множитель k, тогда
Свойство 6. Определитель, у которого элементы двух параллельных рядов соответственно пропорциональны, равен нулю.
Свойство 7. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. Доказательство. Пусть, например, в определителе элементы второго столбца представляют собой сумму двух слагаемых, тогда
[раскроим скобки и сгруппируем слагаемые]
, Свойство 8. Если к элементам какого-либо ряда определителя прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число, то его значение не изменится.
Свойство 9. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Доказательство. Покажем, например, что
,
Решение. 1) Воспользуемся разложением определителя по второй строке, поскольку в этой строке один элемент нулевой. Получаем
2) Воспользуемся приведением определителя к треугольному виду. Умножим вторую строку на (-2) и прибавим к первой строкой, умножим вторую строку на (-3) и прибавим к третьей, умножим вторую строку на (-4) и прибавим к четвертой. Получаем
[складываем вторую и третью строку, вторую строку умножаем на 2 и складываем с четвертой строкой]
[умножаем третью строку на (-11/8) и складываем с четвертой строкой]
3) Используем метод эффективного понижения порядка. Умножим первый столбец на (-2) и прибавим к третьему столбцу, умножим первый столбец на (-1) и прибавим к четвертому столбцу.
[к первой строке прибавим вторую; первую строку умножим на 2 и прибавим третью строку]
= ,
3. ОБРАТНАЯ МАТРИЦА
3.1. Теорема существования обратной матрицы
Определение 3.1. Квадратная матрица A называется невырожденной, если ее определитель Определение 3.2. Матрицей, присоединенной к матрице A, называется матрица вида
где Определение 3.3. Матрица
где E – единичная матрица того же порядка, как и матрица A.
Матрица
Пример 3.1. Показать,что матрица A является обратной для матрицы B, если
Решение. Найдем произведение матриц A и B.
Аналогично , Теорема 3.1. Для невырожденной матрицы A существует единственная обратная матрица
где
Теорему 3.1 примем без доказательства.
Пример 3.2. Найти Решение. 1) Находим определитель матрицы A.
Матрица A – невырожденная, значит, существует ей обратная. 2) Находим алгебраические дополнения элементов матрицы A.
Составляем матрицу, присоединенную к матрице A.
3) Находим
Сделаем проверку:
,
Формулы Крамера
Рассмотрим систему n линейных уравнений с n неизвестными
Определитель системы обозначим
Обозначим через
где k - одно из чисел 1, 2, …, n. Теорема 5.1. (Теорема Крамера) Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам
где
Теорему 5.1. примем без доказательства. Формулы (5.4) называются формулами Крамера. Из теоремы Крамера следует: если однородная система имеет решение, то ее определитель
Пример 5.2. Решить СЛУ по формулам Крамера
Решение. Находим
Далее получаем решение:
,
Метод Гаусса
Метод Гаусса является исторически первым наиболее распространенным точным методом решения системы линейных уравнений. Сущность этого метода состоит в том, что посредством элементарных преобразований данная система приводится к специальному виду, из которого все решения системы непосредственно усматриваются.
Рассмотрим СЛУ (5.5), содержащую из m уравнений и n неизвестных:
Метод Гаусса или метод последовательного исключения неизвестных, применяемый для решения системы (5.5), состоит в следующем. Пусть в системе коэффициент
где Предполагая, что 1)
где 2)
где 3)
где Запись системы, полученной после преобразований, называют ступенчатой (в частности, при Система (5.7) имеет единственное решение. Из последнего уравнения Система (5.8) имеет бесчисленное множество решений. Из последнего уравнения можно выразить одно из неизвестных (например,
Полученная система представляет собой общее решение исходной системы. Неизвестные Система (5.9) не имеет решений, так как эта система несовместна, т.е. никакие значения неизвестных не могут удовлетворять ее последнему уравнению. Итак, метод последовательного исключения неизвестных применим к любой системе линейных уравнений. Решая систему этим методом, преобразования можно совершать не над самими уравнениями, а над расширенной матрицей.
Пример 5.3. Решить СЛУ методом Гаусса:
Решение. Составляем расширенную матрицу:
Сначала поменяем местами первую и третью строки, получаем:
Поскольку во второй строке первый элемент равен нулю, то элементы второй строки не изменяем. Умножаем элементы первой строки на
Теперь поменяем местами вторую и третью строки:
Умножаем элементы второй строки на
По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
Из последнего уравнения находим , Пример 5.4. Решить систему уравнений
Решение. Составляем расширенную матрицу:
Сначала поменяем местами первую и третью строки, чтобы первый элемент (для удобства) был равен 1. Этот элемент будет разрешающим.
[вторую и третью строки умножим на (-1)] ~ По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
Из последнего уравнения находим , Пример 5.5. Решить систему уравнений
Решение. Составляем расширенную матрицу и преобразуем ее:
Система несовместна, так как последняя матрица содержит строку, соответствующую уравнению, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля. , Пример 5.6. Решить систему уравнений
Решение. Составляем расширенную матрицу и преобразуем ее:
~ Исходная система свелась к ступенчатой:
Из последнего уравнения за базисную неизвестную выберем, например,
Таким образом, получаем общее решение системы:
Пусть
где ,
5.3.Исследование СЛУ
Как уже отмечалось, метод Гаусса применим к любой системе линейных уравнений. Этот метод позволяет выяснить, совместна ли данная система; с его помощью находятся все решения совместной линейной системы. Исследование систем линейных уравнений можно осуществлять с помощью других методов, основанных на теоремах, которые приводятся без доказательства.
Линейные операции над множествами
Линейными действиями над матрицами называются сложение и вычитание матриц, умножение матрицы на число. Сложение и вычитание матриц определяются только для матриц одинаковых размеров. Определение 1.3. Суммой двух матриц
Сумма двух матриц A и B обозначается A+B=C. Под суммой A+B+C трех матриц A, B и С понимается матрица, полученная в результате последовательного сложения этих матриц, т.е. A+B+C =(A+B) +C. Таким же образом можно определить сумму матриц для большего числа слагаемых. Аналогично определяется разность матриц. Определение 1.4. Произведением матрицы
Пример 1.1. Найти матрицу Решение.
Определение 1.5. Матрица Таким образом, разность двух матриц можно определить так: Линейные операции над матрицами обладают следующими свойствами, которые примем без доказательства: 1. 2. 3. 4. 9. 10. где A, B и С – матрицы одних и тех же размеров; O – нулевая матрица, (- A) – матрица, противоположная матрице A; a и b - любые действительные числа.
1.3. Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
Определение 1.6. Две матрицы A и B называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается A~ B. При помощи элементарных преобразований любую матрицу можно привести к эквивалентной ей ступенчатой матрице. Пример 1.2. Привести данную матрицу к трапециевидной: | |||||||
|
| Поделиться: |

 и
и  одной размерности называется матрица
одной размерности называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов исходных матриц, т.е.
той же размерности, каждый элемент которой равен сумме соответствующих элементов исходных матриц, т.е. . (1.2)
. (1.2) . (1.3)
. (1.3)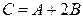 , где
, где  ,
, 
 ,
, называется противоположной матрице A.
называется противоположной матрице A. .
. ; 5.
; 5. 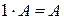 ;
; ; 6.
; 6.  ;
;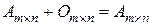 ; 7.
; 7.  ;
; ; 8.
; 8.  ;
; ;
; .
.
 ~
~ ~
~ ~
~ ~
~ .,
., на матрицу
на матрицу  называется матрица
называется матрица  , каждый элемент которой определяется следующим образом:
, каждый элемент которой определяется следующим образом: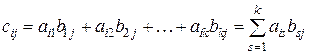 . (1.4)
. (1.4) и
и  .
.
 .
.
 .
. , единичная матрица E играет роль единицы;
, единичная матрица E играет роль единицы; , нулевая матрица O играет роль нуля;
, нулевая матрица O играет роль нуля; ;
; ; 6.
; 6.  ;
; ; 7.
; 7.  .
.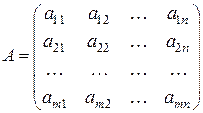 , то
, то  (1.5)
(1.5) (или
(или  , или
, или  ), называемое ее определителем.
), называемое ее определителем. , определителем будет
, определителем будет  .
. называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу . (2.1)
. (2.1) .
. называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу
называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу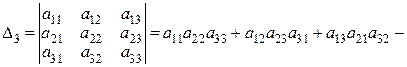
 (2.2)
(2.2)
 .
.
 называется определитель, полученный из исходного вычеркиванием i -ой строки и j -го столбца, на пересечении которых находится выбранный элемент.
называется определитель, полученный из исходного вычеркиванием i -ой строки и j -го столбца, на пересечении которых находится выбранный элемент. минор элемента
минор элемента  будет
будет  , а минор элемента
, а минор элемента  будет
будет  . Для определителя 2-го порядка
. Для определителя 2-го порядка  минор элемента
минор элемента  .
. , т.е.
, т.е. . (2.3)
. (2.3)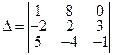 алгебраическое дополнение элемента
алгебраическое дополнение элемента  , а алгебраическое дополнение элемента
, а алгебраическое дополнение элемента  .
.
 , (2.4)
, (2.4) , (2.5)
, (2.5) ,
,
 .
.
 ,
,



 .
. .
.


 .
.

 .
.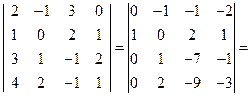 [поменяем местами первую и вторую строку]
[поменяем местами первую и вторую строку] 

 .
.
 .
. . В противном случае матрица A называется вырожденной или особенной.
. В противном случае матрица A называется вырожденной или особенной. ,
, - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя).
данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя). называется обратной матрице A, если выполняется условие
называется обратной матрице A, если выполняется условие , (3.1)
, (3.1) .
. .
.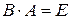 . Следовательно, матрица A является обратной для B.
. Следовательно, матрица A является обратной для B. , (3.2)
, (3.2) - матрица, присоединенная к матрице A.
- матрица, присоединенная к матрице A. .
. .
. .
. .
. .
.
 .
. :
: .
. определитель, полученный заменой в определителе
определитель, полученный заменой в определителе  столбца из коэффициентов при неизвестной
столбца из коэффициентов при неизвестной  столбцом свободных членов системы, т.е.
столбцом свободных членов системы, т.е. ,
, , (5.4)
, (5.4) .
. :
: ;
;  ;
; ;
;  .
. .
. . (5.5)
. (5.5) , который называется разрешающим коэф-фициентом. Если
, который называется разрешающим коэф-фициентом. Если  , то на первое место можно поставить уравнение, в котором коэффициент при неизвестной
, то на первое место можно поставить уравнение, в котором коэффициент при неизвестной  отличен от нуля. Умножаем первое уравнение системы (5.5) на
отличен от нуля. Умножаем первое уравнение системы (5.5) на  и прибавляем ко второму, получаем уравнение, в котором коэффициент при
и прибавляем ко второму, получаем уравнение, в котором коэффициент при  и прибавляем к третьему, получаем уравнение, также не содержащее члена с
и прибавляем к третьему, получаем уравнение, также не содержащее члена с  -ом уравнении коэффициент при
-ом уравнении коэффициент при  , (5.6)
, (5.6) - некоторые новые коэффициенты при неизвестных,
- некоторые новые коэффициенты при неизвестных,  - новые свободные члены.
- новые свободные члены. , который становится разрешающим коэффициентом, и, оставляя неизменными первые два уравнения системы (5.6), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при
, который становится разрешающим коэффициентом, и, оставляя неизменными первые два уравнения системы (5.6), преобразуем ее так, чтобы в каждом из остальных уравнений коэффициент при  обратился в нуль. Продолжая этот процесс, систему (5.6) можно привести к одной из следующих систем:
обратился в нуль. Продолжая этот процесс, систему (5.6) можно привести к одной из следующих систем: , (5.7)
, (5.7) и
и  .
. , (5.8)
, (5.8) и
и  .
. , (5.9)
, (5.9) .
. находим
находим  :
:  . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим  , затем из третьего от конца -
, затем из третьего от конца -  . Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (5.5) к одному из видов (5.7), (5.8) или (5.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (5.7) с целью получения значений неизвестных – обратным ходом.
. Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (5.5) к одному из видов (5.7), (5.8) или (5.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (5.7) с целью получения значений неизвестных – обратным ходом. неизвестных (
неизвестных ( ), входящих в это уравнение. Полученное значение
), входящих в это уравнение. Полученное значение  через эти неизвестные и т.д. И, наконец, выражаем
через эти неизвестные и т.д. И, наконец, выражаем  . (5.10)
. (5.10) - базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (5.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании.
- базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (5.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании. .
. .
. и складываем с соответствующими элементами третьей строки:
и складываем с соответствующими элементами третьей строки: .
. .
. и складываем с соответствующими элементами третьей строки, получаем:
и складываем с соответствующими элементами третьей строки, получаем: .
. .
. , из второго –
, из второго –  и из первого –
и из первого –  . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение 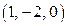 .
. .
. .
. ~
~  ~
~ ~
~  .
. .
. , из второго –
, из второго –  и из первого –
и из первого –  . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение  .
. .
. ~
~  ~
~  .
. .
. ~
~  ~
~  ~
~ .
. .
. :
:  . Подставляем
. Подставляем  .
. .
. , где
, где  - любые действительные числа. Тогда получаем следующее решение
- любые действительные числа. Тогда получаем следующее решение ,
,


