
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы вычисления ранга матрицыСодержание книги
Поиск на нашем сайте
1) Метод окаймляющих миноров. Пусть в матрице найден минор k -го порядка M, отличный от нуля. Рассмотрим лишь те миноры (k +1)-го порядка, которые содержат в себе (окаймляют) минор M: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k +1)-го порядка, и вся процедура повторяется. 2) Метод элементарных преобразований основан на том факте, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования, матрицу можно привести к ступенчатому виду. Число ненулевых строк равняется рангу матрицы. Пример 4.2. Найти ранг матрицы двумя способами:
Решение. 1) Найдем ранг матрицы, используя метод окаймляющих миноров. Данная матрица содержит ненулевые элементы, например,
Далее рассматриваем минор 3-го порядка:
Для данной матрицы можно составить 10 миноров 3-го порядка. Все они равны нулю. Поскольку существует хотя бы один минор 2-го порядка, неравный нулю, то 2) Найдем ранг матрицы, используя метод элементарных преобразований. Сначала переставим строки: вторую строку поставим первой строкой, умножив на (-1); пятую строку – второй; а первую – пятой. Получаем
Произведя последовательно элементарные преобразования, будем иметь
Так как последняя матрица содержит две ненулевые строки, то
5. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
5.1. Основные понятия
Определение 5.1. Системой линейных уравнений (СЛУ), содержащей m уравнений и n неизвестных, называется система вида
где числа Коэффициенты обозначаются буквой a с двумя индексами i и j; первый индекс (i) указывает номер уравнения, второй (j) – номер неизвестной, к которой относится данный коэффициент. Число m уравнений может быть больше, равно или меньше числа n неизвестных. Определение 5.2. СЛУ называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, линейная система называется однородной. Определение 5.3. Решением СЛУ называется упорядоченная совокупность n чисел:
подстановка которых вместо
Всякое решение системы можно записать в виде матрицы-столбца
Допускается и такая запись:
Определение 5.4. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Отметим, что однородная система всегда совместна, так как она имеет нулевое решение
Определение 5.5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Решить СЛУ – это значит выяснить, совместна она или несовместна. Если система совместна, найти все ее решения.
Определение 5.6. Две системы называются эквивалентными (равносильными), если любое решение одной из них является также решением другой и обратно, т.е. если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными. Элементарными преобразованиями линейной системы называются следующие преобразования: 1) перестановка местами двух уравнений системы; 2) умножение уравнения системы на число, отличное от нуля; 3) прибавление к одному уравнению системы другого ее уравнения, умноженного на любое число, отличное от нуля.
Линейную систему можно записать в матричной форме. Рассмотрим СЛУ (5.1). Матрица, составленная из коэффициентов линейных уравнений системы
называется основной матрицей системы. Матрица, полученная из основной присоединением столбца из свободных членов
называется расширенной матрицей системы. Матрицы-столбцы, составленные из неизвестных и свободных членов имеют вид:
Поскольку матрица A согласована с матрицей X, то можно найти произведение
Элементы этой матрицы-столбца являются левые части уравнения системы (5.1), поэтому на основании определения равенства матриц
Таким образом, СЛУ (5.1.) можно записать в идее одного матричного уравнения (5.2.), которое называется матричной формой.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.229.1 (0.006 с.) |

 .
. . Переходим к минору 2-го порядка, который окаймляет минор
. Переходим к минору 2-го порядка, который окаймляет минор  :
: .
. .
. .
.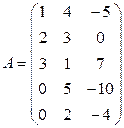 .
. .
. .,
.,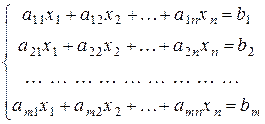 , (5.1)
, (5.1) называются коэффициентами системы, числа
называются коэффициентами системы, числа  - свободными членами.
- свободными членами. ,
, соответственно
соответственно  обращает в тождество каждое из уравнений этой системы.
обращает в тождество каждое из уравнений этой системы. .
. или
или  .
.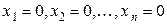 , которое называется нулевым или тривиальным.
, которое называется нулевым или тривиальным.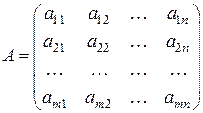

 ,
, 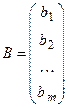 .
.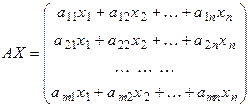 .
. (5.2)
(5.2)


