Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объединения. Операции, представление. Сложность операций.Содержание книги
Поиск на нашем сайте В Паскале – нет В Си – Union <имя> { T1 S1; T2 S2; … Tn Sn; } Все элементы начинаются с одно и того же места в памяти (если присваиваем новое значение элементу объединения, то перезаписываем любое предыдущее присваивание). Объединение может хранить значение только для одного элемента в каждый момент времени. Пример: иллюстрирует использование объединения distance. Сначала программа присваивает значение элементу miles и выводит это значение. Затем программа присваивает значение элементу meters. При этом значение элемента miles теряется: union distance { walk.miles = 5; Характеристики: 1)Размер – максимальный из размеров компонент sizeof (union) = max(sizeof Ti); 2)Мощность – мощность максимального типа #union = #max(Ti). Операции: 1)Индексация по имени; 2)Присваивание А=В через memcpy; 3)Сравнение А==В через memcmp(A, B, sizeof B); Объединения применяют для записей с вариантами (если в анкете, то каждый последующий порос зависит от предыдущего ответа).
МНОЖЕСТВА. ОПЕРАЦИИ, СПОСОБЫ ПРЕДСТАВЛЕНИЯ, СЛОЖНОСТЬ ОПЕРАЦИЙ. В языке Паскаль множество — составной тип данных, хранящий информацию о присутствии в множестве объектов любого счетного типа. T: set of Tbase Характеристики: 1)Мощность множества – количество множеств, котрое можно построить на основе базового типа Например, множество (1, 2): можно построить пустое множество, (1), (2), (1,2) – всего 4. 2)Размер – один бит на элемент sizeof set = (#Tbase)/8. Т. е. представление одного элемента множества – один бит, имеем дело с битовыми строками Операции: 1)Индексации нет; 2)Присваивание А=В 3) Сравнение ==,!=, а так же включение A <= B; 4)Проверка на вхождение a in B – истина, если а есть в В; ложь, если элемента а в И не было; 5)Объединение (+), Пересечение (*), Вычитание (-). Примеры множеств – множество, куда записывается алфавит входного сообщения или множество для обработки команд (см. конспект). Представление в памяти – стр. 46. Когда размерность битовой строки не превышает длинны машинного слова, представление в виде множеств будет максимально эффективно.
ПОСЛЕДОВАТЕЛЬНОСТИ ВКРАТЦЕ Последовательность - бесконечная структура данных с последовательным доступом, все элементы последовательности имеют один и тот же базовый тип. T: sequence of Tbase Операции: 1)Взятие read x=read() – берем текущий элемент данной последовательности; 2)Добавление (ограничение только по объему памяти) write(x) – добавляем х в конец последовательности; 3)Переход в начало rewind (). Обычно представляет собой однородную структуру, подобную массиву. Но существенная разница в том, что у массива число элементов зафиксировано в его определении, а у последовательности – нет. То есть оно может меняться во время выполнения программы. Хотя каждая последовательность в любой момент времени имеет конкретную конечную длину, мы должны считать мощность последовательного типа бесконечной, т.к. нет никаких ограничений на потенциальную длину последовательностей. Прямое следствие переменной длины – невозможность отвести фиксированный объем памяти под переменные-последовательности. Поэтому память выделяется в ходе выполнения программы, в частности, когда последовательность растет. Таким образом, для работы с последовательностями необходима динамическая схема выделения памяти. Основное правило работы с последовательностями: доступ к элементам осуществляется строго в порядке их следования, а порождается последовательность присоединением новых элементов к ее концу. Следствие – невозможность прямого доступа к элементам, за исключением того элемента, который доступен для просмотра в данный момент. Это и является главным отличием последовательностей от массивов.
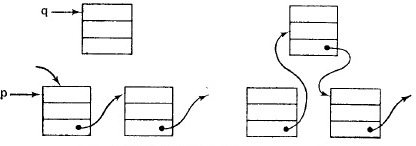
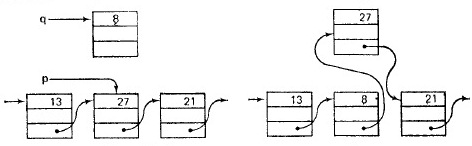
ЛИНЕЙНЫЕ СПИСКИ Линейный список – это множество элементов хранения с заданным отношением строгого порядка, определяющим следование элементов в множестве. Требование строгого порядка вызвано тем, что с каждым элементом линейного списка при хранении связан конкретный физический адрес. Линейный список – либо пустой список, либо элемент, ссылающийся на линейный список. Описание: struct { Tdata data; // поле данных какого-либо произвольного типа struct ls *next; // ls – линейный список, next – указатель на ls (структуру л. с.) } – ссылаемся на структуру, пока ее описание не закончено. Операции: 1)Вставка Имеется указатель на некий элемент p, нужно вставить элемент q: a) после р (через присваивание – не требует сложных операций и памяти)
b) до р (используем случай а, а затем меняем местами
2)Удаление из списка a) после p: p.next=q.next; free(q); - перенаправляем указатель, освобождаем память. b) до р переписать информацию из p.next в q.next, удалить p.next, используя случай а. Операции удаления/вставки занимают время О(1) и не зависят от длины линейного списка, имеют преимущества по сравнению. Операции поиска и индексации (доступ к элементам) – O(n). Пример применения списка – подсчет количества всех переменных в программе: main() { int i; for (i=0; i<N; i++) {} } Алгоритм: вносим первую встретившуюся переменную в линейный список, увеличиваем ее счетчик, в дальнейшем сверяем каждую прочитанную, есть ли такая в списке, если нет, то добавляем ее в список и увеличиваем ее счетчик, иначе увеличиваем счетчик уже имеющейся в списке переменной, завершаем список.
Двунаправленный линейный список – первый указатель связывает данный элемент со следующим, а второй - с предыдущим. Интересным свойством такого списка является то, что для доступа к его элементам вовсе не обязательно хранить указатель на первый элемент. Достаточно иметь указатель на любой элемент списка. Первый элемент всегда можно найти по цепочке указателей на предыдущие элементы, а последний - по цепочке указателей на следующие. Но наличие указателя на заголовок списка в ряде случаев ускоряет работу со списком. Циклические списки также как и линейные бывают однонаправленными и двунаправленными. Основное отличие циклического списка состоит в том, что в списке нет пустых указателей NULL. Последний элемент списка содержит указатель, связывающий его с первым элементом. Для полного обхода такого списка достаточно иметь указатель только на текущий элемент. В двунаправленном циклическом списке система указателей аналогична системе указателей двунаправленного линейного списка. ОЧЕРЕДИ.
Очередь – рекурсивный безразмерный набор данных, построенный по принципу FIFO. Операции: 1)put(x); - поставить элемент в очередь Занесение элемента в очередь реализуется как добавлению элемента в конец списка. 2)x=get(); - взять элемент из очереди Процедура извлечения элемента из очереди аналогична удалению элемента из начала списка. Реализация очереди: - Первый способ представляет очередь в виде массива и двух целочисленных переменных start и end. Обычно start указывает на голову очереди, end — на элемент, который заполнится, когда в очередь войдёт новый элемент. При добавлении элемента в очередь в q[end] записывается новый элемент очереди, а end уменьшается на единицу. Если значение end становится меньше 1, то мы как бы циклически обходим массив и значение переменной становится равным n. Извлечение элемента из очереди производится аналогично: после извлечения элемента q[start] из очереди переменная start уменьшается на 1. С такими алгоритмами одна ячейка из n всегда будет незанятой (так как очередь с n элементами невозможно отличить от пустой), что компенсируется простотой алгоритмов. Преимущества данного метода: возможна незначительная экономия памяти по сравнению со вторым способом; проще в разработке. Недостатки: максимальное количество элементов в очереди ограничено размером массива. При его переполнении требуется перевыделение памяти и копирование всех элементов в новый массив. - Линейный список, сложность операции O(1) Второй способ основан на работе с динамической памятью. Очередь представляется в качестве линейного списка, в котором добавление/удаление элементов идет строго с соответствующих его концов. Преимущества данного метода: размер очереди ограничен лишь объёмом памяти. Недостатки: сложнее в разработке; требуется больше памяти; при работе с такой очередью память сильнее фрагментируется; работа с очередью несколько медленнее.
СТЕКИ.
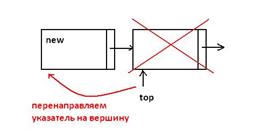
Стек – это линейный список, в котором добавление новых элементов и удаление существующих производится только с одного конца, называемого вершиной стека (упорядоченный набор элементов, в котором размещение новых элементов и удаление осуществляется только с одного конца.). Доступ к элементам организован по принципу LIFO. Операции: 1)push(x) – «втолкнуть» элемент в список Занесение элемента в стек производится аналогично вставке нового элемента в начало списка. Процедура занесения элемента в стек должна содержать два параметра: первый задает вершину стека, в который нужно занести элемент, второй – заносимое значение элемента стека.
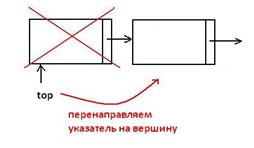
2)x=pop(x) – взять элемент из списка В результате выполнения этой операции некоторой переменной i должно быть присвоено значение первого элемента стека, и значение указателя на начало списка должно быть перенесено на следующий элемент стека.
Стеки применяются для вызова процедур (хранение локальных переменных и адреса возврата), рекурсии, обеспечения перебора с возвратом (8 ферзей). Стеки широко применяются в вычислительной технике. Например, для отслеживания точек возврата из подпрограмм используется стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров. Языки программирования высокого уровня также используют стек вызовов для передачи параметров при вызове процедур. Пример применения – задача с последовательностью открытых и закрытых скобок (см. конспект). Реализация стека: - линейный список, сложность операций О(1) - Массив
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

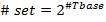 .
.