
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические струкутуры данных. Работа динамической памяти в C.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Динамические структуры данных Во многих задачах требуется использовать данные, у которых конфигурация, размеры и состав могут меняться в процессе выполнения программы. Для их представления используют динамические информационные структуры. К таким структурам относят:
Они отличаются способом связи отдельных элементов и/или допустимыми операциями. Динамическая структура может занимать несмежные участки оперативной памяти. Динамические структуры широко применяют и для более эффективной работы с данными, размер которых известен, особенно для решения задач сортировки. Использование динамических величин предоставляет программисту ряд дополнительных возможностей. Во-первых, подключение динамической памяти позволяет увеличить объем обрабатываемых данных. Во-вторых, если потребность в каких-то данных отпала до окончания программы, то занятую ими память можно освободить для другой информации. В-третьих, использование динамической памяти позволяет создавать структуры данных переменного размера. Память:
Динамическое распределение памяти Функция p=выделить(N) возвращает указатель на объект памяти длиной N, В Си – p=new(N) (неопределенный тип указателя). Проблемы: 1) Типизация указателя. В языка строгой типизации int *p и char*g - не эквивалентны => необходимо преобразование типа. 2) Освобождение выделяемой памяти · Явный механизм (программист) – функция уничтожить(р); · Нет явного механизма (ОС) – уничтожается, когда отсутствуют ссылки на объект, можно осуществлять через таймер, по завершению программв, при переполнении. 3) Проблема висящих объектов (когда один динамический объекс ссылается на другой динамический объект) В памяти остаются объекты с отсутствием ссылок. Уничтожив этот объект, можно потерять ссылки на все его подобъекты. 4) Проблема висящих указателей (остются ссылки на уничтоженные объекты); 5) Фрагментация памяти heap
Уничтожим р3 и р5 – на новый объект хватит памяти, но не будет цельного куска. Правила при работе с динамической памятью при наличии явных механизмов уничтожения: 1) Не допускать наличие висящих объектов. Для этого сначала надо уничтожить все вложенные объекты. 2) Не допускать висящих ссылок, т. е. после уничтожения объекта уничтожить и ссылку на него - p=NULL. 3) Минимизировать фрагментацию. Для этого нужно уничтожать объекты в порядке обратном порядку их создания: р5 – р4 – р3. Реализация механизма динамической памяти в C: 1) Выделение динамической памяти через функцию void *malloc(size_t size). Например, если нужно 10 элементов массива, то: int A; A=(int*)malloc(10 * sozeof(int)). Размер требуемой памяти size_t size может быть больше, чем требуется (для выравнивания) 2) Функция void *calloc(size_t num, size_t size); все значения в полученной памяти нулевые. 3) void free (void*p) указатель указывает на ранее захваченный блок памяти операциями malloc, calloc, realloc, т. е. число освобождаемых байтов = числу байтов, полученных при захвате преобразование int в void free((void *) A); 4) Функция void *realloc(void*p, size_t new size) Изменяет размер ранее захваченного блока памяти, p – указатель на начало блока, size – размер в байтах. Блок может быть передвинут в памяти при изменении размера.
ДЕРЕВЬЯ. ОПРЕДЕЛЕНИЯ, КЛАССИФИКАЦИЯ, СПОСОБЫ ПРЕДСТАВЛЕНИЯ.
Дерево с базовым типом Т – это: 1) Либо пустое дерево 2) Либо вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т (поддеревья). (Дерево, на которое ссылается какая-либо вершина – поддерево)
Глубина(высота) = 3
Вершина, на которую непосредственно ссылается другая вершина – ее потомок. Обратная вершина – предок. Вершина, у которой нет потомков – лист дерева. Если пронумеруем вершины так, чтобы каждый следующий потомок был на уровень выше, то вершина, находящаяся на 0 уровне – корень дерева. Вершина, которая не является листом – внутренняя вершина. Уровень какой-либо вершины – глубина (высота), а глубина самого дерева - максимальная глубина из всех ее вершин. Количество непосредственных потомков вершины называется степенью данной вершины, степень дерева – максимальная из всех возможных степеней. Число ветвей (ребер), которые необходимо пройти от корня к вершине х, называется длиной пути к х (корень имеет путь 0). Длина пути всего дерева (длина внутреннего пути) – сумма длин путей до всех его вершин. Средняя длина пути определяется по формуле:
Упорядоченные деревья второй степени называются двоичными деревьями. Деревья n-ной (большей 2) степени называются сильно ветвящимися. Деревья, имеющие минимальную высоту, называются идеально сбалансированными (количество вершин в левом и правом поддереве отличаются не больше чем на 1 – условие для всех вершин).
Выражение таких рекурсивных структур требует использования ссылок. Существует множество различных способов представления деревьев (на примере бинарного дерева): 1) Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой – с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева. Можно заметить, что такой способ представления имеет сходство с простыми линейными списками. И это сходство не случайно. На самом деле рассмотренный способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков. Каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.
Tdata data;
struct binary_tree *right; } или struct TREE { Для обработки дерева достаточно знать адрес корневой вершины. Для хранения этого адреса надо ввести ссылочную переменную: Тогда пустое дерево просто определяется установкой переменной Root в нулевое значение:
2) В виде массива проще всего представляется полное бинарное дерево, так как оно всегда имеет строго определенное число вершин на каждом уровне. Вершины можно пронумеровать слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве.
Если число уровней дерева в процессе обработки не будет существенно изменяться, то такой способ представления полного бинарного дерева будет значительно более экономичным, чем любая списковая структура. Однако далеко не все бинарные деревья являются полными. Для неполных бинарных деревьев применяют следующий способ представления. Бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются. В массив заносятся только те вершины, которые были в исходном неполном дереве. При таком представлении элемент массива выделяется независимо от того, будет ли он содержать узел исходного дерева. Следовательно, необходимо отметить неиспользуемые элементы массива. Это можно сделать занесением специального значения в соответствующие элементы массива. В результате структура дерева переносится в одномерный массив. Адрес любой вершины в массиве вычисляется как: адрес Главным недостатком рассмотренного способа представления бинарного дерева является то, что структура данных является статической. Размер массива выбирается исходя из максимально возможного количества уровней бинарного дерева. Причем чем менее полным является дерево, тем менее рационально используется память.
ДВОИЧНЫЕ ДЕРЕВЬЯ, ОПЕРАЦИИ.
Двоичное дерево – конечное множество элементов (узлов), которое либо пусто, либо состоит из корня с двумя отдельными двоичными поддеревьями, которые называют левым и правым поддеревом корня. Для построения двоичного дерева с n вершинами, имеющего минимальную высоту, используются следующие правила: 0) Если n=0, то конец; 1) Построить вершину 2) Построить левое поддерево с 3) Построить правое поддерево с Операции с двоичными деревьями: 1) Обход дерева Учитывая рекурсивный характер правил обхода, программная их реализация наиболее просто может быть выполнена с помощью рекурсивных подпрограмм. Каждый рекурсивный вызов отвечает за обработку своего текущего поддерева. После полной обработки текущего поддерева происходит возврат к поддереву более высокого уровня, а для этого надо запоминать и в дальнейшем восстанавливать адрес корневой вершины этого поддерева. Рекурсивные вызовы позволяют выполнить это запоминание и восстановление автоматически, если описать адрес корневой вершины поддерева как формальный параметр рекурсивной подпрограммы.
· Префиксный обход – вершина, левое, правое (+ab):
{ if (t!=0) { print(t->data); //вершина prefix_walk(t->left); // левое prefix_walt(t->right); // правое } } · Инфиксный обход – левое, вершина, правое (a+b); · Постфиксный – левое, правое, вершина (ab+); 2) Поиск: При использовании в целях поиска элементов данных по значению уникального ключа применяются двоичные деревья поиска дерево поиска – все вершины в правом поддереве > x (вершина), все вершины в левом поддереве < x. N элементов можно организовать в бинарное дерево с высотой не более log2(N), поэтому для поиска среди N элементов может потребоваться не больше log2(N) сравнений, если дерево идеально сбалансировано. Отсюда следует, что дерево – это более подходящая структура для организации поиска, чем, например, линейный список.
Ищем 29:
3) Операция включения вершины в дерево: Операция включения элемента в дерево разбивается на три этапа: включение узла в пустое дерево, поиск корня для добавления нового узла, включение узла в левое или правое поддерево. Добавляем 50:
операции поиска, пока не дойдем до NULL.
4) Удаление вершины: Для удаления узла с указанным ключом сначала происходит его поиск. В случае, если узел найден, то он удаляется. · Если удаляемый узел не имеет потомков, то просто удаляется ссылка на него. · Если удаляемый узел имеет одного потомка, в этом случае переадресуется ссылка на этого потомка. · Если удаляемый узел имеет двух потомков, то на его место ставится самый правый потомок из левого поддерева или самый левый потомок из правого поддерева.
Удаляем 15 – ставим 14 или 16
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |

















 .
.

 Дерево называется упорядоченным, если все ветви, исходящие из любой вершины, также являются упорядоченными.
Дерево называется упорядоченным, если все ветви, исходящие из любой вершины, также являются упорядоченными.
 И - разные!
И - разные!



 struct bynary_tree{
struct bynary_tree{


 struct binary_tree *left;
struct binary_tree *left;

 , где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков: адрес_L
, где k-номер уровня вершины, i- номер на уровне k в полном бинарном дереве. Адрес корня будет равен единице. Для любой вершины можно вычислить адреса левого и правого потомков: адрес_L  и адрес_R
и адрес_R 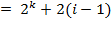
 вершинами;
вершинами; вершинами.
вершинами.


 Каждый рекурсивный вызов прежде всего должен проверить переданный ей адрес на NULL. Если этот адрес равен NULL, то очередное обрабатываемое поддерево является пустым и никакая его обработка не нужна, поэтому просто происходит возврат из рекурсивного вызова. В противном случае в соответствии с реализуемым правилом обхода производится либо обработка вершины, либо рекурсивный вызов для обработки левого или правого поддерева.
Каждый рекурсивный вызов прежде всего должен проверить переданный ей адрес на NULL. Если этот адрес равен NULL, то очередное обрабатываемое поддерево является пустым и никакая его обработка не нужна, поэтому просто происходит возврат из рекурсивного вызова. В противном случае в соответствии с реализуемым правилом обхода производится либо обработка вершины, либо рекурсивный вызов для обработки левого или правого поддерева. prefix_walk (struct binary_tree *t)
prefix_walk (struct binary_tree *t)


 Направляемся в корень, затем в L (<20)
Направляемся в корень, затем в L (<20)
 или R (>20) и т. д.
или R (>20) и т. д.



















 Ищем позицию аналогично
Ищем позицию аналогично






