
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое выделение памятиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Указатели позволяют создавать динамические массивы – массивы, память под которые выделяется на этапе выполнения программы. Напомним, что память под статические массивы выделяется при загрузке программы в память, до её выполнения и не может изменяться в процессе выполнения программы. Замечательно то, что размер динамических массивов может быть переменным, т. е. объём памяти выделяемой под массив, определяется во время выполнения программы. Доступ к элементам динамического массива происходит точно так же, как и к статическому массиву. Существуют два основных способа выделения динамической памяти под массивы:
а) с помощью операции new: int *uk1 = new int [100]; //1 б) с помощью функции malloc(): int *uk2 = (int *)malloc(400); //2
В случае а) операция new выделяет память под массив из 100 величин типа int и записывает адрес начала выделенного участка в переменную uk1, которая может трактоваться, как имя массива. Через это имя можно обращаться к любому элемента массива либо традиционно (через индексирование), либо с помощью операции разадресации; например, к четвертому элементу созданного массива можно обращаться как uk1[3] или *(uk1 + 3). В случае б) функции резервирования памяти malloc() передаётся один параметр – размер выделяемой памяти в байтах. Конструкция (int *) перед именем функции используется для явного преобразования типа указателя, возвращаемого функцией (он имеет тип void*), к требуемому типу. Функция возвращает указатель на начало выделенного участка, который присваивается переменной - указателю uk2. Если память выделить не удалось, то функция возвращает ноль. Память, выделенная под динамический массив с помощью операции new[], должна освобождаться оператором delete[], а память, зарезервированная функцией malloc() – с помощью функции free(), например:
delete [] uk1; free (uk2);
Следующая программа, используя собственную функцию revers(), позволяет обратить каждое слово в фразе, память под которую зарезервирована в динамической памяти с помощью функции malloc(). Слова в тексте разделяются произвольным количеством пробелов. Функция revers() реализована в двух вариантах: с указателями и с традиционной обработкой массива через индексирование.
// обратить в строке каждое слово void revers(char *s1);
int main()
{ char *s1; int Len;
// Устанавливаем локализацию для выходного потока wcout.imbue(locale("rus_rus.866")); // Выводим строку на русском! wcout<< L"Сколько байтов зарезервировать? "; cin >> Len; //scanf_s ("%d",&Len); fflush(stdin); // очистка буфера (или gets(s1);)
s1=(char*)malloc(Len); wcout << L"Введи строку "; gets(s1);
revers(s1); puts(s1); free(s1); getch(); return 0; }
// а) без указателей
void revers(char s1[]) { char r; int nw, kw, i=0; //nw, kw – номера символов
while(s1[i]) { //пропуск пробелов до слова while(s1[i]==' ') i++; nw=i;
//пропуск слова while(s1[i]!=' ' && s1[i]!='\0') i++; kw=i-1;
//переворот слова while(kw>nw) { r=s1[nw];s1[nw]=s1[kw]; s1[kw]=r;kw--;nw++; } } }
// б) с указателями
void revers(char *s1) { char r, *nw, *kw; //nw, kw – адреса символов
while(*s1) { //пропуск пробелов до слова while(*s1==' ') s1++; nw=s1;
//пропуск слова while(*s1!=' '&& *s1!='\0') s1++; kw=s1-1;
//переворот слова while(kw>nw) { r = *nw; *nw = *kw; *kw = r; kw--; nw++; } } }
Массивы указателей Указатели, подобно данным других типов, можно объединять в массивы. Вот, например, как выглядит определение массива из 5 указателей на int-значения. int *uka[5]; Здесь каждый элемент массива uka содержит указатель на целочисленное значение. Чтобы присвоить адрес int-переменной с именем x третьему элементу этого массива указателей, достаточно записать следующее. int x = 25; uka [2] = &x; Чтобы извлечь значение переменной x с помощью массива uka, используйте конструкцию вида: *uka [2] Поскольку адрес переменной x хранится в элементе uka[2], применение операции "*" к этой индексированной переменной и позволяет получить значение переменной x.
Наиболее часто массивы указателей используются для хранения указателей на строки. Рассмотрим пример использования массива символьных указателей для сортировки массива строк в алфавитном порядке.
Следующая программа реализует часто встречающуюся на практике задачу упорядочивания массива строк в алфавитном порядке. Обратите внимание, как реализована схема ввода массива строк. Функция ввода строки gets() помещена в заголовок цикла. Программа прекращает считывание строк с входного потока, когда встречается символ EOF (в этом случае функция gets() возвращает нуль), при нажатии Enter в начале вводимой строки (в этом случае функция gets() вводит пустую строку) или при достижении предела LIM. При нажатии клавиши Enter в начале ввода очередной строки в первый элемент строки помещается нуль-символ, поэтому выражение poem[i][0]!= ‘\0’ выполняет проверку на наличие пустой строки.
Кроме массива строк poem[i][0], в программе определён массив указателей на строки uks[], элементам которого последовательно в цикле присваиваются начальные адреса каждой строки. Для сортировки строк использован уже известный алгоритм «пузырька». Изюминка функции сортировки strsort() состоит в том, что вместо изменения порядка следования самих строк в функции был изменён лишь порядок следования указателей на строки. Порядок следования самих строк массива poem[][] остался неизменным. Основным инструментом в функции сортировки является функция strcmp(), позволяющая определить порядок следования двух строк.
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include<stdio.h> #include <string.h> #include <iostream> using namespace std;
const int LIM = 30, SIZE = 81;
int main() { void strsort(char *str[],int n); // прототип char poem[LIM][SIZE]; // "прямоугольный массив"
char *uks[LIM]; //МАСССИВ УКАЗАТЕЛЕЙ int k, i=0; // Устанавливаем локализацию для выходного потока wcout.imbue(locale("rus_rus.866")); // Выводим строку на русском! wcout<<L"Введи до "<<LIM<<L" строк для сортировки"<<'\n'; wcout<<L"Для прекращения - Enter в начале строки"<<'\n';
while((gets_s(poem[i])!= NULL)&& (poem[i][0]!='\0') && i<LIM)
{ uks[i]=poem[i]; //poem[i]- указатель на начало i-й строки! i++; }
//****************** strsort(uks,i); // i - реальное число введенных строк //******************
wcout<<L"Отсортированный куплет\n\n"; for(k=0;k<i;k++) puts(uks[k]); getch(); return 0; }
// сортировка строк методом "пузырька" void strsort(char *str[],int n) { char *ukr; int i,j; for(i=0; i<n-1; i++) for(j=i+1; j<n; j++) if(strcmp(str[i], str[j])>0) { ukr=str[i]; str[i]=str[j]; str[j]=ukr; } }
Для проверки программы мы ввели следующее четверостишие (из известных стихов об Одессе):
Чтоб это было да - так нет! Оно с Лузановкой поспорит? Гляди сюда и дай ответ: А взморья Рижского поклонник,
И вот результат:
Отсортированный куплет
А взморья Рижского поклонник, Гляди сюда и дай ответ: Оно с Лузановкой поспорит? Чтоб это было да - так нет!
В предыдущей программе каждая строка прямоугольного массива poem[LIM][SIZE] занимает в памяти ровно 81 байт. Модифицируем предыдущую программу, заменив в ней прямоугольный массив строк poem[LIM][SIZE] на так называемый ступенчатый (“рваный”) массив. Для этого определим массив указателей char *poem2[LIM] на значения типа char, и применим начальную инациализацию массива строк. При инициализации действуют обычные правила, применяемые для инициализации массивов. Следует только помнить, что в фигурных скобках первая пара двойных кавычек используется для инициализации указателя первой символьной строки; следующая пара двойных кавычек инициализирует второй указатель и т.д. Запятая разделяет соседние строки. Длина каждой строки такого массива определяется динамически и не имеет столь жёсткого ограничения – быть меньше длины SIZE. Этот ступенчатый массив не требует резервирования лишнего пространства в памяти.
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include<stdio.h> #include <string.h> #include <iostream> using namespace std;
const int LIM = 4;
int main() { void strsort(char *str[],int n); //"рваный массив" char *poem2[LIM] = { "Чтоб это было да - так нет!",
"Оно с Лузановкой поспорит?", "Гляди сюда и дай ответ:", "А взморья Рижского поклонник," };
//char *uks[LIM]; // ДОПОЛНИТЕЛЬНЫЙ МАСССИВ УКАЗАТЕЛЕЙ НЕ НУЖЕН
//****************** strsort(poem2,LIM); //******************
cout<<"Отсортированный куплет\n\n"; for(int k=0; k<LIM; k++) puts(poem2[k]); getch(); return 0; }
// сортировка строк методом "пузырька" void strsort(char *str[],int n) { char *ukr; int i,j; for(i=0; i<n-1; i++) for(j=i+1; j<n; j++) if(strcmp(str[i], str[j])>0) { ukr=str[i]; str[i]=str[j]; str[j]=ukr; } }
Остановимся на организации массива указателей чуть подробнее. Можно сказать, что массив poem2 – одномерный массив, состоящий из LIM элементов, и каждый элемент массива содержит адрес объекта типа char. Первый указатель – poem2[0] и он указывает на первый символ первой строки, второй указатель – poem2[1] и он ссылается на начало второй строки и т.д. Поэтому *poem2[0] = =’Ч’, *poem2[1] = =’О’, *poem2[2] = =’Г’ и т.д. В действительности массив poem2 не содержит никаких строк, он содержит лишь их адреса. А сами строки хранятся в теле кода основной программы. Из вышеизложенного ясно, почему в обновленной программе нам не понадобился дополнительный массив указателей uks[].
Функция типа указатель
Так говорят о функциях, явно возвращающих в качестве результата указатель на определенный тип данных. Указатели возвращаются подобно значениям любых других типов данных и не создают при этом особых проблем. Чтобы вернуть указатель, функция должна объявить его тип в качестве типа возвращаемого значения. Описание такой функции имеет вид:
тип *имя_функции (....)
Здесь <тип> есть тип данных, на которые ссылается возвращаемый функцией указатель. Например, описание известной библиотечной функции gets() имеет такой синтаксис:
char *gets(char *s)
Это функция типа “указатель на тип char”. Это означает, что после наполнения строки, соответствующей формальному параметру S, функция, кроме того, возвращает указатель на первый символ этой строки. Вот пример применения этой возможности.
#include<conio.h> #include <iostream> using namespace std;
int main() { char name[20]; cout << "Как тебя зовут? "; char *uks = gets(name); cout << "Привет, " << name << endl; cout << "Хорошее имя – " << uks << endl; return 0; }
Если функция возвращает указатель, то значение, используемое в ее инструкции return, также должно быть указателем. (Как и для всех функций, return-значение должно быть совместимым с типом возвращаемого значения.)
Замечание. Функция не может возвращать указатель на локальную переменную, поскольку память, выделенная под локальную переменную при активизации функции, освобождается по завершении работы функции.
Пример. int *fun(…) { int a=25; … return &a; // так нельзя! }
В следующей программе демонстрируется использование указателя в качестве типа возвращаемого значения. Функция substr() возвращает указатель на подстроку заданной длины L, выделенную из заданной строки S, начиная с заданной позиции K. Если номер K выходит за пределы исходной строки, то функция возвращает NULL-указатель. В теле функции используется вспомогательная строка my_str[], зарезервированная в динамической области памяти.
#include<conio.h> #include<stdio.h> #include <iostream> using namespace std;
char *substr(char *s, int k, int l); int main () { int k=5,l=5; char *bs="0123456789"; //char bs[40]="0123456789";
if(substr(bs,k,l)==NULL) puts("нет подстроки"); else puts(substr(bs,k,l)); puts("Исходная строка"); puts(bs); getch();return 0; }
//функция типа указатель выделяет подстроку
char *substr(char *s, int k, int l) { if(k<0 || k>strlen(s)) return NULL;
char *my_str= new char [strlen(s)]; //char *my_str=(char*)malloc(strlen(s)); strcpy(my_str,s); if(k +l < strlen(s)) *(my_str + k + l)='\0'; return(my_str + k); }
Разберитесь самостоятельно, как работает следующая программа с функцией копирования строки.
// copy.cpp строки #include <string.h> #include <stdio.h> #include <conio.h>
char *copy(char *s1, char *s2) { char *uk1=s1; while((*s1++ = *s2++)!= '\0') ; return uk1; } int main() { char s1[80], s2[40]; clrscr(); printf("введи cтроку\n"); gets(s2); puts(copy(s1, s2)); getch(); return 0; }
Указатель на функцию
Указатель на функцию содержит адрес в сегменте кода, по которому располагается исполняемый код функции, то есть адрес, по которому передается управление при вызове функции. Указатели на функции используются для косвенного вызова функции (не через ее имя, а через обращение к переменной, хранящей ее адрес), а также для передачи имени функции в другую функцию в качестве параметра. Указатель функции имеет тип «указатель функции, возвращающей значение заданного типа и имеющей аргументы заданного типа»:
тип (*имя) (список_типов_аргументов);
При объявлении указателя функции необходимо описать её тип. Для обозначения типа функции указывается её возвращаемый тип, а также типы параметров. Рассмотрим следующий прототип: int my_fun (double, double); Функция my_fun возвращает значение типа int и имеет два параметра типа double. Чтобы объявить указатель pf на данный тип функции, вводится следующее описание:
int (*pf) (double, double);
Из этого объявления видно, что первая пара скобок связывает операцию * с pf. Это означает, что pf является указателем на функцию. Таким образом, (*pf) является функцией со списком параметров (double, double) и возвращаемым типом int. Итак, чтобы объявить указатель на определенный тип функции, нужно сначала объявить функцию желаемого типа, а затем заменить имя функции выражением в форме (*pf); при этом pf становится указателемнафункцию данного типа. Полученному указателю функции можно присваивать адреса функций соответствующего типа, например, pf=my_fun; Напомним, что в программе на С/C++ адресом функции служит ее имя без скобок и аргументов (это похоже на адрес массива, который равен имени массива без индексов).
Пусть имеется описание double a=17.5, b=21.3; Тогда выражения(* pf)(a, b) и my_fun(a, b) эквивалентны. Указатель на функцию чаще всего применяется для передачи её имени как аргумента в другую функцию. Рассмотрим следующую программу, в которой сравниваются две строки, введенные пользователем. Обратите внимание на объявление функции check() и указателя fp внутри main(). Указатель fp, как вы увидите, является указателем на функцию. #include "stdafx.h" #include <stdio.h> #include <string.h> #include<iostream> using namespace std;
void check(char *a, char *b, int (*cmp)(const char *, const char *));
int main(void) { char s1[80], s2[80]; system("chcp 1251"); int (*fp)(const char *,const char *); // указатель на функцию
fp = strcmp; // присваивает адрес функции strcmp указателю fp
printf("Введите две строки.\n"); gets(s1); gets(s2);
check(s1, s2, fp); // Передает адрес функции strcmp посредством указателя fp
return 0; }
void check(char *a, char *b, int (*cmp)(const char *, const char *)) { printf("Проверка на совпадение.\n"); if(!(*cmp)(a, b)) printf("Равны"); else printf("Не равны"); }
Проанализируем эту программу подробно. В первую очередь рассмотрим объявление указателя fp в main():
int (*fp)(const char *, const char *);
Это объявление сообщает компилятору, что fp — это указатель на функцию, имеющую два параметра типа const char * и возвращающую значение типа int. Скобки вокруг fp необходимы для правильной интерпретации объявления компилятором. Подобная форма объявления используется также для указателей на любые другие функции, нужно лишь внести изменения в зависимости от возвращаемого типа и параметров функции.
Теперь рассмотрим функцию check(). В ней объявлены три параметра: два указателя на символьный тип (a и b) и указатель на функцию cmp. Обратите внимание на то, что указатель функции cmp объявлен в том же формате, что и fp. Поэтому в cmp можно хранить значение указателя на функцию, имеющую два параметра типа const char * и возвращающую значение int. Как и в объявлении fp, круглые скобки вокруг *cmp необходимы для правильной интерпретации этого объявления компилятором.
Вначале в программе указателю fp присваивается адрес стандартной библиотечной функции strcmp(), которая сравнивает строки. Потом программа просит пользователя ввести две строки и передает указатели на них функции check(), которая их сравнивает. Внутри check() выражение (*cmp)(a, b) вызывает функцию strcmp(), на которую указывает cmp, с аргументами a и b. Скобки вокруг *cmp обязательны. Существует и другой, более простой, способ вызова функции с помощью указателя: cmp(a, b); Однако первый способ используется чаще, потому что при втором способе вызова указатель cmp очень похож на имя функции, что может сбить с толку читающего программу. В то же время у первого способа записи есть свои преимущества, например, хорошо видно, что функция вызывается с помощью указателя на функцию, а не имени функции. Вызов функции check() можно записать, используя непосредственно имя strcmp(): check(s1, s2, strcmp); В этом случае вводить в программу дополнительный указатель fp нет необходимости.
Может возникнуть вопрос: какая польза от вызова функции с помощью указателя на функцию? Ведь в данном случае никаких преимуществ не достигнуто, этим мы только усложнили программу. Тем не менее, во многих случаях оказывается более выгодным передать имя функции как параметр. В частности, использование указателей на функции позволяет в разные моменты осуществлять передачу функции адресов различных функций.
Покажем это на конкретных примерах.
Пример 1. Приближенное вычисление корней уравнений. ПОСТАНОВКА ЗАДАЧИ Создать набор функций для вычисления с точностью ε =10-5 значения корня x* уравнения F(x)=0 на интервале [a, b] методом деления отрезка пополам (методом дихотомии). Имя конкретной функции F(x) передать вызываемой подпрограмме как параметр. Полагается, что F(a)*F(b)<0, т.е. корень находится на отрезке [a, b].
Рассмотреть варианты: 1) F(x)= x-Sinx-0.25 a=1, b=2 корень=1.171229
2) F(x)= x*x-5*x+6 a=2.5, b=3.3 корень=3
3) F(x)= 2*x-Cos(x) a=0, b=1 корень=0.450184
АЛГОРИТМ РЕАЛИЗАЦИИ ПОСТАВЛЕННОЙ ЗАДАЧИ
Ищутся корни уравнения F(x)=0, в предположении, что функция F(x) является непрерывно дифференцируемой на промежутке [a, b]. Будем считать, что корни уравнения (1) отделены и один из них лежит на промежутке [a, b] Алгоритм метода деления отрезка пополам нахождения корней уравнения (1) состоит в следующем. Отрезок [a, b] точкой Отрезок [a1,b1] точкой На n-ом шаге получим отрезок [an, bn], на концах которого функция F(x) принимает значения противоположных знаков. При этом корень x* уравнения (1) принадлежит промежутку [an, bn]. Процесс завершается, если | bn –an | ≤ Тогда в качестве приближенного значения xn корня x* уравнения (1) можно взять xn=an либо xn=bn..
ОПИСАНИЕ ИСПОЛЬЗУЕМЫХ ФУНКЦИЙ
В состав программного комплекса входят следующие подпрограммы. 1) ZERO – функция, реализующая вычисление с точностью ε =10-5 значения корня x* уравнения F(x)=0 на интервале [a, b] методом деления отрезка пополам (методом дихотомии). Вот алгоритм кратко. 1. Находим c = (a + b )/2 2. Вычисляем F(c). 3. Если F(c)=0, считаем, что x* = c и заканчиваем вычисления. 4. Если F(c)* F(a)> 0, задаём a = c, иначе b = c. 5. Проверяем условие | b – a | >ε; если оно выполняется, идём к п.1, иначе – заканчиваем вычисление, считая, что x* = c
Заголовок функции
double zero(double a,double b,double eps,double (*uf)(double))
содержит формальный параметр (*uf)(double)) – указатель на функцию F(x). Реальное имя функции, соответствующее этому формальному параметру, передается функции zero при её вызове, например:
x=zero(a,b,eps,FSin);
2) Программная функция F(x) предназначена для вычисления значений тестируемой функции. Программа содержит несколько таких функций, согласно вариантам исходного задания и варианты для тестирования (с очевидными ответами). Заголовок функции очевиден: double f1(double x)
3) В основной программе осуществляется ввод исходных данных – интервала отделения корня [ a, b ] и номера тестируемой функции num_F, согласно которому процедура zero вызывает конкретную функцию для уточнения корня. Последнее реализуется оператором switch (num_F). Программа использует глобальную переменную FLAG логического типа, по состоянию которой можно судить об удачном или аварийном завершении процедуры zero. Состояние FLAG=false возникает, если не выполнено условие F(a)*F(b)<0 (т.е.,возможно, корни не отделены).
//zero_2013.cpp апрель 2013г. //Вычисление корня уравнения F(x)=0 методом половинного деления // В заголовке функции ZERO используется формальный параметр- // указатель на функцию (*uf). При вызове этой функции в каче- // стве фактического параметра ей передается имя реальной // функции: F1, F2, F3,...
#include "stdafx.h" #include <conio.h> # include <math.h> #include <iostream> using namespace std;
//Прототипы используемых функций double f1(double x); double f2(double x);double f3(double x); double zero(double,double,double,double (*uf)(double));
bool FLAG; // ФЛАГ УДАЧИ - глобальная переменная
int main() { system("chcp 1251"); system("cls"); double a, b; // интервал локализации корня double eps; // точность вычисления корня int num_F; // номер функции: 1,2,3 double x; // корень уравнения F(x)=0
eps=1e-5; FLAG=false;
//********************************* m2: cout<<"ВВЕДИ номер вызываемой функции: 1,2,3"; cin>>num_F; if (num_F < 1 || num_F > 3) {cout<<"ERROR num_F "; goto m2;}
cout<<"ВВЕДИ A "; cin>>a; cout<<"ВВЕДИ B "; cin>>b;
//**********ВЫЗОВ ФУНКЦИИ ZERO*************
switch (num_F) { case 1: x=zero(a,b,eps,f1); break; // для функции F1 case 2: x=zero(a,b,eps,f2); break; // для функции F2 case 3: x=zero(a,b,eps,f3); break; // для функции F3 } /**************************************/
if(FLAG==true) cout<<"Корень равен "<<x<<endl; else { cout<<"Не могу найти корень"<<endl; cout<<"не выполнено условие F(a)*F(b)<0"<<endl; cout<<"(т.е, возможно, корни не отделены)"<<endl;
}
_getch(); return 0; }
// 1 тестируемая функция double f1(double x) { return x-sin(x)-0.25; // a=1, b=2 корень=1.171229 }
// 2 тестируемая функция
double f2(double x) { return x*x-5*x+6; // корни: 2 и 3 }
// 3 тестируемая функция
double f3(double x) { return 2*x-cos(x); // a=0, b=1 корень=0.450184 }
// Эта функция реализует метод дихотомии (метод половинного // деления интервала [a, b]) для вычисления с точностью eps // значения корня x* уравнения F(x)=0 на интервале [a, b]
double zero(double a,double b,double eps,double (*uf)(double)) {
double c; FLAG=true; if((*uf)(a)*(*uf)(b)>0) { FLAG=false; //НЕ ВЫПОЛНЕНО УСЛОВИЕ F(a)*F(b) < 0 КОРЕНЬ НЕ НАЙДЕН return 0; }
while (fabs(b-a)>eps) { c=(a+b)/2; if ((*uf)(c)==0) return(c); if ((*uf)(a)*(*uf)(c)<=0) b=c; else a=c; } return (a+b)/2; }
Пример 2. Приближенное вычисление определенных интегралов.
ПОСТАНОВКА ЗАДАЧИ Составить программу для вычисления с заданной точностью ε =10-5 определённого интеграла
используя метод трапеций. Для реализации метода и вычисления f(x) использовать подходящие функции. Имя функции f(x) передать вызываемой подпрограмме как параметр.
Формула трапеций:
где fi = f(xi), xi = a + ih, h = (b - a)/n
Для достижения требуемой точности при вычислении интеграла по квадратурной формуле использовать метод последовательного удвоения числа шагов.
Рассмотреть варианты: 1 )f(x) = a = 0, b = 1 Ответ: 1.398717 2) f(x) = x2 a = 0, b = 1 Ответ: 0.33333
3) f(x) = sin(x/4) a = 0, b = 1 Ответ: 0.124344 1. О приближенном вычислении определенных интегралов Задачи вычисления определенных интегралов
Но во многих случаях первообразную F(x) функции f(x) в элементарных функциях найти невозможно или она получается слишком сложной. В таких случаях применяются различные методы приближенного вычисления определенных интегралов: метод прямоугольников, метод трапеций, метод парабол (метод Симпсона) и др.
Для этого промежуток [a, b] разбиваем точками
на частичные промежутки Точки
Отметим геометрический смысл определенного интеграла. Если Если же функция
В связи с этим обстоятельством при выводе квадратурных формул приближенного вычисления определенных интегралов будем предполагать, что функция
Описание метода трапеций Этот метод основан на том, что площадь криволинейной фигуры, ограниченной кривой y=f(x) и прямыми x=xi, x=xi+1 и y=0, то есть интеграл
то есть Тогда квадратурную формулу трапеций приближенного вычисления определенного интеграла I можно записать в виде
Для достижения требуемой точности при вычислении по квадратурной формуле используется метод последовательного удвоения числа шагов. Для вычисления значения интеграла с заданной степенью точности необходимо первоначально принять некоторое произвольное количество разбиений участка интегрирования, например, n = 10 и вести расчет интеграла сначала при этом количестве разбиений, а затем при удвоенном, т.е. n = 20, затем при n = 40 и т.д. до тех пор, пока погрешность не станет меньше или равной заданной точности.
ПРОГРАММНЫЙ КОМПЛЕКС
// integral.cpp Приближенное вычисление определенного // интеграла методом трапеций // Для достижения требуемой точности при вычислении по // квадратурной формуле используется метод последовательного // удвоения числа шагов n участка интегрирования.
#include "stdafx.h" #include <conio.h> #include <stdio.h> #include <iostream> using namespace std;
// вычисление 1 подынтегральной функции double Fsqrt(double x) { return sqrt(2*x+1); // a = 0, b = 1 Ответ: 1.398717
}
// вычисление 2 подынтегральной функции double Fsin(double x) { return sin(x/4); //a = 0, b = 1 Ответ: 0.124344 }
// вычисление 3 подынтегральной функции double Fsqr (double x) { return x*x; //a = 0, b = 1 Ответ: 0.3333
}
// вычисление 4 подынтегральной функции double f (double x) { return log(x); //a = 1, b = 2 Ответ: }
// Функция вычисления интеграла методом трапеций // В заголовке функции TRAP используется формальный параметр-указатель // на функцию (*uf). При вызове этой функции в качестве фактического // параметра ей передается имя реальной функции: Fsqrt, Fsin, Fsqr // через оператор switch (num_F)
double trap(double a, double b, int n,double (*uf)(double)) { int i; double h,s; h=(b-a)/n; s=((*uf)(a)+(*uf)(b))/2; for(i=1; i<= n-1; i++) s=s+(*uf)(a+i*h); s=s*h; return s; }
// основная программа int main() { system("cls"); system("chcp 1251"); double a, b; // интервал интегрирования double eps; // точность вычисления интеграла double s1,s2; // последовательные приближения к интегралу int n; // число интервалов интегрирования int num_F; // номер функции: 1,2,3
eps=0.00001; n=10;
//******************************************* m2: cout<<"ВВЕДИ номер вызываемой функции: 1,2,3"; cin>>num_F; if (num_F < 1 || num_F > 3) {cout<<"ERROR num_F "; goto m2;}
cout<<"ВВЕДИ A "; cin>>a; cout<<"ВВЕДИ B "; cin>>b;
//**********ВЫЗОВ ФУНКЦИИ TRAP************* switch (num_F) { case 1: s1=trap(a,b,n,Fsqrt); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s1); do { n=n*2; s2=trap(a,b,n,Fsqrt); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s2); if(fabs(s2-s1)<eps) break; s1=s2; } while(1); break; // для функции F1
case 2: s1=trap(a,b,n,Fsin); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s1); do { n=n*2; s2=trap(a,b,n,Fsin); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s2); if(fabs(s2-s1)<eps) break; s1=s2; } while(1); break; // для функции F2
case 3: s1=trap(a,b,n,Fsqr); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s1); do { n=n*2; s2=trap(a,b,n,Fsqr); //вызов функции-метода printf("n = %5d интеграл =%10.6lf\n", n, s2); if(fabs(s2-s1)<eps) break; s1=s2; } while(1); break; // для функции F3 } return 0; }
Далее следуют примеры программ, использующих функции и указатели.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.86.70 (0.018 с.) |

 (1)
(1) [a, b]. При этом выполняется условие F(a)×F(b)<0, т.е. функция F(x) на концах промежутка [a, b] имеет значения противоположных знаков.
[a, b]. При этом выполняется условие F(a)×F(b)<0, т.е. функция F(x) на концах промежутка [a, b] имеет значения противоположных знаков. делим на два отрезка
делим на два отрезка  ,
,  . Если
. Если  , то корень уравнения (1) найден, т.е.
, то корень уравнения (1) найден, т.е.  . Если же
. Если же  , то обозначим через [a1,b1] тот из отрезков
, то обозначим через [a1,b1] тот из отрезков 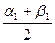 снова делим на два отрезка
снова делим на два отрезка  ,
, 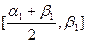 . Если
. Если  , то корень уравнения (1) найден, т.е.
, то корень уравнения (1) найден, т.е.  . Если же
. Если же 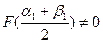 , то обозначим через [a2, b2] тот из отрезков
, то обозначим через [a2, b2] тот из отрезков  ,
, ≈ h[ (f0 +fn )/2+f1+ … + fn-1],
≈ h[ (f0 +fn )/2+f1+ … + fn-1],
 возникают во многих областях прикладной математики и инженерных расчетах. Если известна первообразная F(x) функции f(x), т.е. F' (x)= f(x), то вычисление определенного интеграла производится по формуле Ньютона-Лейбница
возникают во многих областях прикладной математики и инженерных расчетах. Если известна первообразная F(x) функции f(x), т.е. F' (x)= f(x), то вычисление определенного интеграла производится по формуле Ньютона-Лейбница
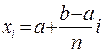 ,
, 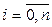 ,
,  ,
,  (1)
(1)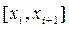 ,
,  ,
,  .
.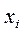 называются узлами квадратурной формулы, промежутки
называются узлами квадратурной формулы, промежутки  называются частичными промежутками интегрирования, а величина
называются частичными промежутками интегрирования, а величина  называется шагом интегрирования. При этом интеграл можно представить в виде
называется шагом интегрирования. При этом интеграл можно представить в виде (2)
(2) на промежутке [a, b], то определенный интеграл I представляет собой площадь S криволинейной трапеции (фигуры), ограниченной кривой y=f(x) и прямыми x=a, x=b и y=0, то есть I=S.
на промежутке [a, b], то определенный интеграл I представляет собой площадь S криволинейной трапеции (фигуры), ограниченной кривой y=f(x) и прямыми x=a, x=b и y=0, то есть I=S. отрицательна или меняет знак на промежутке [a, b], то площадь S криволинейной трапеции (фигуры), ограниченной кривой y=f(x) и прямыми x=a, x=b и y=0, равна
отрицательна или меняет знак на промежутке [a, b], то площадь S криволинейной трапеции (фигуры), ограниченной кривой y=f(x) и прямыми x=a, x=b и y=0, равна
 и непрерывна на промежутке [a, b]. Однако полученные квадратурные формулы будут справедливы и для любой непрерывной функции.
и непрерывна на промежутке [a, b]. Однако полученные квадратурные формулы будут справедливы и для любой непрерывной функции.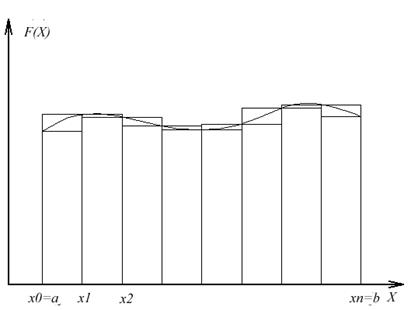
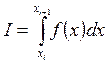 , заменяется площадью прямоугольной трапеции с основаниями
, заменяется площадью прямоугольной трапеции с основаниями 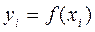 ,
,  и высотой
и высотой 






