
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Программирование алгоритмов с использованием функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функции по сути являются строительными блоками, с помощью которых в С/С++ создаются программные проекты. Функция представляет логически завершенную часть программного кода, которая может быть независимо откомпилирована, протестирована и вызвана на выполнение. Функция может иметь формальные параметры, которые при её вызове заменяются на фактические параметры (аргументы). Определение функции состоит из двух частей: заголовка и тела. Заголовок определяет имя функции, ее тип и формальные параметры. Тело функции — это составной оператор (блок), содержащий описания и операторы, реализующие алгоритм работы функции. Другими словами, тело функции определяет действия над данными, выполняемые функцией. Синтаксис определения функции: [inline][класс памяти] тип имя ([описание формальных параметров/void]) { описания; операторы; [return [ <выражение>]; ] } Здесь квадратные скобки указывают, что заключенная в них конструкция может отсутствовать. Описатель inline означает, что код функции при каждом ее вызове встраивается (“монтируется ”) в тело вызывающей программы (в точку вызова). Это должно увеличить быстродействие программы. В определении функции допускается указание класса памяти static или extern (см. раздел “Описание переменных”). Область действия функции, объявленной со спецификацией класса памяти extern, распространяется на все модули программы, т.е. она может быть вызвана из любой точки любого файла программного проекта (принимается по умолчанию). Если же использован описатель static, то область действия такой функции – только в пределах того файла, в котором она определена. Описатель тип определяет тип возвращаемого функцией значения. Им может быть любой тип, кроме массива и функции. Возвращаемое функцией значение передается в вызывающую программу оператором return < выражение >. Значение <выражения> и есть результат работы функции. Оно вычисляется, преобразуется к типу возвращаемого значения и возвращается в точку вызова функции. (Тип возвращаемого значения должен быть совместимым с типом данных, используемых в операторе return). Функция может ничего не возвращать в точку вызова. В этом случае её тип должен быть void, а оператор return, размещённый в конце функции, быть пустым, либо он вообще отсутствует. Таким образом, функция завершается и управление передается вызывающей программе при достижении закрывающей фигурной скобки или оператора return.
При описании формальных параметров следует иметь в виду, что каждый из них должен иметь индивидуальный описатель типа, а элементы списка разделяются запятыми, например: double Geron(double x, double y, double z) Формальные параметры функции полностью локализованы в ней и недоступны вне функции. Для активизации функции осуществляют её вызов. Чтобы вызвать функцию, достаточно указать ее имя с парой круглых скобок, в которых функции передаётся список фактических параметров (аргументов). Аргументы должны соответствовать формальным параметрам по типу, количеству и порядку их следования; совпадение имён тех и других не имеет значения. Фактические параметры передаются функции по значению (это не относится к массивам и строкам). Это означает, что значение (быть может, предварительно вычисленное) каждого фактического параметра заменяет при вызове функции соответствующий формальный параметр и действия, предусмотренные алгоритмом функции, осуществляется именно над этими значениями. Понятие о прототипе функции. Будем различать определение функции и ее объявление. Определение, как уже упоминалось, содержит заголовок и тело функции, представляющее собой последовательность операторов и описаний данных в фигурных скобках. Не требуется, чтобы определение функции обязательно предшествовало вызову функции. Определения используемых функций могут следовать за определением функции main() или могут находиться вообще в другом файле. Однако для того, чтобы компилятор мог выполнить проверку соответствия типов передаваемых аргументов типам формальных параметров в определении функции, до вызова функции нужно поместить её предварительное объявление (прототип). Прототип функции имеет такой же формат, что и заголовок функции, с той лишь разницей, что он заканчивается точкой с запятой, например: double Geron(double, double, double); Прототип функции задаёт её имя, типы и число формальных параметров, тип значения, возвращаемого функцией, и, быть может, класс памяти (мы этим атрибутом пользоваться пока не будем). Формальные параметры могут иметь имена, но компилятор их игнорирует.
Компилятор использует прототип функции для согласования типов фактических параметров при вызове функции с типами формальных параметров, и для контроля типа возвращаемого функцией значения. Как уже упоминалось, функция возвращает значение, если при её выполнении достигнут оператор return вида return <выражение>; < Выражение > вычисляется, преобразуется, если необходимо, к типу возвращаемого значения, указанному в определении (объявлении) функции, и управление возвращается в точку вызова. Если функция не возвращает результат в точку вызова, то вызов имеет вид самостоятельного оператора, например: Sleep(time); В противном случае имя функции со списком фактических параметров используется как составная часть некоторого выражения, например S = Geron(a,b,f) + Geron(c,d,f); Список формальных параметров функции и соответственно список аргументов функции при её вызове может отсутствовать, но скобки сохраняются, например: clrscr(); При завершении функции значения формальных параметров и значения локальных переменных функции, полученные ими в процессе работы функции, теряются (если только при её определении не был указан класс памяти static).
Замечание. Вызовы функций могут осуществляться по-разному, в зависимости от наших потребностей. Например, известная функция ввода данных scanf(“%d %d”, &a, &b); согласно её синтаксису может быть вызвана так: int k= scanf(“%d %d”, &a, &b); Здесь k – количество правильно прочитанных переменных.
Площадь треугольника с известными длинами сторон x, y, z вычислим, используя формулу Герона: S =, где p = (x + y + z)/2.
Соответствующая программа с функцией Geron() может иметь показанный ниже вид:
#include <conio.h> #include <iostream.h> #include <math.h> double Geron(double, double, double); // прототип void main() { double a,b,c,d,f; clrscr(); cout<<"Введи стороны четырехугольника "; cin>>a>>b>>c>>d; cout<<"Введи диагональ четырехугольника "; cin>>f; cout<<"Его площадь="<<Geron(a,b,f)+Geron(c,d,f); getch(); } // Функция «формула Герона»:
double Geron(double x, double y, double z) { double p=(x+y+z)/2; return sqrt(p*(p-x)*(p-y)*(p-z)); }
Задача 53. Программа использует функцию NOD() для нахождения наибольшего общего делителя двух заданных натуральных чисел A и B. Найденное значение использеется для вычисления наименьшего общего кратного (NOK) этих чисел.
// Напомним, что NOK(a,b)= a*b/NOD(a,b) // Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include <iostream> using namespace std;
// Функция вычисления наибольшего общего делителя unsigned NOD(unsigned a, unsigned b) { unsigned r; //if(a < b){r = a; a = b; b=r;} while (a % b) { r = a % b; a = b; b = r; } return b; } // Основная: int main() { unsigned a, b, nod; // Устанавливаем локализацию для выходного потока wcout.imbue(locale("rus_rus.866")); // Выводим строку на русском! wcout<<L"Введи 2 натуральных числа "; cin>>a>>b; nod=NOD(a, b); wcout<<L" Наибольший общий делитель = "<<nod<<endl;
wcout<<L" Наименьшее общее кратное = "<<a*b/nod<<endl; getch(); return 0; }
Задача 54. Программа делает безуспешную попытку с помощью функции noswap() обменять местами значения двух переменных. Программа иллюстрирует тот факт, что параметры — простые переменные (но не массивы и строки!) передаются функции по значению. Это означает, что любое изменение таких формальных параметров в теле функции никоим образом не влияет на значения соответствующих фактических параметров в вызывающей программе.
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include <iostream> using namespace std;
// Т.к. функция текстуально расположена в файле после // точки её вызова, то до вызова функции необходимо // привести её прототип void noswap (int a, int b); //указывается прототип функции
int main() { int a =5, b = 7; cout <<"a="<<a<<" b="<<b<<endl; noswap (a, b); cout <<"a="<<a<<" b="<<b<<endl; getch(); return 0; }
void noswap (int a, int b) { int rab = a; a = b; b = rab; cout <<"a="<<a<<" b="<<b<<endl; }
Задача 55. Программа находит в заданном диапазоне натуральных чисел [A, B] все числа–“перевертыши”. Решающую роль в поиске играет функция revers(), которая заданное натуральное число N преобразует в натуральное число M, представленное теми же цифрами, что и N, но взятыми в обратном порядке.
// Программа отлажена в Visual Studio 2008 (8.04.2008) #include "stdafx.h" #include <conio.h> #include <iostream> using namespace std;
unsigned long revers (unsigned long n) { int z; unsigned long m = 0; while(n!=0) { z = n%10; m = m*10 + z; n = n/10; } return m; }
int main() { unsigned long A, B, n, m; // Устанавливаем локализацию для выходного потока wcout.imbue(locale("rus_rus.866")); // Выводим строку на русском языке! wcout<<L"Введи начало диапазона "; cin>>A; wcout<<L"Введи конец диапазона "; cin>>B;
wcout<<L"\n Вот числа-перевертыши:\n"; for (n=A; n<B; n++) { m = revers(n); if (m==n) cout <<n<<endl; } getch(); return 0; }
Задача 56. Программа с помощью собственной функции letter() преобразует каждую введенную прописную латинскую букву в строчную и наоборот. Другие введенные символы функия letter() оставляет без изменения. Замечание. Для преобразования букв латинского алфавита в верхний и нижний регистры можно использовать библиотечные функции toupper() и tolover() соответственно. // Программа отлажена в Visual Studio 2008 (3.05.2008) #include "stdafx.h" #include <stdio.h> #include <iostream> #include <conio.h> using namespace std;
// bukva.c функция преобразования букв char letter(char symbol) { if (symbol>='A' && symbol<='Z') return(symbol | 0x20); // c1=c+32 else if (symbol >= 'a' && symbol <= 'z')
return(symbol & 0xDF); // c1=c-32 else return(symbol); // нет преобразования }
int main() { char ch; printf("введи букву\n"); scanf("%c",&ch); printf("%c-%c",ch,letter(ch)); getch(); return 0; }
Задача 57. Программа находит максимум из 5-ти чисел.
// Программа отлажена в Borland C++ Builder 6 #include <iostream.h> #include <conio.h> // Функция нахождения максимума из 2-х чисел: float max(float x, float y) { if (x>y) return x; Else return y; } // Основная: int main() { clrscr(); float a, b, c, d, f; gotoxy(25, 10); cout<<"Введи 5 чисел \n"; cin>>a>>b>>c>>d>>f; gotoxy(25, 12); cout<<"Max = "<< max(a,max(b,max(c,max(d,f)))); getch();return 0;
}
Задача 58. Программа использует собственную функцию what_chr(), чтобы распознать, какая из клавиш была нажата и сообщить ее код ASCII. Обратите внимание, что коды клавиш управления курсором, в отличие от обычных клавиш, занимают в памяти не один, а два байта, первый из которых — нулевой или имеющий код 0xE0.
// Программа отлажена в Borland C++ Builder 6 #include "d:\\My_C_Builder_6\\rus.h" #include <stdio.h> #include <conio.h> //Функция распознает код нажатой клавиши void what_chr(int ch) { if (ch == 0 || ch == 0xE0) { ch=getch();printf(rus("Спецклавиша - Расширенный скэн-код %u "),ch); switch (ch) { case 72: printf(rus("Стрелка вверх \n")); break; case 80: printf(rus("Стрелка вниз \n")); break; case 75: printf(rus("Стрелка влево \n")); break; case 77: printf(rus("Стрелка вправо\n")); break; case 71: printf(rus("Клавиша Home \n")); break; case 79: printf(rus("Клавиша End \n")); break; default: printf(rus("Остальные клавиши - сам...сам...\n")); } } Else printf(rus("Обычная клавиша %c"\ "(Код %u)\n"),ch,ch); }
void main() { int ch; clrscr(); do { puts(rus("\nВведи символ или ESC")); what_chr(ch=getch()); } while (ch!= 27); }
Задача 59. Программа изображает равнобедренный треугольник заданной высоты, заполненный символом ‘*’. Для построения фигуры использована функция piramida(). Для позиционирования курсора в заданную позицию строки экрана использован переменный формат, поддерживаемый функцией printf().
// Программа отлажена в Visual Studio 2008 (3.05.2008) #include<conio.h> #include<stdio.h> #include <iostream> using namespace std; // Функция построения треугольника:
void piramida(int h) { int k, i; for(k=0; k<=h; k++) { printf("%*c", 40-k, ' '); //переменный формат for(i=40-k; i<=40+k; i++) cout<<"*"; cout<<"\n"; } } // Основная: int main() { int h; cout<<"Vvedi visoty "; cin>>h; piramida(h); getch();return 0; }
Задача 60. Программа изображает равнобедренный треугольник заданной высоты, заполненный символом ‘*’. Вершина треугольника располагается в 40 колонке экрана. Для вывода на экран заданного символа заданное число раз использована функция put_ch().
// Программа отлажена в Visual Studio 2008 (3.05.2008) #include<conio.h> #include<stdio.h> #include <iostream> using namespace std;
void put_ch(int m,char ch) { while(m>0) { putchar(ch); m--; } }
int main() { int y, i=0; char x = '*'; cout <<" vvedi visotu"; cin >>y; while(i<y) { put_ch(39-i,' '); // pechat 39-i probelov put_ch(2*i+1, x); // pechat 2*i+1 simvolov i++; cout<<'\n'; } getch(); return 0; }
Задача 61. Программа изображает равнобедренный треугольник (пустотелый) заданной высоты. Стороны треугольника нарисованы символом с кодом ASCII 002. Вершина треугольника располагается в 40 колонке экрана. Решающую роль в построении играет функция put_ch(), выводящая на экран заданный символ заданное число раз.
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include <iostream> #include <conio.h> using namespace std;
// Функция, выводящая на экран заданный // символ заданное число раз
void put_ch(char c,int n) { while(n--) putchar(c); }
int main() { int i=0,n; // Устанавливаем локализацию для выходного потока wcout.imbue(locale("rus_rus.866")); // Выводим строку на русском! wcout<< L"Введи высоту треугольника "; cin>>n;
for(int k=0; k < 40; k++) putchar(' '); putchar('\002');putchar('\n'); while(i<=n) { put_ch(' ',39-i); putchar('\002'); put_ch(' ',2*i+1); putchar('\002'); putchar('\n'); i++; } put_ch(' ',39-i); put_ch('\002',2*n+5); getch(); return 0; }
Задача 62. В следующей программе функция byte() преобразует заданное целое число в его двоичный эквивалент. В вызывающей программе тестируемые числа вводятся последовательно до тех пор, пока не будет введен какой-нибудь нечисловой символ, который распознает функция ввода scanf(). (Напомним, что эта функция возвращает в качестве результата количество реально введенных данных).
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include<stdio.h> #include <iostream> using namespace std;
void byte(int n) { int i; for(i=8*sizeof(int)-1; i>=0; i--) putchar(n&(1<<i)? '1': '0'); }
int main() { int num;
printf("Введи число или Q "); while (scanf("%d",&num)==1) { printf("%d будет ", num); byte (num); printf("\nВведи число или Q "); } return 0; }
Задача 63. Треугольник задан координатами своих вершин (x1, y1), (x2, y2), (x3, y3). Проверить, попадает ли точка с координатами (x4, y4) внутрь этого треугольника.
Соединим тестируемую точку (x4, y4) c вершинами треугольника и вычислим сумму площадей образовавшихся треугольников s1+s2+s3 с площадью исходного треугольника s. Очевидно, что точка внутри, если s=s1+s2+s3. Программа использует две функции: Geron() и denka() для вычисления площади треугольника и длины отрезка соответственно.
// Программа отлажена в Borland C++ Builder 6 #include<iostream.h> #include<math.h> #include<conio.h> double Geron (double x, double y, double z) { double p=(x+y+z)/2; return sqrt(p*(p-x)*(p-y)*(p-z)); } double denka(double k, double l, double z, double m) { return sqrt((z-k)*(z-k)+(m-l)*(m-l)); } void main() { float x1,y1,x2,y2,x3,y3,x4,y4,s,a1,a2,a3,a4,a5,a6,s1,s2,s3,s4; cout<<"Введи координаты первой точки "; cin>>x1>>y1; cout<<"Введи координаты второй точки "; cin>>x2>>y2; cout<<"Введи координаты третьей точки "; cin>>x3>>y3; cout<<"Введи координаты тестируемой точки "; cin>>x4>>y4; a1=denka(x3,y3,x1,y1); a2=denka(x3,y3,x2,y2); a3=denka(x2,y2,x1,y1); s=Geron(a1,a3,a2); a4=denka(x4,y4,x2,y2); a5=denka(x4,y4,x1,y1); a6=denka(x4,y4,x3,y3); s1=Geron(a1,a5,a6); s2=Geron(a5,a3,a4); s3=Geron(a2,a6,a4); s4=s1+s2+s3; //cout<<"s="<<s<<endl; //cout<<s1<<endl; cout<<s2<<endl;cout<<s3<<endl; //cout<<"s1+s2+s3="<<s4<<endl; //cout<<"fabs(s-s4)="<<fabs(s-s4)<<endl; if (fabs(s-s4)<0.001) cout<<"Точка лежит в треугольнике"; Else cout<<"Точка не лежит в треугольнике"; cout<<"\n-----------------------------"<<endl; getch(); }
Задача 64. Программа с функцией power() обеспечивает возведение натурального числа А в n-ю степень (n –натуральное число). Результат не должен превосходить 232–1. // Функция находит p=tn unsigned long power(unsigned long t, unsigned long n) { unsigned long p=1; while (n!= 0) { if (n%2!=0) p*=t; n/=2; t*=t; } return (p); }
/* Возведение в степень-главная программа */ #include <stdio.h> #include <conio.h> int main() { int n,a; clrscr(); printf("Введи a, n "); scanf("%d %d",&a,&n); printf("%d в степени %d = %lu\n",a,n,power(a,n)); getch(); return 0; }
Задача 65. Программа с функцией proso() находит в заданном диапазоне [1, m] все простые числа.
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include<conio.h> #include<stdio.h> #include <iostream> using namespace std; #include <math.h> int proso(int k) { int i=3; if(k%2 == 0) return 0; //четное for(i=3;i<k/2; i+=2) if(k%i==0) return 0; return 1; } int main() { int m,i; setlocale(NULL, ".1251"); printf("Введи m "); scanf("%d",&m); for (i=1;i<m;i+=2) if(proso(i)) printf("%d - простое\n",i); return 0; }
Задача 66. Программа позволяет найти в заданном промежутке все совершенные числа. Напомним, что натуральное число называют совершенным, если оно равно сумме всех своих делителей, не считая его самого. Известно, что все совершенные числа — четные и что первое совершенное число из натурального ряда равно 6. Этим объясняется правило изменения параметра внешнего цикла. Так как все натуральные числа имеют своим делителем единицу, полагаем начальное значение суммы делителей числа S = 1. Во внутреннем цикле организуется перебор всех множителей текущего значения N. Из теории чисел известно, что такому испытанию имеет смысл подвергать числа от 2 до N/2, либо даже до. Это не очень совершенный алгоритм. Более эффективный алгоритм будет реализован в следующей задаче. #include <stdio.h> #include <conio.h> #include <dos.h> int main() { unsigned long j,n,M,S; struct time t; clrscr(); printf("ВВЕДИ M\n"); scanf("%lu",&M); n=4; gettime(&t); printf("The current time is: %2d:%02d:%02d.%02d\n", t.ti_hour, t.ti_min, t.ti_sec, t.ti_hund); while (n <= M) { S=1; j=2; while (j <= n/2) { if (n%j == 0) S=S+j; j++; } if (n == S) printf("%lu-СОВЕРШЕННОЕ\n",n); n+=2; } gettime(&t); printf("The current time is: %2d:%02d:%02d.%02d\n", t.ti_hour, t.ti_min, t.ti_sec, t.ti_hund); getch(); return 0; }
В программе использован новый тип данных – структура, который подробно будет обсуждаться позже. Здесь он использован для доступа к служебной структуре, хранящей системное время. – структура
Задача 67. Программа позволяет найти в заданном интервале все совершенные числа. Используется алгоритм нахождения совершенных чисел, более эффективный по сравнению с приведенным ранее. Этот алгоритм основан на известном из теории чисел утверждении Ферма о том, что если натуральное число p = 2k+1 – 1 простое, то число n = 2k.(2k+1 – 1) = p.2k — совершенное (k = 1,2,...). Функция proso определяет, является ли число p простым; функция power() служит для возведения натурального числа в степень и представляет самостоятельный интерес (впрочем, для той же цели подойдет и стандартная функция pow()). Обратите внимание, что функция proso() проверяет в качестве возможных делителей исходного числа только нечетные числа, так как само испытуемое число - нечетное. Отметим, что это очень эффективный алгоритм: приведенные в задаче результаты были получены программой на нашем компьютере (процессор AMD AthlonÔ XP 2000+ 1.7GHz) практически мгновенно. Программа из предыдущей задачи за разумное время этого сделать не может. Вывод: если алгоритм плохой, то программа хорошей быть не может.
// Программа отлажена в Borland C++ Builder 6 /* Найти все совершенные числа, не превосходящие 232 – 1 */ #include <stdio.h> #include <conio.h> #include <math.h> /* Функция возведения t в n-ю степень */ unsigned long power(unsigned long t, unsigned long n) { unsigned long p=1; while (n!= 0) { if (n%2!=0) p=p*t; n/=2; t*=t; } return (p); }
int main() { clrscr(); int proso(unsigned long); unsigned long K,P,N; K=1; while (K <=17) { N = power(2,K); // либо N=pow(2,K); P = 2*N-1; if (proso(P)) printf("%lu-СОВЕРШЕННОЕ\n",N*P); K++; } getch(); return 0; }
/* Подпрограмма определяет, является ли число n простым */ int proso(unsigned long n) { unsigned long i=3; while (i < n/2) { if (n%i == 0) return (0); i+=2; } return (1); }
Результаты: 6-СОВЕРШЕННОЕ 28-СОВЕРШЕННОЕ 496-СОВЕРШЕННОЕ 8128-СОВЕРШЕННОЕ 33550336-СОВЕРШЕННОЕ 4294901760-СОВЕРШЕННОЕ
Далее приведены примеры программ, реализующих некоторые численные методы вычисления корней нелинейных уравнений. Сделаем некоторые предварительные пояснения.
Основные понятия численного решения уравнений Собираясь использовать приближенные методы численного решения уравнений, мы не будем различать алгебраические (рациональные, иррациональные, линейные или нелинейные) и трансцендентные функции. Итак, будем предполагать, что задано уравнение f(x)=0 (1) где функция f(x) – непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b). Требуется решить уравнение (1), т.е. найти множество всех его действительных корней с заданной точностью Универсальные вычислительные алгоритмы основаны на том, что исходят из некоторого начального приближения x0 одного из корней, которое затем улучшают (уточняют) до требуемой точности. Как известно, приближенное нахождение корней нелинейного уравнения f(x)=0 обычно состоит из двух этапов: а) отделение корней уравнения – отыскание достаточно малых отрезков, принадлежащих области определения f(x), в каждом из которых заключен один и только один корень уравнения (1). б) уточнение приближенных корней – вычисление корней с заранее заданной точностью, если известно некоторое его начальное приближение в интервале, не содержащем других корней.
Согласно теореме Больцано-Коши [17], если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, то есть f(a)·f(b) <0, то внутри этого отрезка содержится, по крайней мере, один корень уравнения f(x) = 0, т.е. найдется хотя бы одно число x* Далее, если первая производная f'(x) не меняет знака на отрезке [a; b] (т.е. функция f (x) монотонна), то при выполнении условий теоремы Больцано-Коши уравнение f(x)=0 имеет на этом отрезке единственный корень.
Грубо отделить корни уравнения можно табулированием исследуемой функции. Однако наиболее изящным и эффективным следует признать графический метод при условии, что имеются удобные и надёжные средства построения графиков математических функций. После отделения корней поведение графика функции на отрезке локализации корня может иметь один из следующих вариантов:
Поведение графика функции на отрезке локализации корня имеет существенное значение при программной реализации многих численных методов отыскания корней уравнений (метод Ньютона, метод секущих и др.) Некоторые численные методы уточнения корней уравнения (1) будут реализованы далее.
Задача 68. Метод дихотомии (метод половинного деления). Программа находит с погрешностью e > 0 корень x* уравнения F(x) = 0, где F(x) – непрерывная на отрезке [a, b] функция. Предполагается, что функция удовлетворяет условию F(a)*F(b) < 0, т.е на концах интервала [a, b] функция имеет значения разных знаков, что гарантирует наличие в заданном интервале по крайней мере одного корня уравнения. Для нахождения корня отрезок [a; b] делится пополам точкой c = (a+b)/2 и далее выбирается тот полуинтервал, на концах которого знаки F(x) разные. Затем процесс деления повторяется до тех пор, пока длина интервала не станет меньше e. В качестве x* можно взять, например, средину получившегося интервала. Описанный метод реализуется функцией zero().
// Программа отлажена в Visual Studio 2008 #include "stdafx.h" #include <iostream> #include <math.h> #include <conio.h> using namespace std;
double f(double x);
int main() { double zero(double,double,double); float a,b,eps=1e-5; a=1.2; b=1.5; setlocale(NULL, ".1251"); if(f(a)*f(b)>0) { cout<<"Не могу найти корень"; return 1; } cout<<"Корень равен "<<zero(a,b,eps); getch();return 0; }
double f(double x) { //return x*x-5*x+6; return 2*x-cos(x); }
double zero(double a,double b,double eps) { double c; if(f(a)==0) return a; if(f(b)==0) return b;
while (fabs(b-a)>eps) { c=(a+b)/2; if (f(c)==0) return(c); if (f(a)*f(c)<0) b=c; else a=c; } return (a+b)/2; }
Задача 69. Метод простых итераций. Программа находит корень x* уравнения F(x)=0 на заданном интервале [a, b] c заданной точностью e > 0, где F(x) — непрерывная на [a, b] функция. Предполагается, что F(a)*F(b)<0, т.е. корень находится на отрезке [a, b].
Метод состоит в замене исходного уравнения эквивалентным ему уравнением x = j(x). Это можно сделать всегда, притом не единственным способом (можно, например, прибавить x к левой и правой частям уравнения F(x)=0). Например, уравнение x³–9x+3=0 можно представить так:
1) 3) x= x³ - 8x + 3 4)
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня можно принять, например,
В качестве каждого (k+1)-го приближения берут Полученная последовательность |φ'(x)| ≤ M < 1 для всех х Для конкретной оценки величины М (определяющей скорость сходимости: чем меньше М, тем быстрее сходимость) проще всего пользоваться формулой: М = max |φ'(x)|, где максимум берется по отрезку изоляции корня [a; b].
Оценив φ'(x) для четырех приведенных выше равносильных уравнений, соответствующих уравнению x³–9x+3=0 (учитывая, что корень уравнения заключен в интервале [0, 1]), придем к выводу, что только второе и четвертое уравнения годятся для применения к ним метода итераций; для остальных уравнений итерационный процесс будет расходящимся. Процесс итераций обычно продолжают до тех пор, пока не будет выполнено условие
где Если вычисление производной φ'(x) и ее оценка затруднительны, то можно ограничить число итераций некоторым числом, например n ≤ 500. Приведем здесь два решения поставленной задачи. Первый (упрощеный) вариант не использует оценку производной φ'(x). В контрольном примере (см. текст функции fi(x)) найден один из корней уравнения x – ex + 2 = 0 на отрезке [-2, 0], а именно x1*» ‑1.841402, т. е. тот корень отрезка [a, b], где |j¢(x)| = ex < 1; второй корень этого уравнения x2*» 1.146193.
// Программа отлажена в Borland С++ Builder 6 (8.04.2008) // Вычисление корня F(x)=0 методом простых итераций // упрощенный вариант #include <stdio.h> #include <iostream.h> #include <conio.h> #include <math.h>
// основная программа void main() { int a,b; // наглость, конечно, но прототип согласует типы // формальных и фактических параметров float eps,x; double iterac(double, double, double); clrscr(); a=-2; b=0; eps=0.00001; cout<<"корень = "<<iterac(a,b,eps)<<'\n'; getch(); }
double iterac(double a, double b, double eps) // Эта процедура вычисляет корень уравнения // методом простых итераций { double xn,xn1; int kit=0; double fi(double x); // выбор начального приближения xn= (a+b)/2; do { xn1= fi(xn); if (fabs(xn1 - xn) < eps) break; xn = xn1; kit++; } while (kit<500); if (kit<500) return xn; Else cout<<"Расходящийся процесс..."; }
// вычисление функции double fi(double x) { // return sin(x) + 0.25; return exp(x)-2; }
Ниже приведен более надёжный вариант программы, реализующей метод простых итераций – с оценкой модуля производной φ'(x). // Программа отлажена в Visual Studio 2008 // iterac3.cpp Вычисление корня F(x)=0 методом // простых итераций c оценкой максимума 1-й производной // на [a, b]
#include "stdafx.h" #include <stdio.h> #include <iostream> #include <conio.h> #include <math.h>
// основная программа int main() { double x, a, b,M; const double eps = 1.0e-4; double iterac(double,double,double, double); double dF1(double);
printf("Введи a b "); scanf("%lf %lf", &a, &b);
//оценка maксимума 1-й производной на [a, b]
x=a; M=fabs(dF1(x)); while(x< b) { x=x + eps*10; if(fabs(dF1(x)) > M) M=fabs(dF1(x)); } printf("maximum = %lf\n", M); if(M < 1) printf("корень = %lf\n", iterac(a,b,eps,M)); else printf("Расходящийся процесс..."); getch(); return 0; } double iterac(double a,double b,double eps, double M) // Эта процедура вычисляет корень уравнения // методом простых итераций { double xn,xn1; int kit=0; double F(double x); // {выбор начального приближения} xn= (a+b)/2; do { xn1 = F(xn); if (fabs(xn1 - xn) < M*eps/(1 - M)) break; xn= xn1; kit++; } while(kit<500); return xn; }
// {вычисление функции} double F(double x) { // return sin(x) + 0.25; // return exp(x) - 2; // return x*x*x - 8*x +3; //расходящийся процесс return (x*x*x + 3) / 9; // на [0,1] x=0.337609 }
double dF1(double x) { return (x*x) / 3; //return 3*x*x - 8; // }
Задача 70. Составить программу и функции для вычисления с точностью ε=10-5 значения корня уравнения F(x)=0 на интервале [a, b] методом Ньютона (касательных). Предполагается, что F(a)*F(b)<0, что гарантирует наличие в заданном интервале по крайней мере одного корня уравнения.
Пусть [a; b] – отрезок изоляции корня x* уравнения F(x)=0, F(a) · F(b) <0; функция F(x) непрерывна и дифференцируема на [a; b], производные F '(x), F ''(x) сохраняют знак. Правило применения метода касательных следующее: в качестве начального приближения x0 к корню x* выбирается тот конец отрезка изоляции (x0 = a или x0= b), в котором выполняется условие F( x0 ) · F ''( x0 )>0. Уточнение корня осуществляется по следующей рекуррентной формуле xn+1 = xn –, n = 0, 1, 2…, Если на некотором шаге итерационного процесса окажется, что | x n+1 – x n | ≤ ε, то процесс завершается, и последнее полученное приближение x n+1 принимают за приближенное значение корня с точностью ε. Рассмотреть вариант: x-Sinx-0.25=0 a=1, b=1.5
// Вычисление корня уравнения y=F(x) методом Ньютона (касательных) #include <stdio.h> #include <iostream.h> #include <conio.h> #include <math.h>
// основная программа void main() { float eps,x,a,b; double newton(double, double, double); clrscr(); a=1; b=2; eps=0.00001; cout<<"корень = "<<newton(a,b,eps)<<'\n'; getch(); } double newton(double a, double b, double eps) // Эта процедура вычисляет корень уравнения // методом Ньютона (касательных) { double xn,xn1; double F(double x); double dF1(double x); double dF2(double x); // {выбор начального приближения} if (F(a)*dF2(a) > 0) xn= a; Else xn= b; do { xn1= xn - F(xn) / dF1(xn); if (fabs(xn1 - xn) < eps) break; xn= xn1; } while (1); return xn; } // {вычисление функции} double F(double x) { return x - sin(x) - 0.25; } // {вычисление второй производной} double dF2(double x) { return sin(x); } // {вычисление первой производной} double dF1(double x) { return 1 - cos(x); }
Задача 71. Ниже представлен программный проект, состоящий из нескольких самостоятельных модулей: 1. Вывод треугольника 2. Падающая звезда 3. Рисуем фигуры Для выбора любого из них используется профессиональное меню, с подсветкой выбираемого пункта меню и перемещением подсветки с помощью клавиш управления. Не поленитесь и разберитесь, как устроено это меню. Пригодитс
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.48 (0.019 с.) |

 Пусть требуется вычислить площадь некоторого выпуклого многоугольника, например, четырёхугольника, с заданными длинами сторон a, b, c, d и диагональю f. Задача будет успешно решена, если мы создадим функцию для вычисления площади некоторого абстрактного треугольника со сторонами x, y, z. Тогда, обратившись к ней дважды, вычислим площади S1 и S2 двух треугольников, составляющих в сумме площадь четырехугольника, и проблема будет полностью решена.
Пусть требуется вычислить площадь некоторого выпуклого многоугольника, например, четырёхугольника, с заданными длинами сторон a, b, c, d и диагональю f. Задача будет успешно решена, если мы создадим функцию для вычисления площади некоторого абстрактного треугольника со сторонами x, y, z. Тогда, обратившись к ней дважды, вычислим площади S1 и S2 двух треугольников, составляющих в сумме площадь четырехугольника, и проблема будет полностью решена.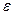 > 0.
> 0. (a; b) такое, что f(x*)=0.
(a; b) такое, что f(x*)=0.
 2)
2) 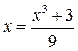


 , к = 0, 1, 2...
, к = 0, 1, 2... сходится к искомому решению х* при возрастании k, если выполняется условие
сходится к искомому решению х* при возрастании k, если выполняется условие ,
,


