
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти все автоморфные числа в заданном числовом интервале.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
// Программа отлажена в Visual Studio 2008 #include<conio.h> #include<stdio.h> #include <iostream> using namespace std;
int main() { long i, n, x, y, lim, divizor;
lim=10; divizor=10; n=1; for(i=1; i <= 4; i++) { for (x=n; x<=lim; x++) { y=x*x; if (y%divizor==x) printf(" x= %ld, y= %ld\n",x,y); } printf("\n"); lim=lim*10; divizor*=10; n=n*10; } getch();return 0; }
Задача 38. Строится трубопровод заданной длины. Имеются трубы двух различных размеров. Вывести сообщение — сколько длинных и сколько коротких труб требуется для строительства? Найти все варианты. Замечание. Задача не всегда имеет решение; если решения нет - вывести сообщение об этом на экран (самостоятельно).
#include <stdlib.h> #include <iostream.h> #include <conio.h> #include <stdio.h> #include <dos.h> int main() { clrscr(); int max, x, y, s, c1, c2, t; t=1; cout<<"Длина трубы 1-го типа? "; cin>>c1; cout<<"Длина трубы 2-го типа? "; cin>>c2; cout<<"Длина трубопровода? "; cin>>s; for (x=0; x<=s/c1; x++) for (y=0; y<=s/c2; y++) if (c1*x+c2*y==s) {cout<<" Длинные трубы - "<<y<<" Короткие трубы - "<<x<<"\n";} getch(); return 0; }
Задача 39. Есть отрезки труб длиной a метров и b метров (a < b). Сколько тех и других потребуется, чтобы проложить трубопровод заданной длины T с минимальным числом сварных швов? (Трубы разрезать нельзя!). Замечание. Задача всегда имеет решение при a=3, b=5, если T>7. #include <stdio.h> #include <iostream.h> #include <conio.h> int main() { int t3,t5,T; int a=3,b=5; clrscr(); printf("длина трубопровода?"); cin>>T; t3=0; while (t3<=T/a) { t5=(T-a*t3)/b; if (a*t3+b*t5 == T) {cout<<a<<"-м: "<<t3<<endl; cout<<b<<"-м: "<<t5<<endl; break; } Else t3++; } if (t3>T/a) cout<<"Нельзя построить"; getch(); return 0;
}
Задача 40. Программа определяет все двузначные числа, делящиеся без остатка на сумму своих цифр и выводит их на экран так, что числа каждого десятка находятся в новой строке. #include <iostream.h> #include <conio.h> int main() { clrscr(); int x, y, t; for (x=1; x<=9; x++) { cout<<"\n"; for (y=0; y<=9; y++) if ((x*10+y)%(x+y) == 0) cout<<x<<y<<" "; } getch(); return 0; }
Задача 41. Программа реализует правило, согласно которому покупателю с 1 гривны всегда выдаётся сдача наименьшим количеством монет. Например, если стоимость покупки 24 коп., то продавец, руководствуясь этим правилом, должен дать сдачу набором монет: 50, 25, 1.
#include <stdio.h>
#include <conio.h> #include <dos.h> int main () { int t,s; clrscr(); printf("Сколько стоит покупка?"); scanf("%d",&s); t = 100-s; printf("Вот ваша сдача:"); while (t>=50) { t-=50; printf(" 50 "); } while (t>=25) { t-=25; printf(" 25 "); } while (t>=10) { t-=10; printf(" 10 "); } while (t>=5) { t-=5; printf(" 5 "); } while (t>=2) { t-=2; printf(" 2 "); } while (t>=1) { t-=1; printf(" 1 "); } getch(); return 0;
}
Задача 42. Программа позволяет получить на экране двоичное представление введенного по запросу символа. Используются команды логического умножения (&) и сдвига (>>). Функция putchar() выводит на экран один символ. void main() { unsigned char c,mask=0x80; clrscr(); printf("Введи символ "); c=getch(); printf("%c = ",c); while (mask) { if (c&mask) putchar('1'); Else putchar('0'); mask>>=1; } getch(); return 0; }
Задача 43. Программа позволяет получить на экране равнобедренный треугольник заданной высоты N, сплошь заполненный символом “*”.
// Программа отлажена в Borland C++ Builder 6 #include <stdio.h> #include <conio.h> #include <iostream.h> #include <stdlib.h> int main() { int k,n,m,x,y; clrscr(); cout<<"Введи высоту ==> "; cin>>n; x=40,y=1; m=1; while (m<=n) { gotoxy(x--,y++); //позиционирование курсора k=1; while (k<=2*m-1) { cout<<"*"; k++; } m++; } getch(); return 0; }
Задача 44. Символ с кодом 002 “взлетает” с нижней строки экрана, предварительно заполненной символом “=” и медленно поднимается вверх. // Программа отлажена в Borland C++ Builder 6 #include<iostream.h> #include<stdio.h> #include<conio.h> #include<dos.h> int main() { int k; char ch='\002'; clrscr(); gotoxy(1,24); for (k=1;k<80;k++) cout<<"="; for (k=24;k>0;k--) { gotoxy(40,k); //позиционирование курсора putch(ch); Sleep(500); gotoxy(40,k); putch(' '); //стереть символ } getch(); return 0;
}
Задача 45. Программа-секундомер. В центре экрана выводятся числа от 1 до 60, последовательно сменяющие друг друга через 1 сек. Вывод осуществляется в маленьком окне, закрашенном коричневым цветом; цвет цифр жёлтый. Задержку выполнения программы на заданное число миллисекунд осуществляет библиотечная функция функция Sleep().
// Программа отлажена в Borkfnd С++ Builder 6 (1.04.2008) #include <iostream.h> #include <conio.h>
int main() { int k=1; textbackground(0); //восстановить фон clrscr(); window(36,12,43,12); //"форточка" в центре textbackground(6); textcolor(14); clrscr(); while (k<=60 &&!kbhit()) { gotoxy(2,1); cprintf("%d cek",k++); //cout<<k++<<" сек";
//Задержка выполнения программы на //заданное число миллисек Sleep(1000); } return 0;
}
Задача 46. Программа в центре экрана последовательно с интервалом в 0.5 сек. выводит символы «–», «\», «|», «/», имитируя вращение малого пропеллера. Процесс длится, пока не нажата какая-нибудь клавиша. Эту ситуацию контролирует стандартная функция kbhit(). Для приостановки выполнения программы на 0.1 сек. применена функция Sleep ().
// Программа отлажена в Borland С++ Builder 6. 1.04.2008 #include <iostream.h> #include <conio.h> #include <stdio.h> int main() { char a='\-', b='\\',c='\|',d='\/'; clrscr(); double msk=100; do { gotoxy(40,12); cout<<a<<'\007'; Sleep(msk); gotoxy(40,12); cout<<b<<'\007'; Sleep(msk); gotoxy(40,12); cout<<c<<'\007'; Sleep(msk); gotoxy(40,12); cout<<d<<'\007'; Sleep(msk); } while (!kbhit()); getch(); return 0; }
Задача 47. Символ с кодом 002 ("рожица") движется по экрану вдоль главной диагонали.
// Программа отлажена в Borland C++ Builder 6 #include<iostream.h> #include<conio.h> #include<dos.h> int main() { int x=1, y=1; char ch='\002'; clrscr(); while (y<=24) { gotoxy(x,y); //курсор в точку x,y cout<<(ch); //вывод символа Sleep(300); //пауза clrscr(); //очистка экрана gotoxy(45,24); cout<<"\t\t---------------------"; x+=3; y++; } getch(); return 0; }
Задача 48. Найти все трехзначные натуральные числа, которые делятся без остатка на сумму своих цифр #include <iostream.h> #include <conio.h> int main() { clrscr(); int a=100, z1, z2, z3; while (a<=999) { z3=a%10; // последняя цифра z1=a/100; // первая цифра z2=a/10%10; // средняя цифра if (a%(z1+z3+z2) == 0) cout<<a++<<" "; } getch(); return 0; }
Задача 49. Программа генерирует случайную последовательность латинских прописных букв, которые появляются в произвольных местах на экране и исчезают через T сек. Старайтесь нажимать на клавишу, которая соответствует символу на экране. Конец игры — ESC. По завершении программа выводит количество правильных и неправильных ответов // Программа отлажена в Borland C++ Builder 6 #include <stdlib.h> #include <iostream.h> #include <conio.h> #include <time.h> #include <dos.h> int main() { char ch,s; int T=5; int kp=0, // к-во правильных и kn=0; // к-во неправильных ответов randomize(); clrscr(); do { s=random(26)+65; //случайная буква gotoxy(random(78)+1,random(23)+1); putch(s); Sleep(T*1000); clrscr(); cout<<"Что смотришь? Теперь жми наугад"; ch=getch(); clrscr(); if (ch==s) kp++; Else kn++; } while (ch!=27); clrscr(); cout<<"правильных - "<<kp<<endl; cout<<"неправильных - "<<kn-1<<endl; getch(); return 0; }
Задача 50. Программа генерирует случайную последовательность латинских прописных букв, которые появляются в произвольных строках на экране и движутся слева направо. Старайтесь нажимать на клавишу, которая соответствует символу на экране. Угаданный символ падает вниз, а при неверно нажатой клавише на его месте появляется символ с кодом 002. Конец игры — ESC. По завершении программа выводит количество правильных и неправильных ответов.
// Программа отлажена в Borland C++ Builder 6 #include <stdlib.h> #include <iostream.h> #include <conio.h> #include <time.h> #include <dos.h> int main() { char ch,s; int y,x,kp=0, kn=0;// к-во правильных и // к-во неправильных ответов randomize(); clrscr(); do { clrscr(); s = random(26)+65; //случайная буква x = 1; y = random(23)+1;
do { gotoxy(x,y); putch(s); Sleep(500); clrscr(); x++; } while (!kbhit());
// Очень ВАЖНО! getch() выбирает из буфера // символ, оставленный функцией kbhit()
ch=getch(); if (ch == s || ch == s+32) { while (y<25) { gotoxy(x,y); putch(s); Sleep(250); clrscr(); y++; } kp++; } Else { if(ch == 27) break; kn++; gotoxy(x,y); putch('\002'); Sleep(3500); clrscr(); } } while (ch!= 27); //ESC clrscr(); cout<<"правильных - "<<kp<<endl; cout<<"неправильных - "<<kn<<endl;
getch(); return 0; }
Задачи для самостоятельного решения
1. Используя оператор цикла: а) напечатайте в 12-й строке экрана последовательность чисел 23 21 19 17 … 3 1, б) напечатайте эти же числа вдоль главной диагонали экрана: ….. в) напечатайте эти же числа вдоль побочной диагонали экрана: …. 2. Напечатайте все двузначные натуральные числа, сумма цифр которых равна 8.
3. Напечатайте все трехзначные натуральные числа, в которых средняя цифра равна сумме крайних цифр.
4. Построить в центре экрана малое текстовое окно размером 3х5 символов, закрасив его малиновым цветом. Используя оператор цикла, организовать вывод в центр этого окна разноцветной последовательности сменяющих друг друга символов ª © ¨ «с кодами 3, 4, 5 и 6 соответственно. Вывод завершается про нажатии любой клавиши.
5. Организуйте вывод символа ¨, который движется вдоль главной диагонали экрана.
6. Организуйте вывод символа ¨, который движется вдоль побочной диагонали экрана 7. Составить таблицу значений простых чисел, вычисляя их по соотношениям: y = 4x2 – 162x + 1681, y = 9x2 – 249x + 1763, если
8. Получить таблицу температур по Цельсию от 0 до 100 градусов и их эквивалентов по шкале Фаренгейта, используя для перевода формулу:
9. Найти и напечатать все трёхзначные натуральные числа, делящиеся на а) каждую из своих цифр(кроме 0); б) сумму своих цифр. 10. Дано натуральное число m (m < 27). Получить все трёхзначные натуральные числа, сумма цифр которых равна m. 11. Получить все трёхзначные натуральные числа, сумма цифр которых равна их произведению. 12. Получить все трёхзначные натуральные числа, в которых сумма крайних цифр равна средней цифре.
13. Составить программы для решения следующих задач: a) Символ © движется в 40-й колонке экрана сверху вниз, а затем символ ª, в этой же колонке движется снизу вверх. б) Одновременно в 38-колонке экрана символ © движется сверху вниз, а в 40-й колонке символ ª движется снизу вверх. в) В 40-й колонке навстречу друг другу движутся символы © и ª. В месте их столкновения появляется слово “ БАБАХ”.
14. Составить программу, которая последовательно вводит по одному числу и находит максимальное из введённых чисел. Признак конца - ввод нуля.
15. Составить программу, которая последовательно вводит по одному целому числу и находит отдельно сумму чётных и сумму нечётных чисел. Процесс продолжается до ввода нуля.
16. Составить программу, которая последовательно вводит по одному числу и находит отдельно сумму положительных и сумму отрицательных чисел. Процесс продолжается до ввода нуля.
17. Некий предприниматель хочет приобрести недвижимость общей стоимостью в N гривен. Он располагает суммой в S гривен, а его бизнес приносит ему ежемесячно доход в D гривен. Составить программу, которая определяет начальные величины N, S и D, и показывает (выводит на экран) динамику накопления денег от месяца к месяцу и определяет количество месяцев, необходимых для накопления нужной суммы.
18. Найти и напечатать все трёхзначные натуральные числа, сумма кубов цифр которых равна самому числу.
19. Найти все трёхзначные натуральные числа, сумма цифр которых равна заданному числу m (m <= 27).
20. Ввести последовательность из n действительных чисел и найти среднее арифметическое положительных чисел из введённой последовательности.
21. Напечатать в возрастающем порядке все трёхзначные натуральные числа, в десятичной записи которых нет одинаковых цифр.
22. Составить программу, которая определяет различные возможные способы размена 1 гривны. Предполагается, что в обращении имеются монеты следующего достоинства: 50, 25, 10, 5, 2 и 1 коп
23. Груз перевозят в трёх — и пятитонных автомобилях. Сколько тех и других потребуется для перевозки T тонн груза? Найти все возможные варианты.
24. Получить все шестизначные «счастливые» номера, т.е. такие натуральные числа, у которых сумма его первых трёх цифр равна сумме трёх последних цифр.
25. Составить программу, реализующую правило, по которому покупателю со 100 гривен при покупке товара всегда выдаётся сдача наименьшим количеством купюр. Считать, что в обиходе есть купюры достоинством: 50, 20, 10, 5, 2 и 1 гривны.
26. Предприятие выплачивает своим работникам надбавку к основной зарплате, которая зависит от стажа их работы. Соответствующие зависимости сведены в таблицу.
Стаж Надбавка, % до 5 лет 0 от 5 до 10 лет 10 свыше 10 лет 15 Составить программу, которая последовательно запрашивает размер основной зарплаты и стаж работающего, а затем вычисляет и выводит сумму надбавки и общую зарплату с учётом надбавки. Число служащих не превышает 30.
27. Поступающее на элеватор зерно проверяют на влажность. Если она превышает 20%, то первоначальный вес зерна уменьшают на 7%. Составить программу, в которой последовательно запрашивают вес зерна и его влажность, а затем вычисляют и печатают вес зерна, поступивший в зачёт. Число поставщиков = 20.
28. Плата за пользование электроэнергией исчисляется по следующему правилу: за первые 90 квт/ч взыскивается по 6.5 коп, за каждый израсходованный киловатт-час, а за каждый последующий — в два раза больше. Составить программу, которая последовательно (в цикле) по запросу вводит количество израсходованной в месяц эл. энергии, вычисляет и выводит начисленную к оплате сумму. Число плательщиков = 29.
29. При таможенном досмотре с пассажира взыскивают госпошлину, которая составляет 5% от общей стоимости провозимых им товаров, если последняя превышает 1400 долларов. Составить программу, которая последовательно вводит по запросу стоимость провозимых товаров для каждого пассажира и вычисляет сумму пошлины. Всего пассажиров не более 30.
30. Закройщик ателье получает надбавку к зарплате, если он достиг определённой экономии материала. Соответствующие зависимости показаны в таблице:
Отходы, % Надбавка, % 5 17 10 12 15 7
Составить программу, которая запрашивает последовательно (в цикле) зарплату закройщика и достигнутую им экономию материала, а затем вычисляет его надбавку к его зарплате и общую зарплату (с надбавкой).
31. Ввести натуральное число n(n<=65535). Найти и выдать на экран сумму его цифр. 32. Найти наибольший общий делитель двух заданных чисел. 33. Найти наименьшее общее кратное двух заданных чисел.
Итерационные циклы Итерационными традиционно называют циклы, в которых количество повторений тела цикла заранее неизвестно и цикл завершается обычно по достижении нужной точности вычислений. При этом обычно вычисления ведутся по одной и той же формуле вида
когда полученное на предыдущем шаге значение используется на последующем шаге.
Покажем на примерах наиболее существенные моменты, связанные с итерационными циклами.
Задача 51. Вычислить приближенно, с заданной точностью e = 0.001 значение функции y = (a > 0) без привлечения библиотечной функции sqrt().
Для решения задачи воспользуемся итерационной формулой Ньютона: yn+1 = 0.5 (yn + Эта формула позволяет вычислять очередной член последовательности { yn } через уже вычисленный предыдущий член, начиная с некоторого начального приближения y0 > 0. Можно, например, принять y0=. В математике доказано, что такая последовательность сходится к точному значению. Поскольку мы не можем позволить себе (да и не надо, наверное) строить бесконечную последовательность приближений y0, y1,.., yn,..., то процесс обрывается при некотором n таким образом, чтобы погрешность вычисления y = не превышала заданной величины e > 0. Будем считать, что требуемая точность достигнута, если
| yn+1 – yn | £ e Из итерационной формулы Ньютона следует, что предыдущее условие можно записать в следующей эквивалентной форме: | yn+1 – yn | = 0.5| С учетом всего вышесказанного соответствующая программа может иметь такой вид:
#include <math.h> #include <stdio.h> #include <conio.h> int main() { double a, y, y0, v, eps=0.0001; m1: printf("введи a > 0 "); scanf("%lf",&a); if(a <= 0) goto m1; y0=a/2; y=y0;
do { v = 0.5*(a/y - y); y = y + v; } while(fabs(v)>eps);
printf("По итерационной формуле корень из %8.2lf = %lf\n",a, y); printf("По стандартной функции sqrt(%8.2lf) = %lf\n",a, sqrt(a)); getch(); return 0; }
По итерационной схеме вычисляют многие элементарные функции, используя их разложение в степенные ряды (ряды Тейлора–Маклорена), например:
ex = 1 + + + … + + … (1)
cos x = 1 – + – … +(–1)n + … (2)
sin x = x – + – … +(–1)n + … (3)
arctg x = x – + – … +(–1)n +… (|x|<1) (4)
ln(1+x) = x – + – … +(–1)n–1 + … (|x|<1) (5)
При вычислении с помощью степенных рядов удобно пользоваться рекуррентными соотношениями, которые позволяют вычислять очередное слагаемое не непосредственно (это было бы слишком примитивно), а через уже вычисленное предыдущее слагаемое. Прямое вычисление очередного слагаемого может привести к непредсказуемым результатам: при возведении в степень и вычислении факториала можно получить очень большие числа; при делении таких чисел друг на друга произойдет потеря точности, так как количество значащих цифр, хранимых в ячейке памяти, ограничено. Для приведенных выше рядов рекуррентные соотношения могут быть выведены непосредственно: достаточно взять отношение двух соседних слагаемых. Например, для разложения функции ex, общий член ряда которой равен un =, получим:
= =, n=0,1,2,3… (6)
или: un+1 = un. Последнее соотношение уже удобно использовать для вычисления значений очередных слагаемых через предыдущие. И ещё одно замечание. При вычислениях с помощью степенных рядов мы ограничиваемся конечным числом слагаемых, заменяя сумму ряда его частичной суммой
Sn= S0 + S1 + S2 +… +Sn-1 , Sn+1 = Sn + un+1, n = 0,1,2,3… (7) Для сходящегося ряда модуль un при увеличении n стремится к нулю.Возникает практический вопрос: сколько членов ряда нужно сохранить, чтобы получившаяся погрешность вычислений не превышала заданную? Для знакопеременных рядов ответ на поставленный вопрос даёт т. н. правило Лейбница: при замене суммы ряда его частичной суммой Sn имеет место погрешность, не превышающая по модулю величины первого из отброшенных слагаемых. Таким образом, вычисление приближённого значения функции с заданной точностью e можно прекратить, если |un+1| £ e (8) Воспользуемся этими рассуждениями, чтобы вычислить приближённое значение функции y = sin x, предполагая, что |x|<2p. (Этого всегда можно добиться, используя формулы приведения). Формула (3) может быть запрограммирована в виде итерационного процесса, который описывается следующими рекуррентными соотношениями. un+1 = un , Sn+1 = Sn + un+1 . Момент окончания вычислений наступит при |un+1| £ e.
Задача 52. Вычислить приближённо, с точностью e = 0.0001 значение функции y = Sinx, используя описанный выше итерационный процесс. Результат сравнить со значением, полученным с помощью стандартной функции sin(x).
#include<conio.h> #include<iostream> #include <math.h>
using namespace std; #define eps 0.0001
void main () {
int n;
double x,s,u; printf("введи x\n"); scanf("%lf",&x); //cin>>x; printf("%f %lf\n", x,x);
u=x;s=u; n=0; while(fabs(u)>eps) { u=-(u*x*x)/(2*n+2)/(2*n+3); s+=u;n++; } printf("Вычисленное значение Sin(%lf):\n",x); printf("А) По итерационной формуле - %lf\n",s); printf("Б) По стандартной функции - %lf\n",sin(x)); getch(); }
Задачи для самостоятельного решения
1. Вычислить приближённое значение бесконечной суммы S = + + + … Вычисления прекратить, когда очередное слагаемое станет меньше заданного числа e = 0.001.
2. Вычислить приближённое значение числа p, используя соотношения: a) = × × × × … (формула Валлиса). b) = 1 + + + + … c)= × × … d) = × × × × …
3. Вычислить приближенно с заданной точностью e = 0.001, не пользуясь стандартными функциями языка C/C++: y = 4. Вычислить приближенно с заданной точностью e = 0.001 значение функции y = по итерационной формулеyi+1 = 1.5yi – 0.5xyi3, i = 0,1,2,3,… Принять y0 =. Считать, что требуемая точность достигнута, если |yi+1 – yi| £ e.
5. Вычислить приближенно с заданной точностью e = 0.001 значение функции y = Использовать итерационную формулу Ньютона: yi+1 = yi + Принять y0 =
Сравнить полученный результат со значением, вычисленным по соответствующей стандартной библиотечной функции языка С/С++ (pow (a, 1/p)).
6. Выдать на экран в виде таблицы значения функции F(x), заданной в с помощью ряда Тейлора, вычисленные приближенно с заданной точностью e = 0.001 на отрезке [a, b] с шагом Dx. Каждая строка таблицы должна содержать значение аргумента x,значение функции F(x) и количество просуммированных членов ряда.
6.1. e–x = = 1 – + – … + (–1)n + …, |x|<¥
6.2. cos x = = 1 – + – …, |x|<¥
6.3. = = 1 – + – …, |x|<¥
6.4. arctg x= = x – + – …, |x| £ 1 6.5. ln(1 + x) = = x – + – …, –1 < |x| £ 1 6.6. ln = = 2(x + + + …), |x| < 1 6.7. ln(1 – x) = –= –(x + + + …), –1 £ |x| < 1 6.8. ln = 2= 2(+ + + …), |x| > 1 6.9. arctg x = – + = – – + – + …, x < –1 6.10. arctg x = + = – x + – + …, |x| £ 1 6.11. arctg x = + = – + – + …, x > 1 6.12. e–x2= = 1 – + – … + (–1)n + …, |x|<¥ 6.13. ln x = 2= 2(+ + + …), |x| > 0 6.14. ln x = = (x – 1) – + – …, 0 < |x| £ 2
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1073; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.254.182 (0.016 с.) |

 изменяется от 1 до 40 с шагом 1.
изменяется от 1 до 40 с шагом 1.

 ,
, ) = yn + 0.5 (
) = yn + 0.5 (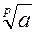 (a > 0, p > 0 целое)
(a > 0, p > 0 целое) (
( – yi), i = 0,1,2,3,…
– yi), i = 0,1,2,3,… . Считать, что требуемая точность достигнута, если | yi+1 – yi | £ e.
. Считать, что требуемая точность достигнута, если | yi+1 – yi | £ e.


