
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число. Раціональні, ірраціональні та дійсні числа.Содержание книги Поиск на нашем сайте
Леонардо да Вінчі
Сучасне твердження: “Будь яка наука досягає значного успіху, якщо використовує у своєму розвитку математичні методи і моделі”.
Вступ Предмет математики Кожна наука, яка вивчає ті чи інші явища оточуючого нас світу, має справу з притаманними їм величинами. Так, фізика – наука про найзагальніші форми руху матерії (механічної, теплової, електромагнітної та ін.) – торкається таких величин, як довжина, сила, температура, маса, питома вага, швидкість, прискорення, теплоємність, сила електричного струму та ін. Незважаючи на надзвичайну різноманітність цих величин, всі вони мають одну спільну властивість: кожну величину можна виміряти, тобто порівняти з певною величиною тієї ж природи, взятою за одиницю міри. Так, довжина вимірюється одиницею довжини – метром, температура – одиницею температури – градусом, сила струму – ампером і т. д. Абстрактне число, що його дістаємо внаслідок вимірювання конкретної величини одиницею масштабу, звуть вартістю, чи значенням величини, яка вимірюється. Якщо взяти будь-який закон природи, приміром закон Ленца-Джоуля про кількість виділюваного тепла при проходженні електричного струму в провіднику Крім поняття числа із світу, який оточує людину, запозичено також поняття фігури. У світі існують різні речі, що мають певну форму і ці форми повинні були піддаватися порівнянню, перше ніж можна було дійти до поняття фігури. Враховуючи сказане, можна дати таке означення предмету математики: математика має за свій об’єкт просторові форми і кількісні співвідношення реального світу. Як і в шкільному курсі (геометрії, алгебри, тригонометрії), так і в математичних дисциплінах вищої школи ці дві сторони – просторові форми і кількісні співвідношення – єдиної математики вимальовуються досить чітко і окреслено: аналітична геометрія вивчає просторові образи, диференціальне та інтегральне числення – кількісні співвідношення. Але за самим означенням, аналітична геометрія – це наука, що вивчає властивості геометричних образів засобами алгебри, тобто геометричні питання “перекладаються” на мову алгебри і зрештою зводяться до кількісних співвідношень, до певних обчислень. З другого боку, в диференціальному та інтегральному численні майже завжди вдаються до геометричного тлумачення тієї чи іншої теореми, користуючись поняттями аналітичної геометрії, та до застосувань до геометрії тих чи інших здобутих результатів. Глибокий взаємозв’язок геометрії й математичного аналізу та їх взаємопроникнення – характерна риса сучасної математики. Сукупність усіх раціональних та ірраціональних чисел звуть дійсними числами. Усі дійсні числа впорядковані за величиною, тобто для будь-яких двох чисел Абсолютна вартість числа. Абсолютною вартістю (або модулем) числа а зветься арифметична вартість цього числа
Властивості: За самим означенням 1. 2. Якщо 3. Доведення: Запишемо очевидні нерівності:
Метод математичної індукції поширює цю властивість на любу кількість доданків. 4. (Абсолютна вартість різниці не менша різниці абсолютних вартостей цих чисел). Доведення: Рівності Сталі і змінні величини. Величина зветься змінною, якщо вона може набирати різні числові вартості в умовах даної задачі. Сталою величиною звуть величину, яка має цілком певну вартість в умовах даної задачі або за будь-яких умов. Область змінювання змінної величини. Сукупність усіх числових вартостей, що їх може набувати змінна х, звуть областю чи обсягом змінювання цієї змінної. Приклад – радіус кола: Функціональна залежність. При дослідженні різноманітних явищ нас цікавлять не стільки змінні величини, взяті кожна окремо, скільки зв’язок між ними та залежність одних величин від інших. Абстрагуючись від конкретних залежностей між конкретними величинами, дамо означення функції. Нехай Х і У – деякі числові множини, а х і у – числа, які їм належать.
Змінна у зветься функцією змінної х, якщо будь-якій вартості х є Х за деяким правилом чи законом ставиться у відповідність одна певна вартість у є У. Це означення однозначної функції. Коли у відповідність х ставиться 2 чи більше вартостей у, то у звуть дво- або багатозначною функцією. Змінна х – аргумент, або незалежна змінна, у – функція, або залежна змінна. Символічний запис
Множина Х – область визначення функції, У – множина її значень. Функція, яка визначається з функціональної залежності Дану функцію Окремі вартості функції Приклад 1. Приклад 2. Відкритий проміжок, для якого дана точка, а є його серединою (центром) зветься околом цієї точки. Всі точки х, які справджують нерівність Границя функції Поняття границі функції – одне з найважливіших у вищій математиці. Нехай на деякій множині Χ визначена функція Означення. Число А називається границею функції 0 < виконується нерівність
Приклад 1. Покажемо, що функція Щоб це довести, ми повинні згідно з означенням для довільного ε > 0 вказати таке δ > 0, при якому із нерівності
Розглянемо Отже, оскільки Таким чином нерівність
виконується завжди для δ < ε. Тоді згідно з означенням Насправді визначення границі рідко використовується при обчисленні границь. Приклад 2. Знайти
Приклад 3. Знайти
Існують дві визначальні границі: 1. 2. Приклад 4. Знайти
Приклад 5. Знайти
Приклад 6. Знайти
Функція
Точка Якщо функція
Формула Тейлора. Нехай функція
Отже, формула Тейлора надає можливість розкласти функцію Зауваження. Формулою Маклорена називають формулу Тейлора (17) при Приклад 1. Знайти Маємо невизначеність
Тоді маємо:
Приклад 2. Знайти Маємо невизначеність
Асимптоти графіка функцій Нехай функція Точка екстемуму Крім того, у точці локального мінімуму (максимуму) справедливе співвідношення Точка Приклад 1. Дослідити функцію
Рис. 3.1. Дослідження функції
Рис. 3.2. Дослідження функції
Дослідимо, чи має дана функція точку перегину. Для цього знайдемо другу похідну і прирівняємо її до нуля: Рис. 3.2 видно, що
2
-4 -2 -1 0 1 2 Рис. 3.3. Графік функції
При дослідженні поведінки функції на нескінченності та поблизу точок розриву (невизначеності) часто виявляється, що графік функції як завгодно близько наближається до тієї чи іншої прямої. Такі прямі називаються асимптотами. Існують три види асимптот: вертикальні, горизонтальні і нахилені. Пряма
Якщо коефіцієнт Пряма Приклад 2. Знайти асимптоти графіка функції За формулою (18) знаходимо коефіцієнти
Отже, пряма Нарешті, точка
-10
-2 -1 0 1 2
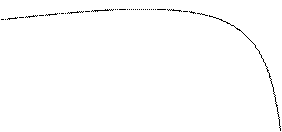
Рис. 3.4. Графік функції Наведемо загальну схему для побудови графіка функції 1. Знайти область визначення функції. 2. Знайти точки перетину графіка функції з віссю ординат (покласти у формулі, яка задає функцію, х = 0) і віссю абсцис (розв’язати рівняння 3. Знайти асимптоти функції. 4. Дослідити функцію на екстремум: знайти точки мінімуму, максимуму, а також точки перегину. Обчислити значення функції у цих точках. Встановити ділянки монотонності функції. 5. Побудувати схематичний графік функції При побудові графіка важливо врахувати його симетрію. Для цього корисно перевірити функцію на парність (непарність). Зауваження. Функція Також важливо перевірити функцію на періодичність: Приклад 3. Побудувати графік функції Згідно з наведеною вище схемою: 1. Область визначення функції 2. Графік даної функції перетинає вісь ординат у точці 3. Дослідимо поведінку функції поблизу точки розриву х = 1. Маємо:
Рис. 3.5. Дослідження функції Отже, пряма 4. Знайдемо першу похідну функції і прирівняємо її до нуля:
Відмітивши ці точки на осі х (Рис. 3.5), дослідимо їх на екстремум. Отже,
5. Дана функція не є парною і не є непарною. Її графік наведено на Рис. 3.6.
-2 -1 0 1 2 3
Рис. 3.6. Графік функції Градієнт функції. Нехай задано закон Приклад 1. Розглянемо функцію двох змінних Нехай функція Приклад 2. Знайти частинні похідні першого порядку від функції
Приклад 3. Знайти частинні похідні другого порядку від функції Для цього знайдемо спочатку частинні похідні першого порядку:
Далі отримуємо:
Зауваження. Похідні Для характеристики швидкості зміни функції в точці
Приклад 4. Обчислити похідну функції Спочатку знайдемо координати одиничного вектора
За формулою (19) маємо: Градієнтом функції
Зауваження. У просторі градієнт функції
З урахуванням виразу (20) формулу (19) можна переписати так
де Отже, градієнт функції Метод найменших квадратів.
Нехай функція
Нехай у точці
Тоді (достатня умова екстремуму): 1). якщо 2). якщо 3). якщо
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.011 с.) |

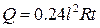 , то він дає нам співвідношення між величинами, точніше співвідношення між числами, що виражають ці величини. Предметом дослідження математики і є якраз числа та різні співвідношення між ними, незалежно від того, які саме конкретні величини чи закони привели нас до цих чисел та їх співвідношень. Отже, абстрагуючись від індивідуальних властивостей тієї чи іншої конкретної величини і беручи до уваги тільки одну спільну властивість усіх величин, що про неї вже була мова, у математиці розглядають величину взагалі, і завдяки цьому створюють загальні теорії, застосовні до величин різноманітної природи.
, то він дає нам співвідношення між величинами, точніше співвідношення між числами, що виражають ці величини. Предметом дослідження математики і є якраз числа та різні співвідношення між ними, незалежно від того, які саме конкретні величини чи закони привели нас до цих чисел та їх співвідношень. Отже, абстрагуючись від індивідуальних властивостей тієї чи іншої конкретної величини і беручи до уваги тільки одну спільну властивість усіх величин, що про неї вже була мова, у математиці розглядають величину взагалі, і завдяки цьому створюють загальні теорії, застосовні до величин різноманітної природи. і
і  справедливе одне з трьох співвідношень
справедливе одне з трьох співвідношень  ;
;  ;
;  .
.
 .
. .
. .
.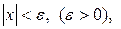 то
то  . Зокрема, коли
. Зокрема, коли  то
то  або
або  .
. .
. і
і 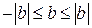 . Додамо їх почленно
. Додамо їх почленно (рівносильне)
(рівносильне)  .
. .
.
 і
і  майже очевидні і на них спинятися не будемо.
майже очевидні і на них спинятися не будемо.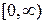 .
. .
. - характеристика функції, вона позначає те правило чи закон, який визначає у як функцію від х.
- характеристика функції, вона позначає те правило чи закон, який визначає у як функцію від х. зветься оберненою щодо даної функції
зветься оберненою щодо даної функції 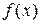 .
. часто звуть прямою. Очевидно, функції
часто звуть прямою. Очевидно, функції 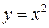 – пряма функція, а
– пряма функція, а  – їй обернена. Остання є двозначною.
– їй обернена. Остання є двозначною. і т.п. позначають символами
і т.п. позначають символами 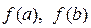 .
. ,
,  і
і 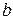 – дійсні,
– дійсні, 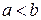 . Функція визначена для таких вартостей х, які справджують нерівності
. Функція визначена для таких вартостей х, які справджують нерівності 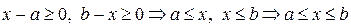 . Таким чином, для всіх вартостей х, між
. Таким чином, для всіх вартостей х, між  та
та  , функція у має дійсні вартості. Тут Х – це
, функція у має дійсні вартості. Тут Х – це  – замкнений проміжок.
– замкнений проміжок. . Функція визначена при
. Функція визначена при  , або
, або  . Тут Х – відкритий проміжок, або інтервал
. Тут Х – відкритий проміжок, або інтервал 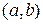 .
. , складають окіл точки
, складають окіл точки  .
.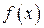 при
при  (або у точці
(або у точці 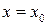 ), якщо для будь-якого ε > 0 можна знайти таке число
), якщо для будь-якого ε > 0 можна знайти таке число  > 0, що при всіх
> 0, що при всіх  , які задовольняють нерівність
, які задовольняють нерівність <
<  ,
, <
<  .
. має в точці
має в точці  0 границю, яка дорівнює 1.
0 границю, яка дорівнює 1. < δ випливала б нерівність
< δ випливала б нерівність < ε.
< ε.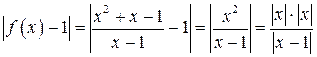 <
<  <1.
<1. .
.




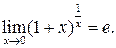
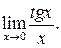







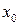 , якщо границя функції дорівнює її значенню в цій точці, тобто:
, якщо границя функції дорівнює її значенню в цій точці, тобто: (1)
(1) , що (за теоремою Вейєрштрасса)
, що (за теоремою Вейєрштрасса)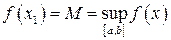 і
і 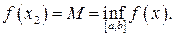 (2)
(2) 
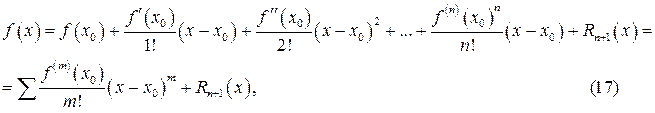 де
де 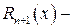 деякий залишковий член, причому
деякий залишковий член, причому 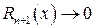 при
при  (0!=1 у формулі (17)).
(0!=1 у формулі (17)). .
. .
. . Розкладемо функції
. Розкладемо функції 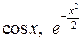 і
і 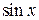 у ряд Маклорена з необхідною точністю:
у ряд Маклорена з необхідною точністю:


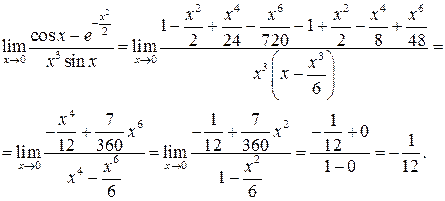
 .
.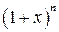 в ряд Маклорена:
в ряд Маклорена: 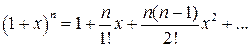 У результаті отримуємо:
У результаті отримуємо: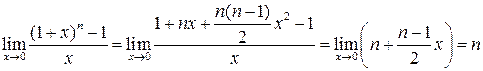 .
. називається точкою екстремуму, якщо
називається точкою екстремуму, якщо 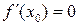 .
.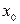 називається локальним мінімумом (максимумом), якщо
називається локальним мінімумом (максимумом), якщо 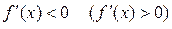 ліворуч від цієї точки і
ліворуч від цієї точки і 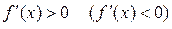 праворуч від цієї точки.
праворуч від цієї точки.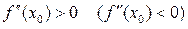 .
. і 2)
і 2) 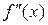 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 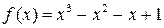 на екстремум.
на екстремум. Знаходимо похідну і прирівнюємо її нулю:
Знаходимо похідну і прирівнюємо її нулю:  . Отже, точками екстремуму є
. Отже, точками екстремуму є  і
і 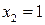 . Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції
. Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції 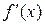 в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі (
в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі ( )
) 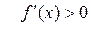 (функція
(функція 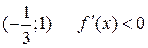 (функція
(функція 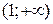
 (функція
(функція 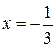 має локальний максимум
має локальний максимум 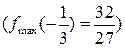 , а у точці х= 1 – локальний мінімум
, а у точці х= 1 – локальний мінімум  . Дійсно,
. Дійсно,  і
і  .
.




 x
x 1
1
 х
х . З
. З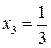 і, отже, дана точка є точкою перегину функції
і, отже, дана точка є точкою перегину функції 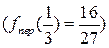 . Її графік наведено на Рис. 3.3.
. Її графік наведено на Рис. 3.3.




 4 у
4 у


 0
0 
 -2
-2

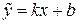 називається нахиленою асимптотою графіка функції
називається нахиленою асимптотою графіка функції 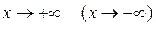 , де
, де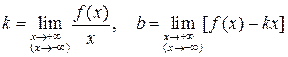 . (18)
. (18)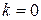 , тоді така асимптота називається горизонтальною
, тоді така асимптота називається горизонтальною  .
. (або
(або 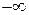 ).
). .
. і
і 
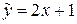 є нахиленою асимптотою графіка даної функції
є нахиленою асимптотою графіка даної функції  , так і при
, так і при  . Оскільки
. Оскільки 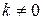 , то горизонтальних асимптот немає.
, то горизонтальних асимптот немає.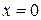 є точкою розриву даної функції
є точкою розриву даної функції 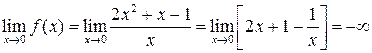 . Отже, пряма
. Отже, пряма 



 20
20
 у
у
 10
10


 0
0







 0 х
0 х

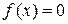 )
)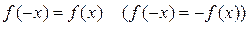 .
.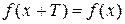 , де
, де 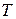 – період функції
– період функції 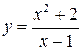 .
. (точка х = 1 є точкою розриву).
(точка х = 1 є точкою розриву).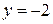 (при
(при 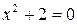 не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис.
не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис. . Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо:
. Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо: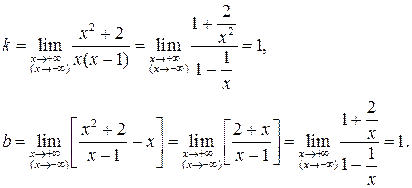
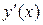 + max – – min +
+ max – – min +




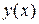
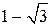 1
1  x
x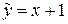 є нахилена асимптота даної функції. Горизонтальних асимптот немає.
є нахилена асимптота даної функції. Горизонтальних асимптот немає.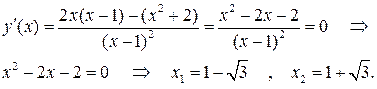
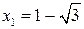 є точкою максимуму,
є точкою максимуму, 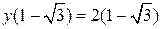 , а
, а 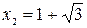 є точкою мінімуму,
є точкою мінімуму, 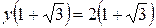 . Функція зростає на інтервалах
. Функція зростає на інтервалах 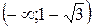 і
і  . Функція спадає на інтервалі
. Функція спадає на інтервалі  . З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну:
. З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну: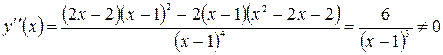 . Отже, точок перегину функція немає.
. Отже, точок перегину функція немає.



 40 y
40 y 30
30 20
20

 10
10  0
0


 0
0  1 x
1 x -20
-20




 -40
-40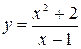
 , за яким кожній впорядкованій парі незалежних змінних
, за яким кожній впорядкованій парі незалежних змінних  ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці
ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці  . Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність
. Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність  (рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок
(рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок  .
. визначена у деякому околі точки
визначена у деякому околі точки  . Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку):
. Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку): 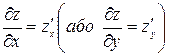 .
. .
. .
. .
. .
.

 .
. і
і  називаються мішаними частиннимипохідними.
називаються мішаними частиннимипохідними. зручно ввести поняття похідної за напрямком:
зручно ввести поняття похідної за напрямком: . (19)
. (19) у точці
у точці  за напрямком вектора
за напрямком вектора  , де А - точка з координатами
, де А - точка з координатами  .
. , який задає напрямок
, який задає напрямок  . Далі обчислимо частинні похідні функції z у точці
. Далі обчислимо частинні похідні функції z у точці  .
.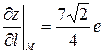 .
. . (20)
. (20)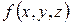 визначається за такою формулою:
визначається за такою формулою: .
.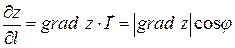 ,
, - кут між векторами
- кут між векторами  . Звідси випливає, що похідна функції за напрямком має найбільшу величину при
. Звідси випливає, що похідна функції за напрямком має найбільшу величину при 
 , тобто коли напрямок вектора
, тобто коли напрямок вектора  . Якщо
. Якщо  має в точці
має в точці  частинні похідні першого порядку, тоді в цій точці вони дорівнюють нулю (необхідна умова екстремуму):
частинні похідні першого порядку, тоді в цій точці вони дорівнюють нулю (необхідна умова екстремуму):
 (21)
(21)
 , тоді в точці
, тоді в точці  - локальний мінімум, а при
- локальний мінімум, а при 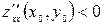 - локальний максимум;
- локальний максимум;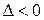 , тоді в точці
, тоді в точці 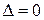 , тоді в точці
, тоді в точці 


