
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція двох змінних. Частинні похідні.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Градієнт функції. Нехай задано закон Приклад 1. Розглянемо функцію двох змінних Нехай функція Приклад 2. Знайти частинні похідні першого порядку від функції
Приклад 3. Знайти частинні похідні другого порядку від функції Для цього знайдемо спочатку частинні похідні першого порядку:
Далі отримуємо:
Зауваження. Похідні Для характеристики швидкості зміни функції в точці
Приклад 4. Обчислити похідну функції Спочатку знайдемо координати одиничного вектора
За формулою (19) маємо: Градієнтом функції
Зауваження. У просторі градієнт функції
З урахуванням виразу (20) формулу (19) можна переписати так
де Отже, градієнт функції Екстремум функції двох змінних. Метод найменших квадратів.
Нехай функція
Нехай у точці
Тоді (достатня умова екстремуму): 1). якщо 2). якщо 3). якщо Приклад 1. Дослідити на екстремум функцію Знаходимо точку можливого екстремуму:
Далі обчислюємо визначник (22): Приклад 2. Дослідити на екстремум функцію Маємо:
У точці Приклад 3. По розташованим на координатній площині п експериментальним точкам встановити вигляд функції Розглянемо, наприклад, лінійну інтерполяцію:
де Розглянемо суму квадратів похибок:
Таким чином, наша задача зводиться до знаходження таких коефіцієнтів
Отримана система (23) називається нормальною системою методу найменших квадратів. З цієї системи знаходимо коефіцієнти Нарешті, легко показати, що функція
Невизначений інтеграл
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 700; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.240 (0.007 с.) |

 , за яким кожній впорядкованій парі незалежних змінних
, за яким кожній впорядкованій парі незалежних змінних  ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці
ставиться у відповідність хоча б єдине число z. Число z називають значенням функції f у точці  . Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність
. Область визначення цієї функції - це множина усіх точок, які задовольняють нерівність  (рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок
(рівняння кола радіусом 1 з центром у початку координат). Множиною значень даної функції є відрізок  .
. визначена у деякому околі точки
визначена у деякому околі точки  . Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку):
. Тоді частинна похідна цієї функції за змінною x (або y) визначається як звичайна похідна функції однієї змінної x (або y) за фіксованого значення змінної y (або x) і позначається так (частинна похідна першого порядку): 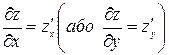 .
. .
. .
. .
. .
.

 .
. і
і  називаються мішаними частиннимипохідними.
називаються мішаними частиннимипохідними. зручно ввести поняття похідної за напрямком:
зручно ввести поняття похідної за напрямком: . (19)
. (19) у точці
у точці  за напрямком вектора
за напрямком вектора  , де А - точка з координатами
, де А - точка з координатами  .
. , який задає напрямок
, який задає напрямок  . Далі обчислимо частинні похідні функції z у точці
. Далі обчислимо частинні похідні функції z у точці  .
.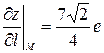 .
. . (20)
. (20)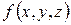 визначається за такою формулою:
визначається за такою формулою: .
.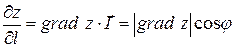 ,
, - кут між векторами
- кут між векторами  . Звідси випливає, що похідна функції за напрямком має найбільшу величину при
. Звідси випливає, що похідна функції за напрямком має найбільшу величину при 
 , тобто коли напрямок вектора
, тобто коли напрямок вектора  . Якщо
. Якщо  має в точці
має в точці  частинні похідні першого порядку, тоді в цій точці вони дорівнюють нулю (необхідна умова екстремуму):
частинні похідні першого порядку, тоді в цій точці вони дорівнюють нулю (необхідна умова екстремуму):
 (21)
(21)
 , тоді в точці
, тоді в точці  - локальний мінімум, а при
- локальний мінімум, а при 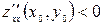 - локальний максимум;
- локальний максимум;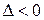 , тоді в точці
, тоді в точці 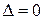 , тоді в точці
, тоді в точці 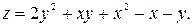
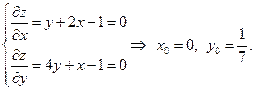
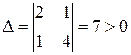 . Оскільки
. Оскільки 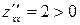 , тоді в точці
, тоді в точці 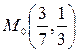 дана функція має локальний мінімум.
дана функція має локальний мінімум.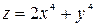 .
.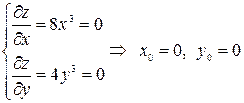 .
.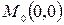
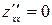 і
і 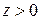 у всіх точках за винятком точки
у всіх точках за винятком точки 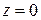 у точці
у точці 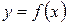 , яка б добре описувала ці експериментальні значення (задача інтерполяції).
, яка б добре описувала ці експериментальні значення (задача інтерполяції).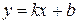 . Зрозуміло, що ця формула є наближеною. Тому, підставляючи значення координат експериментальних точок
. Зрозуміло, що ця формула є наближеною. Тому, підставляючи значення координат експериментальних точок 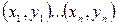 у цей вираз, отримуємо такі рівності
у цей вираз, отримуємо такі рівності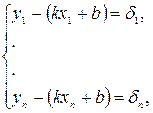
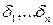 - деякі похибки (відхилення). Отже, задача полягає у тому, що необхідно підібрати такі коефіцієнти k і b, щоб похибки були якнайменшими за абсолютною величиною. Для цього використаємо метод найменших квадратів.
- деякі похибки (відхилення). Отже, задача полягає у тому, що необхідно підібрати такі коефіцієнти k і b, щоб похибки були якнайменшими за абсолютною величиною. Для цього використаємо метод найменших квадратів.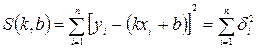 .
.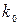 і
і 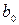 , за яких функція
, за яких функція 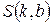 має мінімум:
має мінімум: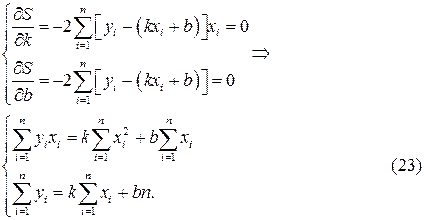
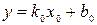 .
.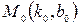 . Дійсно,
. Дійсно, 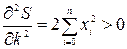 і
і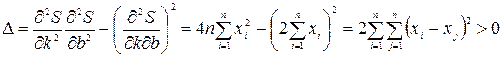 .
.


