
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання випадкових векторів і функційСодержание книги
Поиск на нашем сайте
Мета лабораторної роботи – познайомитись із методами моделювання випадкових векторів і функцій, отримати і закріпити практичні навички з використання алгоритмів методів моделювання випадкових векторів і функцій для розв'язання конкретних задач. Короткі теоретичні відомості Моделювання випадкових векторів. Нехай багатовимірна випадкова величина (випадковий вектор) зі складовими Хі(і=
У випадку залежних координат Хі складові випадкового вектора визначаються у процесі моделювання як лінійне перетворення некорельованих розподілених за нормальним законом нормованих випадкових величин {V1, V2, …, Vn,} Î N(0, 1), m = 0, σ = 1:
Коефіцієнти претворення послідовно визначають із співвідношень:
Моделювання випадкових функцій. Випадковою називається функція, ординати якої для будь-яких фіксованих значень аргумента є випадковими величинами. Задачу моделювання випадкових функцій у загальному випадку не можна звести до моделювання випадкової функції для кожного значення аргументу, оскільки між значеннями функції існує кореляційна залежність. Випадкова функція, аргументом якої є час (t) носить назву випадкового процесу. Для моделювання реалізацій нестаціонарних випадкових процесів використовують спосіб, заснований на методі канонічних розкладів. Суть методу полягає у тому, що реалізація випадкового процесу Х(t) на скінченому інтервалі часу задається у вигляді суми елементарних випадкових функцій
Тут Wk – центровані некоректовані випадкові величини з дисперсіями Dk i математичним сподіванням m=0, а fk – невипадкові координатні функції часу. Якщо канонічний розклад випадкового процесу є відомим, то його кореляційна функція має вигляд
Дисперсія визначається за формулою
Невипадкові координатні функції часу fk для усіх значень функції на інтервалі, що розглядається, а також дисперсії випадкових величин визначається за співвідношеннями:
Зазначимо, що якщо i > j, то fi(tj) = 0, а також fi(tі) = 1. Таким чином, алгоритм моделювання реалізацій нестаціонарного випадкового процесу, що задається математичним сподіванням mx(t) і кореляційною функцією Kx(ti, tj) є таким
· За вхідними даними процесу для всіх дискретних значень функцій у моменти часу tj · Із сукупності випадкових чисел вибирають n чисел і перетворюють їх будь-яким відомим способом у випадкові величини W з заданим розподілом (mW = 0, DW = D). Значення випадкового процесу визначають згідно з виразами:
Наведений алгоритм моделювання у випадку стаціонарних випадкових процесів суттєво спрощується, оскільки у цьому випадку кореляційна функція Постановка завдання Відповідно до заданого варіанта: 1. Отримати послідовність реалізацій випадкового вектора заданого обсягу (значень випадкової функції на заданому інтервалі часу). 2. Побудувати графік зміни реалізації випадкової функції та координатних функцій канонічного розкладу на заданому інтервалі часу. 3. Записати кількість реалізацій розподілів випадкового вектора. Індивідуальні завдання для моделювання Варіант 1 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 2 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 3 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 4 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки. Варіант 5 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с.
Варіант 6 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Варіант 7 Змоделювати N = 10 реалізацій тривимірного випадкового вектора з математичним сподіванням
Варіант 8 Бортова система автоматичного управління ПС в режимі автоматичного заходу на посадку здійснює вихід літака на висоту прийняття рішення. Відхилення літака від рівносигнальних зон курсу і глісади в момент прольоту ВПР описується нормальним законом розподілу з параметрами: mx=0, тy= 0, σx = 3, σy = 2, kxy = 1.5. Змоделювати N = 20 реалізацій процесу заходу на посадку. Варіант 9 Проводиться стрільба по точковій цілі на площині. Розсіяння точки розриву снаряду проходить за нормальним законом, центр якого співпадає з ціллю (тх = ту = 0), а кореляційна матриця має вигляд:
Попадання в ціль відбувається, якщо відстань від неї до точки розриву снаряда не перевищує r0 = 10м. Змоделювати результати N = 10 пострілів і визначити кількість попадань. Варіант 10 Похибка автоматичної системи спостереження описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 0.01t і кореляційною функцією k(t, t+τ) = 1.2e-ατ cos βτ, де α = 0.05; β = 0.04. Отримати канонічний розклад випадкової функції і змоделювати реалізацію похибки на інтервалі [0, 100]с, з кроком дискретності τ = 10 с. Варіант 11 Частота обертання валу електродвигуна змінюється під впливом випадкових коливань напруги живлення і навантаження на валу і описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 3*103 sin0.2 t і кореляційною функцією k(t,t + τ) = Dt * е-ατ, де Dt = 20.5 t; α= 0.05. Отримати канонічний розклад випадкової функції і змоделювати реалізацію частоти обертання валу електродвигуна на інтервалі [0; 40] с, з кроком дискретності τ = 4 с. Варіант 12 Динамічна похибка систем автоматичної зміни частоти є нестаціонарний випадковий процес з нульовим математичним сподіванням і кореляційною функцією k(t,t + τ) = Dt * е-ατ cosβτ; Dt = 200 + 5 t; α =0.2; β =0.5. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію динамічної похибки системи на інтервалі [0; 20] с, з кроком дискретності τ = 2 с. Варіант 13 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 14 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 15 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 16 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки.
Варіант 17 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с. Варіант 18 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Варіант 19 Змоделювати N = 10 реалізацій тривимірного випадкового вектора з математичним сподіванням
Варіант 20 Бортова система автоматичного управління ПС в режимі автоматичного заходу на посадку здійснює вихід літака на висоту прийняття рішення. Відхилення літака від рівносигнальних зон курсу і глісади в момент прольоту ВПР описується нормальним законом розподілу з параметрами: mx=0, тy= 0, σx = 3, σy = 2, kxy = 1.5. Змоделювати N = 20 реалізацій процесу заходу на посадку. Варіант 21 Проводиться стрільба по точковій цілі на площині. Розсіяння точки розриву снаряду проходить за нормальним законом, центр якого співпадає з ціллю (тх = ту = 0), а кореляційна матриця має вигляд:
Попадання в ціль відбувається, якщо відстань від неї до точки розриву снаряда не перевищує r0 = 10м. Змоделювати результати N = 10 пострілів і визначити кількість попадань. Варіант 22 Похибка автоматичної системи спостереження описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 0.01t і кореляційною функцією k(t, t+τ) = 1.2e-ατ cos βτ, де α = 0.05; β = 0.04. Отримати канонічний розклад випадкової функції і змоделювати реалізацію похибки на інтервалі [0, 100]с, з кроком дискретності τ = 10 с. Варіант 23 Частота обертання валу електродвигуна змінюється під впливом випадкових коливань напруги живлення і навантаження на валу і описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 3*103 sin0.2 t і кореляційною функцією k(t,t + τ) = Dt * е-ατ, де Dt = 20.5 t; α= 0.05. Отримати канонічний розклад випадкової функції і змоделювати реалізацію частоти обертання валу електродвигуна на інтервалі [0; 40] с, з кроком дискретності τ = 4 с.
Варіант 24 Динамічна похибка систем автоматичної зміни частоти є нестаціонарний випадковий процес з нульовим математичним сподіванням і кореляційною функцією k(t,t + τ) = Dt * е-ατ cosβτ; Dt = 200 + 5 t; α =0.2; β =0.5. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію динамічної похибки системи на інтервалі [0; 20] с, з кроком дискретності τ = 2 с. Варіант 25 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 26 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 27 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 28 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки. Варіант 29 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с. Варіант 30 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Лабораторна робота 4
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.007 с.) |

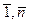 ) задається математичними сподіваннями mi = M [Xi] і матрицею кореляційних моментів:
) задається математичними сподіваннями mi = M [Xi] і матрицею кореляційних моментів: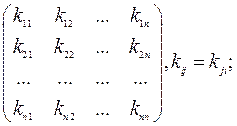
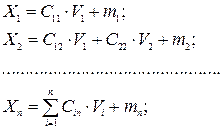
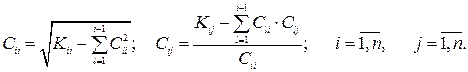
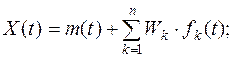
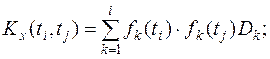
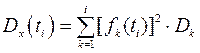 .
.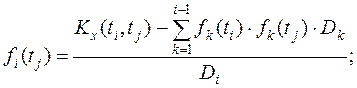
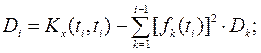
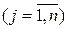 визначають дисперсії Di і координатні функції канонічного розкладу fi(tj).
визначають дисперсії Di і координатні функції канонічного розкладу fi(tj).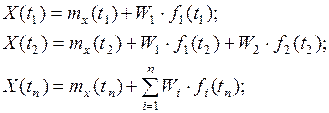
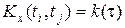 не залежить від вибору аргументів, а визначається лише їх різницею
не залежить від вибору аргументів, а визначається лише їх різницею 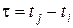 .
.
 = (0,0,0) та кореляційною матрицею
= (0,0,0) та кореляційною матрицею
 з математичним сподіванням
з математичним сподіванням 







