
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання неперервних випадкових величинСодержание книги
Поиск на нашем сайте
Мета лабораторної роботи – познайомитись із методами моделювання неперервних випадкових величин, отримати і закріпити практичні навички з використання цих. Короткі теоретичні відомості Серед існуючих методів моделювання неперервних випадкових величин з довільним законом розподілу на основі випадкових чисел з рівномірним розподілом в інтервалі [0, 1] розглянемо методи оберненої функції. Суть методу полягає у тому, що значення випадкової величини хі з функцією розподілу F(x) можемо отримати з рівняння F(xі) = rі, де rі – випадкові числа рівномірно розподілені в інтервалі [0,1]. Тоді значення xі випадкової величини отримується як розв’язок рівняння X = F-1 (r), де F-1 – обернена функція у відношенні до F. Таким чином, щоразу, коли необхідно отримати визначене значення випадкових величин х1, х2, …, хn із заданою функцією щільності розподілу f(x) то генеруємо випадкове число
Розглянемо на прикладі застосування методу оберненої функції. Змоделюємо неперервну випадкову величину, розподілену за експоненціальним законом розподілу. Його функція щільності має вигляд:
Згідно методу оберненої функції отримаємо
Звідси знаходимо
Можна показати, що випадкові величини (1-ri) та ri мають один і той же розподіл. Тоді можемо знайти:
Постановка завдання Відповідно до заданого варіанту: 1. Знайти послідовність М = 100 реалізацій неперервної випадкової величини за порядком їх появи. 2. Побудувати гістограму f * (х) модельованої величини. Індивідуальні завдання для моделювання Варіант 1 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 1, λ = 3. Варіант 2 Неперервна випадкова величина має рівномірний розподіл в інтервалі [5, 10]. Варіант 3 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 2, σ = 3. Варіант 4 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,4. Варіант 5 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-1, 1]. Варіант 6 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 10, σ = 5. Варіант 7 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,9.
Варіант 8 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,5. Варіант 9 Неперервна випадкова величина має рівномірний розподіл в інтервалі [1, 10]. Варіант 10 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,7. Варіант 11 Неперервна випадкова величина має рівномірний розподіл в інтервалі [1, 2]. Варіант 12 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,3. Варіант 13 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 2, λ = 3. Варіант 14 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,2. Варіант 15 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т= 0, σ = 2. Варіант 16 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 3, λ = 2. Варіант 17 Неперервна випадкова величина має рівномірний розподіл в інтервалі [2, 6]. Варіант 18 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 5, σ = 2. Варіант 19 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,2. Варіант 20 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-5, -2]. Варіант 21 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 4, σ = 3. Варіант 22 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 2,9. Варіант 23 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,5. Варіант 24 Неперервна випадкова величина має рівномірний розподіл в інтервалі [7, 12]. Варіант 25 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,6. Варіант 26 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-10, -5]. Варіант 27 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 4,2. Варіант 28 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 1, λ = 5. Варіант 29 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,4.
Варіант 30 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т= 10, σ = 3.
Лабораторна робота 3
|
||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.88.161 (0.008 с.) |

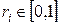 та обчислюємо значення, яке є розв’язком рівняння
та обчислюємо значення, яке є розв’язком рівняння
 .
.

 .
.


