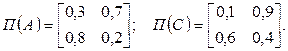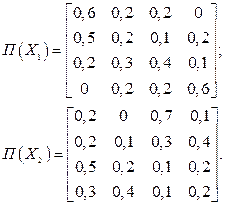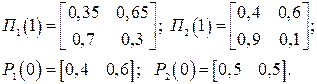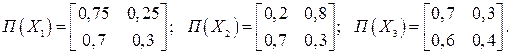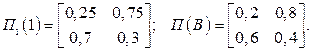Моделювання дискретних систем

Мета лабораторної роботи – ознайомитись з алгоритмами моделювання дискретних систем та отримати практичні навички з моделювання ланцюгів Маркова та імовірнісних автоматів.

Короткі теоретичні відомості

Домовимося позначати через S_і(k) подію того, що після k кроків система знаходиться у стані S_і. Процес, який відбувається у системі, можна представити як послідовність подій:

S₁(k), S₂(k), S₃(k), S₄(k), …,

яка називається марківським ланцюгом.

Позначимо ймовірність переходу (або перехідну ймовірність) системи зі стану S_і → S_j за один крок P_ij(k), тобто

де S_і(k), S_і(k-1) – стан системи у моменти часу t_k i t_k-1, тобто на k -у і (k-1)- у кроці.

Ймовірності P_ij(k) є основними характеристиками марківського процесу.

Якщо P_ij(k) = P_ij - то марківський процес називається однорідним (тобто ймовірності не залежить від кроку переходу систем).

Тоді

.

Розглянемо однорідні марківські процеси.

Нехай процес починається зі стану S_і. Яка ймовірність того, що через m кроків процес перейде у стан S_j. Така ймовірність визначається рівнянням Кампорова-Чемпона

де 1 ≤ s ≤ m.

Якщо відомо матрицю перехідних ймовірностей (або розміщений граф станів) і початковий розподіл (у момент часу t = 0) ймовірностей для усіх станів , можна знайти ймовірності станів для будь-якого кроку за формулою:

де - ймовірність переходу системи зі стану S_j → S_i за k кроків.

Постановка завдання

Відповідно до заданого варіанта отримати послідовність вхідних сигналів, станів та вихідних сигналів на кожному з кроків.

Індивідуальні завдання для моделювання

Варіант 1

Спеціалізована операційна система приймає в обробку три класи завдань А, В і С з різним необхідним обсягом оперативної пам'яті. Імовірності появи завдань Р(А) = 0.5; Р(В) = 0.3; Р(С) = 0.2. В момент надходження завдання система може знаходитися в одному з двох станів: z₁ – має вільні ресурси і може прийняти додаткові завдання; z₂ – монополізована попередніми завданнями. Матриці перехідних імовірностей системи такі:

Вихідний сигнал – це стан системи в момент надходження чергового завдання. Змоделювати роботу ОС при надходженні k = 20 завдань, якщо функціонування системи починається за відсутності завдань.

Варіант 2

Ремонтний цех АТБ, що включає в себе декілька ліній, здійснює обслуговування блоків АО з різним ступенем пошкодження. Можливі пошкодження трьох типів: А, В і С, імовірності появи яких Р(А) = 0,5; Р(В) = 0,15; Р(С) = 0,35. Блоки надходять у цех в дискретні моменти часу. Можливі стани цеху: z₁ – є хоча б одна лінія, на яку надходить блок; z₂ – всі лінії зайняті. Матриці перехідних імовірностей станів цеху:

Змоделювати роботу цеху з обслуговування к = 18 блоків, якщо в початковий момент всі лінії цеху вільні.

Варіант 3

Система передачі даних має два незалежні канали. Через кожні 30 с надходять повідомлення для передачі. Кожний із каналів може знаходитися в одному з двох станів: z₁ – вільний; z₂ – зайнятий передачею повідомлення. Матриці перехідних імовірностей і початкових імовірностей першого і другого каналів відповідно мають вигляд:

Змоделювати стани системи передачі за 10 хв.

Варіант 4

Процесор автоматизованої інформаційної системи може перебувати в одному зі станів:

z₁ - обробка інформації;

z₂ - простій через несправність процесора;

z₃ - простій через відсутність інформації.

Контроль станів системи здійснюється через кожні 15 хв. Якщо виявлена несправність фахівці приступають до ремонту. Матриця початкових імовірностей станів системи має вигляд:

Р(0) = (0,5 0,4 0,1),

а матриця умовних перехідних імовірностей:

Змоделювати процес роботи системи за 5 год.

Варіант 5

Електронний блок експлуатується в одному з таких режимів: Х₁,Х₂,Х₃, імовірності виникнення яких відповідно Р(Х_]) = 0.5; Р(Х₂) = 0.3; Р(Х₃) = 0.2. Інтенсивність відмов блоку залежить від режиму роботи. Стани блоку: z₁ – справний; z₂ – несправний. У випадку відмови блок відновлюється. Змоделювати стани блоку в дискретні моменти контролю t_k, t= 1,2,...,20. Якщо в початковий момент роботи блок справний, а матриці перехідних імовірностей:

Варіант 6

Точка А „блукає” по осі абсцис відповідно до закону: на кожному кроці вона з імовірністю 0,5 залишається на місці, з імовірністю 0,3 зміщується на одиницю вправо і з імовірністю 0,2 – вліво.

Промоделювати реалізацію переходів і визначити кінцевий стан точки А за k = 20 кроків, якщо її початковий стан – початок координат.

Варіант 7

Тригер може знаходитися в одному з двох стійких станів: z₁ = 0 і z₂ = 1. Сукупність вхідних сигналів надходить у дискретні моменти часу t₁, t₂,... і приймає дві різні комбінації значень, які кодуються X₁ і Х₂, і переводять тригер з одного стану в інший. Тригер функціонує в стохастичних умовах під дією внутрішніх і зовнішніх випадкових збурень. Імовірності вхідних сигналів: Р(Х₁) = 0.55; Р(Х₂) = 0.45, матриці перехідних імовірностей:

Змоделювати переходи станів тригера за k = 20 тактів, якщо його початкові стани рівномірні.

Варіант 8

ОС включає в себе два процесори. Завдання на обробку надходять кожні 30 хв. і залежно від складності займають один або два процесори. Система може знаходитись в станах: z₁ – справні два процесори; z₂ – справний перший процесор; z₃ – справний другий процесор; z₄ – обидва процесори несправні. Процесор, що вийшов з ладу, відновлюється. Змоделювати стан системи протягом 10 год, якщо в початковий момент два процесори справні, а матриці перехідних імовірностей кожного процесора мають вигляд:

Варіант 9

Двоканальна інформаційна система функціонує при різних рівнях сигналу, які змінюються стрибкоподібно і можуть бути віднесені до одного з двох класів А і В, що не перетинаються. В кожний момент контролю t_k, k = 1,2,... система може знаходитися в одному зі станів: z₁ – обидва канали в робочому стані; z₂ – один канал несправний; z₃ – система вийшла з ладу. Відомі імовірності появи сигналів: Р(А) = 0.7, Р(В) = 0.3, а також матриці перехідних ймовірностей системи:

Змоделювати стани системи за k = 15 тактів контролю, якщо на початку працездатні обидва канали.

Варіант 10

Інформаційна система, яка складається з т = 2 незалежних об'єктів, кожні 15 хв. піддається контролю. Кожний із об'єктів системи може знаходитись в одному з двох станів: z₁ – справний; z₂ – несправний. Матриці перехідних імовірностей об'єктів контролю мають вигляд:

Змоделювати зміни станів системи за 5 год, якщо в початковий момент (t = 0) обидва об'єкти справні.

Варіант 11

Автоматична технологічна лінія, що здійснює випуск пристроїв для ЕОМ, підлягає огляду в моменти часу t_i (і = 1,2,..., n).

Можливі стани лінії:

z₁ – повністю справна;

z₂ – порушення технологічного процесу (брак);

z₃ – простій лінії (відсутні комплектуючі виробу);

z₄ – лінія вийшла з ладу.

Матриця імовірностей початкових станів має вигляд:

Р(0) = [0,7 0,1 0,2 0],

а матриця перехідних імовірностей:

Варіант 12

Змоделювати процес функціонування імовірнісного автомата з випадковими переходами за k = 20 тактів, якщо його вхідний алфавіт двійковий X = {х₁, х₂}, множини станів автомата Z і вихідний алфавіт Y трійкові z = {z₁,z₂, z₃}, у = {у₁, у₂, у₃} Матриця переходів станів автомата має вигляд:

Початковий стан z₀ і вхідний сигнал X автомата задані розподілами: Р_z (0) = [ Pzo₁ = 0,7 Pzo₂ = 0.3 Pzo₃ = 0]; Р_х (0) = [ Рх₁ = 0.5 Рх₂ = 0.5]. Функція виходів автомата детермінована і задає вихідний сигнал у_i(t_k) = z_i{t_k).

Варіант 13

Для функціонування блока інформаційної системи достатньо, щоб працював хоча б один із двох взаємозамінюваних вузлів. При виході з ладу одного із вузлів блок продовжує нормально функціонувати за рахунок іншого. Контроль станів блока здійснюється через кожні 20 хв роботи. Вузол, що вийшов з ладу, починає ремонтуватись. Матриця перехідних імовірностей станів блока має вигляд:

Змоделювати процес функціонування блока за 5 год., якщо в початковий момент (t = 0) обидва вузли справні.

Варіант 14

На складі зберігаються і видаються для проведення ремонту інформаційно-обчислювальної техніки запасні частини. Замовлення на видачу комплектів надходять через 2 год. У процесі роботи склад може знаходитися в одному зі станів: z₁ – наявні всі необхідні комплекти; z₂ – видаються деякі з необхідних комплектів; z₃ – необхідні комплекти відсутні. Змоделювати процес роботи складу протягом 40 год, якщо матриці перехідних П(1) і початкових Р(0) імовірностей мають вигляд:

Варіант 15

Інформаційна система в дискретні моменти часу під впливом двійкового вхідного сигналу X = { 0; 1 } і внутрішніх випадкових факторів змінює свій стан на множині Z = { z₁ z₂ z₃ z₄ }. Відомі дискретні розподіли імовірностей вхідного сигналу Р_х і початкового стану системи P_z(0):

Р_х= [ 0,65 0,35]; P_z(0) = [ 0,3 0,2 0,4 0,1 ],

а також матриці перехідних імовірностей:

Змоделювати процес зміни станів системи за k = 20 тактів контролю.

Варіант 16

Спеціалізована операційна система приймає в обробку три класи завдань А, В і С з різним необхідним обсягом оперативної пам'яті. Імовірності появи завдань Р(А) = 0.45; Р(В) = 0.4; Р(С) = 0.15. В момент надходження завдання система може знаходитися в одному з двох станів: z₁ – має вільні ресурси і може прийняти додаткові завдання; z₂ – монополізована попередніми завданнями. Матриці перехідних імовірностей системи такі:

Вихідний сигнал – це стан системи в момент надходження чергового завдання. Змоделювати роботу ОС при надходженні k = 25 завдань, якщо функціонування системи починається за відсутності завдань.

Варіант 17

Ремонтний цех АТБ, що включає в себе декілька ліній, здійснює обслуговування блоків АО з різним ступенем пошкодження. Можливі пошкодження трьох типів: А, В і С, імовірності появи яких Р(А) = 0,4; Р(В) = 0,35; Р(С) = 0,25. Блоки надходять у цех в дискретні моменти часу. Можливі стани цеху: z₁ – є хоча б одна лінія, на яку надходить блок; z₂ – всі лінії зайняті. Матриці перехідних імовірностей станів цеху:

Змоделювати роботу цеху з обслуговування к = 20 блоків, якщо в початковий момент всі лінії цеху вільні.

Варіант 18

Система передачі даних має два незалежні канали. Через кожні 30 с надходять повідомлення для передачі. Кожний із каналів може знаходитися в одному з двох станів: z₁ – вільний; z₂ – зайнятий передачею повідомлення. Матриці перехідних імовірностей і початкових імовірностей першого і другого каналів відповідно мають вигляд:

Змоделювати стани системи передачі за 10 хв.

Варіант 19

Процесор автоматизованої інформаційної системи може перебувати в одному зі станів:

z₁ - обробка інформації;

z₂ - простій через несправність процесора;

z₃ - простій через відсутність інформації.

Контроль станів системи здійснюється через кожні 15 хв. Якщо виявлена несправність фахівці приступають до ремонту. Матриця початкових імовірностей станів системи має вигляд:

Р(0) = (0,3 0,2 0,5),

а матриця умовних перехідних імовірностей:

Змоделювати процес роботи системи за 5 год.

Варіант 20

Електронний блок експлуатується в одному з таких режимів: Х₁,Х₂,Х₃, імовірності виникнення яких відповідно Р(Х_]) = 0.5; Р(Х₂) = 0.2; Р(Х₃) = 0.3. Інтенсивність відмов блоку залежить від режиму роботи. Стани блоку: z₁ – справний; z₂ – несправний. У випадку відмови блок відновлюється. Змоделювати стани блоку в дискретні моменти контролю t_k, t= 1,2,...,20. Якщо в початковий момент роботи блок справний, а матриці перехідних імовірностей:

Варіант 21

Точка А „блукає” по осі абсцис відповідно до закону: на кожному кроці вона з імовірністю 0,4 залишається на місці, з імовірністю 0,25 зміщується на одиницю вправо і з імовірністю 0,35 – вліво.

Промоделювати реалізацію переходів і визначити кінцевий стан точки А за k = 25 кроків, якщо її початковий стан – початок координат.

Варіант 22

Тригер може знаходитися в одному з двох стійких станів: z₁ = 0 і z₂ = 1. Сукупність вхідних сигналів надходить у дискретні моменти часу t₁, t₂,... і приймає дві різні комбінації значень, які кодуються X₁ і Х₂, і переводять тригер з одного стану в інший. Тригер функціонує в стохастичних умовах під дією внутрішніх і зовнішніх випадкових збурень. Імовірності вхідних сигналів: Р(Х₁) = 0.35; Р(Х₂) = 0.65, матриці перехідних імовірностей:

Змоделювати переходи станів тригера за k = 20 тактів, якщо його початкові стани рівномірні.

 

Варіант 23

ОС включає в себе два процесори. Завдання на обробку надходять кожні 30 хв. і залежно від складності займають один або два процесори. Система може знаходитись в станах: z₁ – справні два процесори; z₂ – справний перший процесор; z₃ – справний другий процесор; z₄ – обидва процесори несправні. Процесор, що вийшов з ладу, відновлюється. Змоделювати стан системи протягом 10 год, якщо в початковий момент два процесори справні, а матриці перехідних імовірностей кожного процесора мають вигляд:

Варіант 24

Двоканальна інформаційна система функціонує при різних рівнях сигналу, які змінюються стрибкоподібно і можуть бути віднесені до одного з двох класів А і В, що не перетинаються. В кожний момент контролю t_k, k = 1,2,... система може знаходитися в одному зі станів: z₁ – обидва канали в робочому стані; z₂ – один канал несправний; z₃ – система вийшла з ладу. Відомі імовірності появи сигналів: Р(А) = 0.6, Р(В) = 0.4, а також матриці перехідних ймовірностей системи:

Змоделювати стани системи за k = 15 тактів контролю, якщо на початку працездатні обидва канали.

Варіант 25

Інформаційна система, яка складається з т = 2 незалежних об'єктів, кожні 15 хв. піддається контролю. Кожний із об'єктів системи може знаходитись в одному з двох станів: z₁ – справний; z₂ – несправний. Матриці перехідних імовірностей об'єктів контролю мають вигляд:

Змоделювати зміни станів системи за 5 год, якщо в початковий момент (t = 0) обидва об'єкти справні.

Варіант 26

Автоматична технологічна лінія, що здійснює випуск пристроїв для ЕОМ, підлягає огляду в моменти часу t_i (і = 1,2,..., n).

Можливі стани лінії:

z₁ – повністю справна;

z₂ – порушення технологічного процесу (брак);

z₃ – простій лінії (відсутні комплектуючі виробу);

z₄ – лінія вийшла з ладу.

Матриця імовірностей початкових станів має вигляд:

Р(0) = [0,6 0,3 0,1 0],

а матриця перехідних імовірностей:

Варіант 27

Змоделювати процес функціонування імовірнісного автомата з випадковими переходами за k = 25 тактів, якщо його вхідний алфавіт двійковий X = {х₁, х₂}, множини станів автомата Z і вихідний алфавіт Y трійкові z = {z₁,z₂, z₃}, у = {у₁, у₂, у₃} Матриця переходів станів автомата має вигляд:

Початковий стан z₀ і вхідний сигнал X автомата задані розподілами: Р_z (0) = [ Pzo₁ = 0,6 Pzo₂ = 0.4 Pzo₃ = 0]; Р_х (0) = [ Рх₁ = 0.3 Рх₂ = 0.7]. Функція виходів автомата детермінована і задає вихідний сигнал у_i(t_k) = z_i{t_k).

Варіант 28

Для функціонування блока інформаційної системи достатньо, щоб працював хоча б один із двох взаємозамінюваних вузлів. При виході з ладу одного із вузлів блок продовжує нормально функціонувати за рахунок іншого. Контроль станів блока здійснюється через кожні 20 хв роботи. Вузол, що вийшов з ладу, починає ремонтуватись. Матриця перехідних імовірностей станів блока має вигляд:

Змоделювати процес функціонування блока за 5 год., якщо в початковий момент (t = 0) обидва вузли справні.

Варіант 29

На складі зберігаються і видаються для проведення ремонту інформаційно-обчислювальної техніки запасні частини. Замовлення на видачу комплектів надходять через 2 год. У процесі роботи склад може знаходитися в одному зі станів: z₁ – наявні всі необхідні комплекти; z₂ – видаються деякі з необхідних комплектів; z₃ – необхідні комплекти відсутні. Змоделювати процес роботи складу протягом 40 год, якщо матриці перехідних П(1) і початкових Р(0) імовірностей мають вигляд:

Варіант 30

Інформаційна система в дискретні моменти часу під впливом двійкового вхідного сигналу X = { 0; 1 } і внутрішніх випадкових факторів змінює свій стан на множині Z = { z₁ z₂ z₃ z₄ }. Відомі дискретні розподіли імовірностей вхідного сигналу Р_х і початкового стану системи P_z(0):

Р_х=[0,65 0,35]; P_z(0) = [ 0,3 0,4 0,2 0,1 ],

а також матриці перехідних імовірностей:

Змоделювати процес зміни станів системи за k = 25 тактів контролю.

 

Лабораторна робота 5