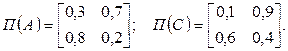Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання випадкових подій і дискретних випадкових величинСодержание книги
Поиск на нашем сайте
Лабораторна робота 1 Моделювання випадкових подій і дискретних випадкових величин Мета лабораторної роботи – познайомитись із методами моделювання простих, складних незалежних і залежних подій, а також дискретних випадкових величин, закріпити навички з побудови алгоритмів і програм реалізації цих методів. Короткі теоретичні відомості Змоделюємо настання деякої елементарної події А, ймовірність якої в одному випробуванні дорівнює Р(А)=Р. Нехай ri – рівномірно розподілені на інтервалі [0,1] величини, визначені генератором випадкових чисел. Подія А наступить тоді коли Нехай необхідно дослідити настання групи несумісних подій А1,А2,...,Ак, якщо відомі ймовірності їх настання Р(А1), Р(А2),...,Р(Ак). Попадання в інтервал від Моделювання сумісних залежних подій, наприклад, А і В, що мають імовірності настання РА і РB, полягає в наступному. Вважають, що одна з умовних імовірностей, наприклад, умовна імовірність настання події В при умові, що подія А відбулася Р(В/А), задана. Визначають імовірність можливих подій
отримаємо:
Отримаємо модель випадкової дискретної величини Таблиця 1.1
Випадкова величина приймає n значень
Якщо випадкову величину Постановка завдання Відповідно до заданого варіанту: Знайти послідовність М = 100 реалізацій випадкової події або дискретної випадкової величини за порядком їх появи. Індивідуальні завдання для моделювання Варіант 1 1. Складна подія, що складається з трьох незалежних простих подій А1, А2, А3 з імовірностями Р1 = 0,3; Р2 = 0,6, Р3 = 0,1. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 10 з однаковою імовірністю Р = 0,1. Варіант 2 1. Проста подія А з імовірністю появи Р = 0,6. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 3 1. Проста подія А з імовірністю появи Р = 0,7. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 4 1. Група k = 3 несумісних подій з імовірностями:
2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,6; N =10. Варіант 5 1. Складна подія, що складається з двох залежних подій A і В з імовірностями РА = 0,6; РB = 0,3; РB/Ā=0,7. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 5 з однаковою імовірністю Р = 0,2. Варіант 6 1. Проста подія А з імовірністю появи Р = 0,8. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 7 1. Складна подія, що складається з двох незалежних подій A і В з імовірностями РА = 0,8; РB =0,7. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 8 1. Група неcумісних подій k = 4 з імовірностями:
2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,5; N = 10. Варіант 9 1.Складна подія, що складається з двох залежних подій А і В з імовірностями РА = 0,8; РB = 0,5; РB/А =0,9. 2.Дискретна випадкова величина приймає значення з імовірностями відповідно:
Варіант 10 1. Проста подія А з імовірністю появи Р = 0,8. 2. Дискретна випадкова величина приймає значення з імовірностями відповіднo:
Варіант 11 1. Проста подія А з імовірністю Р = 0,7. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 4 з однаковою імовірністю Р = 0,25. Варіант 12 1. Складна подія, що складається з двох незалежних подій А і В з імовірностями появи РА = 0,5, РB = 0,8. 2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,75; N = 10. Варіант 13 1. Складна подія, що складається з трьох незалежних простих подій A1, А2, А3 з імовірностями P1 = 0,6, P2 = 0,2, Р3 = 0,4. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 14 1.Проста подія А з імовірністю Р = 0,25. 2.Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 15 1. Складна подія, що складається з двох залежних подій А і В з імовірностями РА = 0,6; РB = 0,4; PB/Ā=0,7. 2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,8; N = 10. Варіант 16 1. Складна подія, що складається з трьох незалежних простих подій А1, А2, А3 з імовірностями Р1 = 0,2; Р2 = 0,65, Р3 = 0,25. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 10 з однаковою імовірністю Р = 0,1. Варіант 17 1. Проста подія А з імовірністю появи Р = 0,45. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 18 1. Проста подія А з імовірністю появи Р = 0,5. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 19 1. Група k = 3 несумісних подій з імовірностями:
2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,4; N =10. Варіант 20 1. Складна подія, що складається з двох залежних подій A і В з імовірностями РА = 0,5; РB = 0,35; РB/Ā=0,6. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 5 з однаковою імовірністю Р = 0,2. Варіант 21 1. Проста подія А з імовірністю появи Р = 0,7. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 22 1. Складна подія, що складається з двох незалежних подій A і В з імовірностями РА = 0,7; РB =0,6. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 23 1. Група неcумісних подій k = 4 з імовірностями:
2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,6; N = 10. Варіант 24 1.Складна подія, що складається з двох залежних подій А і В з імовірностями РА = 0,5; РB = 0,7; РB/А =0,8. 2.Дискретна випадкова величина приймає значення з імовірностями відповідно:
Варіант 25 1. Проста подія А з імовірністю появи Р = 0,4. 2. Дискретна випадкова величина приймає значення з імовірностями відповіднo:
Варіант 26 1. Проста подія А з імовірністю Р = 0,45. 2. Дискретна випадкова величина приймає значення х 1, х 2,..., х 4 з однаковою імовірністю Р = 0,25. Варіант 27 1. Складна подія, що складається з двох незалежних подій А і В з імовірностями появи РА = 0,3, РB = 0,65. 2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,55; N = 10. Варіант 28 1. Складна подія, що складається з трьох незалежних простих подій A1, А2, А3 з імовірностями P1 = 0,4, P2 = 0,3, Р3 = 0,2. 2. Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 29 1.Проста подія А з імовірністю Р = 0,35. 2.Дискретна випадкова величина приймає значення з відповідними імовірностями:
Варіант 30 1. Складна подія, що складається з двох залежних подій А і В з імовірностями РА = 0,5; РB = 0,6; PB/Ā=0,3. 2. Дискретна випадкова величина має біноміальний розподіл з параметрами: Р = 0,7; N = 10. Лабораторна робота 2 Постановка завдання Відповідно до заданого варіанту: 1. Знайти послідовність М = 100 реалізацій неперервної випадкової величини за порядком їх появи. 2. Побудувати гістограму f * (х) модельованої величини. Індивідуальні завдання для моделювання Варіант 1 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 1, λ = 3. Варіант 2 Неперервна випадкова величина має рівномірний розподіл в інтервалі [5, 10]. Варіант 3 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 2, σ = 3. Варіант 4 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,4. Варіант 5 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-1, 1]. Варіант 6 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 10, σ = 5. Варіант 7 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,9. Варіант 8 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,5. Варіант 9 Неперервна випадкова величина має рівномірний розподіл в інтервалі [1, 10]. Варіант 10 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,7. Варіант 11 Неперервна випадкова величина має рівномірний розподіл в інтервалі [1, 2]. Варіант 12 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,3. Варіант 13 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 2, λ = 3. Варіант 14 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,2. Варіант 15 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т= 0, σ = 2. Варіант 16 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 3, λ = 2. Варіант 17 Неперервна випадкова величина має рівномірний розподіл в інтервалі [2, 6]. Варіант 18 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 5, σ = 2. Варіант 19 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,2. Варіант 20 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-5, -2]. Варіант 21 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т = 4, σ = 3. Варіант 22 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 2,9. Варіант 23 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,5. Варіант 24 Неперервна випадкова величина має рівномірний розподіл в інтервалі [7, 12]. Варіант 25 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 1,6. Варіант 26 Неперервна випадкова величина має рівномірний розподіл в інтервалі [-10, -5]. Варіант 27 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 4,2. Варіант 28 Неперервна випадкова величина має розподіл Вейбула з параметрами а = 1, λ = 5. Варіант 29 Неперервна випадкова величина має експоненціальний розподіл з параметром λ = 0,4. Варіант 30 Неперервна випадкова величина має нормальний розподіл N(m,σ) з параметрами т= 10, σ = 3.
Лабораторна робота 3 Постановка завдання Відповідно до заданого варіанта: 1. Отримати послідовність реалізацій випадкового вектора заданого обсягу (значень випадкової функції на заданому інтервалі часу). 2. Побудувати графік зміни реалізації випадкової функції та координатних функцій канонічного розкладу на заданому інтервалі часу. 3. Записати кількість реалізацій розподілів випадкового вектора. Індивідуальні завдання для моделювання Варіант 1 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 2 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 3 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 4 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки. Варіант 5 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с. Варіант 6 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Варіант 7 Змоделювати N = 10 реалізацій тривимірного випадкового вектора з математичним сподіванням
Варіант 8 Бортова система автоматичного управління ПС в режимі автоматичного заходу на посадку здійснює вихід літака на висоту прийняття рішення. Відхилення літака від рівносигнальних зон курсу і глісади в момент прольоту ВПР описується нормальним законом розподілу з параметрами: mx=0, тy= 0, σx = 3, σy = 2, kxy = 1.5. Змоделювати N = 20 реалізацій процесу заходу на посадку. Варіант 9 Проводиться стрільба по точковій цілі на площині. Розсіяння точки розриву снаряду проходить за нормальним законом, центр якого співпадає з ціллю (тх = ту = 0), а кореляційна матриця має вигляд:
Попадання в ціль відбувається, якщо відстань від неї до точки розриву снаряда не перевищує r0 = 10м. Змоделювати результати N = 10 пострілів і визначити кількість попадань. Варіант 10 Похибка автоматичної системи спостереження описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 0.01t і кореляційною функцією k(t, t+τ) = 1.2e-ατ cos βτ, де α = 0.05; β = 0.04. Отримати канонічний розклад випадкової функції і змоделювати реалізацію похибки на інтервалі [0, 100]с, з кроком дискретності τ = 10 с. Варіант 11 Частота обертання валу електродвигуна змінюється під впливом випадкових коливань напруги живлення і навантаження на валу і описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 3*103 sin0.2 t і кореляційною функцією k(t,t + τ) = Dt * е-ατ, де Dt = 20.5 t; α= 0.05. Отримати канонічний розклад випадкової функції і змоделювати реалізацію частоти обертання валу електродвигуна на інтервалі [0; 40] с, з кроком дискретності τ = 4 с. Варіант 12 Динамічна похибка систем автоматичної зміни частоти є нестаціонарний випадковий процес з нульовим математичним сподіванням і кореляційною функцією k(t,t + τ) = Dt * е-ατ cosβτ; Dt = 200 + 5 t; α =0.2; β =0.5. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію динамічної похибки системи на інтервалі [0; 20] с, з кроком дискретності τ = 2 с. Варіант 13 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 14 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 15 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 16 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки. Варіант 17 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с. Варіант 18 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Варіант 19 Змоделювати N = 10 реалізацій тривимірного випадкового вектора з математичним сподіванням
Варіант 20 Бортова система автоматичного управління ПС в режимі автоматичного заходу на посадку здійснює вихід літака на висоту прийняття рішення. Відхилення літака від рівносигнальних зон курсу і глісади в момент прольоту ВПР описується нормальним законом розподілу з параметрами: mx=0, тy= 0, σx = 3, σy = 2, kxy = 1.5. Змоделювати N = 20 реалізацій процесу заходу на посадку. Варіант 21 Проводиться стрільба по точковій цілі на площині. Розсіяння точки розриву снаряду проходить за нормальним законом, центр якого співпадає з ціллю (тх = ту = 0), а кореляційна матриця має вигляд:
Попадання в ціль відбувається, якщо відстань від неї до точки розриву снаряда не перевищує r0 = 10м. Змоделювати результати N = 10 пострілів і визначити кількість попадань. Варіант 22 Похибка автоматичної системи спостереження описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 0.01t і кореляційною функцією k(t, t+τ) = 1.2e-ατ cos βτ, де α = 0.05; β = 0.04. Отримати канонічний розклад випадкової функції і змоделювати реалізацію похибки на інтервалі [0, 100]с, з кроком дискретності τ = 10 с. Варіант 23 Частота обертання валу електродвигуна змінюється під впливом випадкових коливань напруги живлення і навантаження на валу і описується нестаціонарною випадковою функцією з математичним сподіванням m(t) = 3*103 sin0.2 t і кореляційною функцією k(t,t + τ) = Dt * е-ατ, де Dt = 20.5 t; α= 0.05. Отримати канонічний розклад випадкової функції і змоделювати реалізацію частоти обертання валу електродвигуна на інтервалі [0; 40] с, з кроком дискретності τ = 4 с. Варіант 24 Динамічна похибка систем автоматичної зміни частоти є нестаціонарний випадковий процес з нульовим математичним сподіванням і кореляційною функцією k(t,t + τ) = Dt * е-ατ cosβτ; Dt = 200 + 5 t; α =0.2; β =0.5. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію динамічної похибки системи на інтервалі [0; 20] с, з кроком дискретності τ = 2 с. Варіант 25 Стан блоку характеризується тривимірним вектором параметрів
Відхилення параметрів від номінальних значень описується сумісним нормальним розподілом з нульовим вектором середніх значень
Змоделювати стан вектора параметрів для N = 10 блоків. Варіант 26 Змоделювати N = 15 реалізацій нормального випадкового вектора
Варіант 27 Змоделювати N = 18 реалізацій систем двох випадкових величин (Х1,Х2), що підпорядковуються двомірному нормальному закону розподілу з параметрами: т1 = 3, т2 = 3.5, σ1 = 4, σ2 = 5, k12 = k21 = 7. Варіант 28 Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами: тх = 7, ту = 18, σ х = 2, σ y = 3, kху = 0. Змоделювати N = 25 реалізацій випадкової точки. Варіант 29 Процес зміни напруги на клемах генератора являє собою нестаціонарний випадковий процес, що задається математичним сподіванням m(t) = 20 – е–0.2t та кореляційною матрицею
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ =2с. Варіант 30 Відхилення параметра руху ПС від заданої траєкторії під час польоту в збудженій атмосфері є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією
де Dt = 5t + 350, α = 0.08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с. Лабораторна робота 4 Тоді
Розглянемо однорідні марківські процеси. Нехай процес починається зі стану Sі. Яка ймовірність того, що через m кроків процес перейде у стан Sj. Така ймовірність визначається рівнянням Кампорова-Чемпона
де 1 ≤ s ≤ m. Якщо відомо матрицю перехідних ймовірностей (або розміщений граф станів) і початковий розподіл (у момент часу t = 0) ймовірностей для усіх станів
де Постановка завдання Відповідно до заданого варіанта отримати послідовність вхідних сигналів, станів та вихідних сигналів на кожному з кроків. Індивідуальні завдання для моделювання Варіант 1 Спеціалізована операційна система приймає в обробку три класи завдань А, В і С з різним необхідним обсягом оперативної пам'яті. Імовірності появи завдань Р(А) = 0.5; Р(В) = 0.3; Р(С) = 0.2. В момент надходження завдання система може знаходитися в одному з двох станів: z1 – має вільні ресурси і може прийняти додаткові завдання; z2 – монополізована попередніми завданнями. Матриці перехідних імовірностей системи такі:
Вихідний сигнал – це стан системи в момент надходження чергового завдання. Змоделювати роботу ОС при надходженні k = 20 завдань, якщо функціонування системи починається за відсутності завдань. Варіант 2 Ремонтний цех АТБ, що включає в себе декілька ліній, здійснює обслуговування блоків АО з різним ступенем пошкодження. Можливі пошкодження трьох типів: А, В і С, імовірності появи яких Р(А) = 0,5; Р(В) = 0,15; Р(С) = 0,35. Блоки надходять у цех в дискретні моменти часу. Можливі стани цеху: z1 – є хоча б одна лінія, на яку надходить блок; z2 – всі лінії зайняті. Матриці перехідних імовірностей станів цеху:
Змоделювати роботу цеху з обслуговування к = 18 блоків, якщо в початковий момент всі лінії цеху вільні. Варіант 3 Система передачі даних має два незалежні канали. Через кожні 30 с надходять повідомлення для передачі. Кожний із каналів може знаходитися в одному з двох станів: z1 – вільний; z2 – зайнятий передачею повідомлення. Матриці перехідних імовірностей і початкових імовірностей першого і другого каналів відповідно мають вигляд:
Змоделювати стани системи передачі за 10 хв. Варіант 4 Процесор автоматизованої інформаційної системи може перебувати в одному зі станів: z1 - обробка інформації; z2 - простій через несправність процесора; z3 - простій через відсутність інформації. Контроль станів системи здійснюється через кожні 15 хв. Якщо виявлена несправність фахівці приступають до ремонту. Матриця початкових імовірностей станів системи має вигляд: Р(0) = (0,5 0,4 0,1), а матриця умовних перехідних імовірностей:
Змоделювати процес роботи системи за 5 год. Варіант 5 Електронний блок експлуатується в одному з таких режимів: Х1,Х2,Х3, імовірності виникнення яких відповідно Р(Х]) = 0.5; Р(Х2) = 0.3; Р(Х3) = 0.2. Інтенсивність відмов блоку залежить від режиму роботи. Стани блоку: z1 – справний; z2 – несправний. У випадку відмови блок відновлюється. Змоделювати стани блоку в дискретні моменти контролю tk, t= 1,2,...,20. Якщо в початковий момент роботи блок справний, а матриці перехідних імовірностей:
Варіант 6 Точка А „блукає” по осі абсцис відповідно до закону: на кожному кроці вона з імовірністю 0,5 залишається на місці, з імовірністю 0,3 зміщується на одиницю вправо і з імовірністю 0,2 – вліво. Промоделювати реалізацію переходів і визначити кінцевий стан точки А за k = 20 кроків, якщо її початковий стан – початок координат. Варіант 7 Тригер може знаходитися в одному з двох стійких станів: z1 = 0 і z2 = 1. Сукупність вхідних сигналів надходить у дискретні моменти часу t1, t2,... і приймає дві різні комбінації значень, які кодуються X1 і Х2, і переводять тригер з одного стану в інший. Тригер функціонує в стохастичних умовах під дією внутрішніх і зовнішніх випадкових збурень. Імовірності вхідних сигналів: Р(Х1) = 0.55; Р(Х2) = 0.45, матриці перехідних імовірностей:
Змоделювати переходи станів тригера за k = 20 тактів, якщо його початкові стани рівномірні. Варіант 8 ОС включає в себе два процесори. Завдання на обробку надходять кожні 30 хв. і залежно від складності займають один або два процесори. Система може знаходитись в станах: z1 – справні два процесори; z2 – справний перший процесор; z3 – справний другий процесор; z4 – обидва процесори несправні. Процесор, що вийшов з ладу, відновлюється. Змоделювати стан системи протягом 10 год, якщо в початковий момент два процесори справні, а матриці перехідних імовірностей кожного процесора мають вигляд:
Варіант 9 Двоканальна інформаційна система функціонує при різних рівнях сигналу, які змінюються стрибкоподібно і можуть бути віднесені до одного з двох класів А і В, що не перетинаються. В кожний момент контролю tk, k = 1,2,... система може знаходитися в одному зі станів: z1 – обидва канали в робочому стані; z2 – один канал несправний; z3 – система вийшла з ладу. Відомі імовірності появи сигналів: Р(А) = 0.7, Р(В) = 0.3, а також матриці перехідних ймовірностей системи: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , а якщо
, а якщо  , то відбудеться подія
, то відбудеться подія  .
. до
до 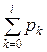 отриманих від генератора випадкових чисел ri означає, що відбулася подія Ai. Таку процедуру називають визначенням результату випробовування за жеребом.
отриманих від генератора випадкових чисел ri означає, що відбулася подія Ai. Таку процедуру називають визначенням результату випробовування за жеребом. Враховуючи, що ці події складають повну групу подій, тобто
Враховуючи, що ці події складають повну групу подій, тобто ,
,
 із заданим законом розподілу (табл. 1.1).
із заданим законом розподілу (табл. 1.1).






 з ймовірностями
з ймовірностями  , а функція розподілу дорівнює
, а функція розподілу дорівнює .
. , то моделювання випадкової дискретної величини виконується аналогічно моделюванню групи несумісних подій.
, то моделювання випадкової дискретної величини виконується аналогічно моделюванню групи несумісних подій.
 = (0,0,0) та кореляційною матрицею
= (0,0,0) та кореляційною матрицею
 з математичним сподіванням
з математичним сподіванням 




 .
.
 , можна знайти ймовірності станів
, можна знайти ймовірності станів  для будь-якого кроку за формулою:
для будь-якого кроку за формулою:
 - ймовірність переходу системи зі стану Sj → Si за k кроків.
- ймовірність переходу системи зі стану Sj → Si за k кроків.