
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сукупність усіх раціональних та ірраціональних чисел звуть дійсними числами.Содержание книги
Поиск на нашем сайте
Усі дійсні числа впорядковані за величиною, тобто для будь-яких двох чисел Абсолютна вартість числа. Абсолютною вартістю (або модулем) числа а зветься арифметична вартість цього числа
Властивості: За самим означенням 1. 2. Якщо 3. Доведення: Запишемо очевидні нерівності:
Метод математичної індукції поширює цю властивість на любу кількість доданків. 4. (Абсолютна вартість різниці не менша різниці абсолютних вартостей цих чисел). Доведення: Рівності Сталі і змінні величини. Величина зветься змінною, якщо вона може набирати різні числові вартості в умовах даної задачі. Сталою величиною звуть величину, яка має цілком певну вартість в умовах даної задачі або за будь-яких умов. Область змінювання змінної величини. Сукупність усіх числових вартостей, що їх може набувати змінна х, звуть областю чи обсягом змінювання цієї змінної. Приклад – радіус кола: Функціональна залежність. При дослідженні різноманітних явищ нас цікавлять не стільки змінні величини, взяті кожна окремо, скільки зв’язок між ними та залежність одних величин від інших. Абстрагуючись від конкретних залежностей між конкретними величинами, дамо означення функції. Нехай Х і У – деякі числові множини, а х і у – числа, які їм належать.
Змінна у зветься функцією змінної х, якщо будь-якій вартості х є Х за деяким правилом чи законом ставиться у відповідність одна певна вартість у є У. Це означення однозначної функції. Коли у відповідність х ставиться 2 чи більше вартостей у, то у звуть дво- або багатозначною функцією. Змінна х – аргумент, або незалежна змінна, у – функція, або залежна змінна. Символічний запис
Множина Х – область визначення функції, У – множина її значень. Функція, яка визначається з функціональної залежності Дану функцію Окремі вартості функції Приклад 1. Приклад 2. Відкритий проміжок, для якого дана точка, а є його серединою (центром) зветься околом цієї точки. Всі точки х, які справджують нерівність Класифікація функцій одного аргументу. 1. Ціла раціональна функція або многочлен.
2. Дробова-раціональна функція
(крім перелічених чотирьох дій при формуванні 1.+ 2. 3. Ірраціональна функція (при її формуванні до перелічених дій додається дія добування кореня). Наприклад, (1.+ 2.) + 3. 4. Трансцендентні функції – усякі неалгебраїчні функції. Найпростіші (елементарні) трансцендентні функції: а) показникова б) логарифмічна в) тригонометричні г) обернені тригонометричні функції Функції алгебраїчні, елементарні трансцендентні і їх комбінації називаються елементарні функції. Поняття зложеної (складеної) функції. Нехай
Приклади:
Границя функції Поняття границі функції – одне з найважливіших у вищій математиці. Нехай на деякій множині Χ визначена функція Означення. Число А називається границею функції 0 < виконується нерівність
Приклад 1. Покажемо, що функція Щоб це довести, ми повинні згідно з означенням для довільного ε > 0 вказати таке δ > 0, при якому із нерівності
Розглянемо Отже, оскільки Таким чином нерівність
виконується завжди для δ < ε. Тоді згідно з означенням Насправді визначення границі рідко використовується при обчисленні границь. Приклад 2. Знайти
Приклад 3. Знайти
Існують дві визначальні границі: 1. 2. Приклад 4. Знайти
Приклад 5. Знайти
Приклад 6. Знайти
Функція
Точка Якщо функція
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.008 с.) |

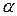 і
і  справедливе одне з трьох співвідношень
справедливе одне з трьох співвідношень  ;
;  ;
;  .
.
 .
. .
. .
.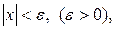 то
то  . Зокрема, коли
. Зокрема, коли  то
то  або
або  .
. .
. і
і 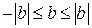 . Додамо їх почленно
. Додамо їх почленно (рівносильне)
(рівносильне)  .
. .
.
 і
і  майже очевидні і на них спинятися не будемо.
майже очевидні і на них спинятися не будемо.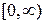 .
. .
. - характеристика функції, вона позначає те правило чи закон, який визначає у як функцію від х.
- характеристика функції, вона позначає те правило чи закон, який визначає у як функцію від х. зветься оберненою щодо даної функції
зветься оберненою щодо даної функції 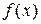 .
. часто звуть прямою. Очевидно, функції
часто звуть прямою. Очевидно, функції 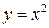 – пряма функція, а
– пряма функція, а  – їй обернена. Остання є двозначною.
– їй обернена. Остання є двозначною. і т.п. позначають символами
і т.п. позначають символами 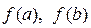 .
. ,
,  і
і 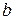 – дійсні,
– дійсні, 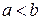 . Функція визначена для таких вартостей х, які справджують нерівності
. Функція визначена для таких вартостей х, які справджують нерівності 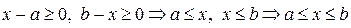 . Таким чином, для всіх вартостей х, між
. Таким чином, для всіх вартостей х, між  та
та  , функція у має дійсні вартості. Тут Х – це
, функція у має дійсні вартості. Тут Х – це  – замкнений проміжок.
– замкнений проміжок. . Функція визначена при
. Функція визначена при  , або
, або  . Тут Х – відкритий проміжок, або інтервал
. Тут Х – відкритий проміжок, або інтервал 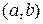 .
. , складають окіл точки
, складають окіл точки  .
.
 –ціле,
–ціле,  сталі (дії, за допомогою яких формується многочлен: додавання, віднімання, множення, піднесення до цілого додатнього степеня).
сталі (дії, за допомогою яких формується многочлен: додавання, віднімання, множення, піднесення до цілого додатнього степеня). .
. , використовується дія ділення)
, використовується дія ділення) раціональні функції.
раціональні функції. .
.


 .
. , а аргумент
, а аргумент  у свою чергу є деяка функція від
у свою чергу є деяка функція від 
 . Тоді, зрештою,
. Тоді, зрештою,  буде функцією від
буде функцією від  .
.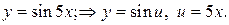


 ,
, – проміжні аргументи.
– проміжні аргументи.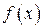 при
при  (або у точці
(або у точці 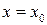 ), якщо для будь-якого ε > 0 можна знайти таке число
), якщо для будь-якого ε > 0 можна знайти таке число  > 0, що при всіх
> 0, що при всіх  , які задовольняють нерівність
, які задовольняють нерівність <
<  ,
, <
<  .
. має в точці
має в точці  0 границю, яка дорівнює 1.
0 границю, яка дорівнює 1. < δ випливала б нерівність
< δ випливала б нерівність < ε.
< ε.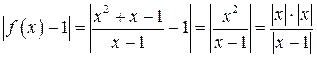 <
<  <1.
<1. .
.




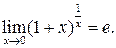
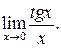







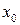 , якщо границя функції дорівнює її значенню в цій точці, тобто:
, якщо границя функції дорівнює її значенню в цій точці, тобто: (1)
(1) , що (за теоремою Вейєрштрасса)
, що (за теоремою Вейєрштрасса)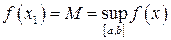 і
і 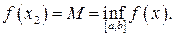 (2)
(2) 



