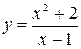Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило Лопіталя. Похідні вищих порядківСодержание книги Поиск на нашем сайте
Кажуть, що відношення двох функцій Розкрити ці невизначеності, тобто обчислити
Зауваження 1. Якщо похідні функцій Приклад 1. Обчислити
Приклад 2. Обчислити
Зауваження 2. Невизначеності виду Приклад 3. Знайти Маємо невизначеність
Приклад 4. Знайти Маємо невизначеність
Функція У механіці похідна другого порядку від функції Формула Тейлора. Нехай функція
Отже, формула Тейлора надає можливість розкласти функцію Зауваження. Формулою Маклорена називають формулу Тейлора (17) при Приклад 1. Знайти Маємо невизначеність
Тоді маємо:
Приклад 2. Знайти Маємо невизначеність
Дослідження функції на екстемум. Асимптоти графіка функцій Нехай функція Точка екстемуму Крім того, у точці локального мінімуму (максимуму) справедливе співвідношення
Точка Приклад 1. Дослідити функцію
Рис. 3.1. Дослідження функції
Рис. 3.2. Дослідження функції
Дослідимо, чи має дана функція точку перегину. Для цього знайдемо другу похідну і прирівняємо її до нуля: Рис. 3.2 видно, що
2
-4 -2 -1 0 1 2 Рис. 3.3. Графік функції
При дослідженні поведінки функції на нескінченності та поблизу точок розриву (невизначеності) часто виявляється, що графік функції як завгодно близько наближається до тієї чи іншої прямої. Такі прямі називаються асимптотами. Існують три види асимптот: вертикальні, горизонтальні і нахилені. Пряма
Якщо коефіцієнт Пряма Приклад 2. Знайти асимптоти графіка функції За формулою (18) знаходимо коефіцієнти
Отже, пряма Нарешті, точка
-10
-2 -1 0 1 2
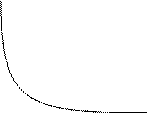
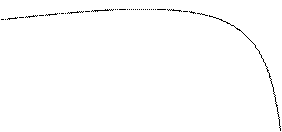
Рис. 3.4. Графік функції Наведемо загальну схему для побудови графіка функції 1. Знайти область визначення функції. 2. Знайти точки перетину графіка функції з віссю ординат (покласти у формулі, яка задає функцію, х = 0) і віссю абсцис (розв’язати рівняння 3. Знайти асимптоти функції. 4. Дослідити функцію на екстремум: знайти точки мінімуму, максимуму, а також точки перегину. Обчислити значення функції у цих точках. Встановити ділянки монотонності функції. 5. Побудувати схематичний графік функції При побудові графіка важливо врахувати його симетрію. Для цього корисно перевірити функцію на парність (непарність). Зауваження. Функція Також важливо перевірити функцію на періодичність: Приклад 3. Побудувати графік функції Згідно з наведеною вище схемою: 1. Область визначення функції 2. Графік даної функції перетинає вісь ординат у точці 3. Дослідимо поведінку функції поблизу точки розриву х = 1. Маємо:
Рис. 3.5. Дослідження функції Отже, пряма 4. Знайдемо першу похідну функції і прирівняємо її до нуля:
Відмітивши ці точки на осі х (Рис. 3.5), дослідимо їх на екстремум. Отже,
5. Дана функція не є парною і не є непарною. Її графік наведено на Рис. 3.6.
-2 -1 0 1 2 3
Рис. 3.6. Графік функції
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.243.161 (0.01 с.) |

 при
при  є невизначеністю виду
є невизначеністю виду 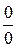 або
або  , якщо
, якщо  або
або 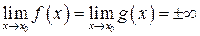 відповідно.
відповідно.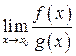 , надає можливість правило Лопіталя: якщо існує границя відношення похідних
, надає можливість правило Лопіталя: якщо існує границя відношення похідних  (скінченна або нескінченна), тоді існує і границя
(скінченна або нескінченна), тоді існує і границя 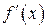 і
і 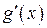 задовольняють тим самим вимогам, що і самі функції
задовольняють тим самим вимогам, що і самі функції 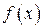 і
і 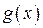 при
при  .
.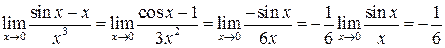 .
. .
. .
. для функції
для функції 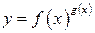 за допомогою тотожного перетворення
за допомогою тотожного перетворення 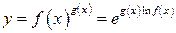 можна привести до невизначеності
можна привести до невизначеності  . Остання невизначеність легко зводиться до невизначеності
. Остання невизначеність легко зводиться до невизначеності 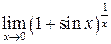 .
. .
.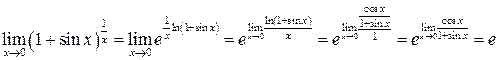 .
.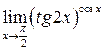 .
.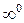 .
.
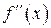 . Похідні, починаючи з другої, називаються похідними вищих порядків:
. Похідні, починаючи з другої, називаються похідними вищих порядків: 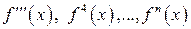 . Отже, похідна п -го порядку
. Отже, похідна п -го порядку 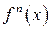 є похідна від похідної (п - 1)-го порядку.
є похідна від похідної (п - 1)-го порядку. , яка описує траєкторію руху матеріальної точки, має фізичний зміст, а саме визначає прискорення точки в момент часу
, яка описує траєкторію руху матеріальної точки, має фізичний зміст, а саме визначає прискорення точки в момент часу 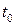 :
: 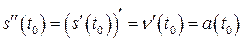 .
. має в точці
має в точці 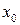 і деякому її околі похідні порядку п +1. Це означає, що функція
і деякому її околі похідні порядку п +1. Це означає, що функція 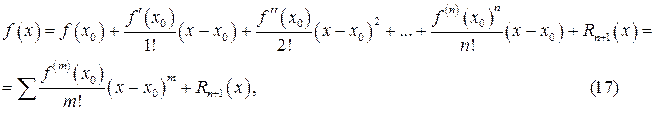 де
де 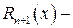 деякий залишковий член, причому
деякий залишковий член, причому 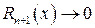 при
при  (0!=1 у формулі (17)).
(0!=1 у формулі (17)). .
. .
.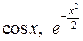 і
і 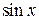 у ряд Маклорена з необхідною точністю:
у ряд Маклорена з необхідною точністю:


 .
.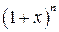 в ряд Маклорена:
в ряд Маклорена: 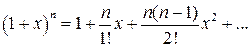 У результаті отримуємо:
У результаті отримуємо: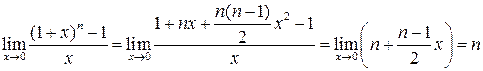 .
. диференційована на інтервалі
диференційована на інтервалі  . Точка
. Точка  називається точкою екстремуму, якщо
називається точкою екстремуму, якщо  .
.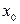 називається локальним мінімумом (максимумом), якщо
називається локальним мінімумом (максимумом), якщо 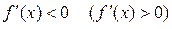 ліворуч від цієї точки і
ліворуч від цієї точки і 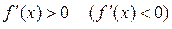 праворуч від цієї точки.
праворуч від цієї точки.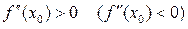 .
. і 2)
і 2) 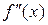 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 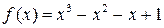 на екстремум.
на екстремум. Знаходимо похідну і прирівнюємо її нулю:
Знаходимо похідну і прирівнюємо її нулю:  . Отже, точками екстремуму є
. Отже, точками екстремуму є  і
і 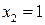 . Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції
. Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції 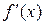 в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі (
в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі ( )
) 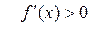 (функція
(функція 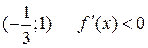 (функція
(функція 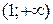
 (функція
(функція 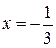 має локальний максимум
має локальний максимум 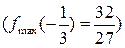 , а у точці х= 1 – локальний мінімум
, а у точці х= 1 – локальний мінімум  . Дійсно,
. Дійсно,  і
і  .
.




 x
x 1
1
 х
х . З
. З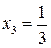 і, отже, дана точка є точкою перегину функції
і, отже, дана точка є точкою перегину функції 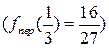 . Її графік наведено на Рис. 3.3.
. Її графік наведено на Рис. 3.3.




 4 у
4 у


 0
0 
 -2
-2

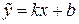 називається нахиленою асимптотою графіка функції
називається нахиленою асимптотою графіка функції 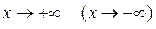 , де
, де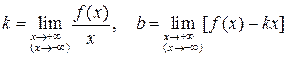 . (18)
. (18)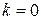 , тоді така асимптота називається горизонтальною
, тоді така асимптота називається горизонтальною  .
.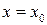 називається вертикальною асимптотою графіка функції
називається вертикальною асимптотою графіка функції  (або
(або  ).
). .
. і
і 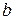 нахиленої асимптоти:
нахиленої асимптоти:
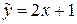 є нахиленою асимптотою графіка даної функції
є нахиленою асимптотою графіка даної функції  , так і при
, так і при  . Оскільки
. Оскільки 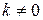 , то горизонтальних асимптот немає.
, то горизонтальних асимптот немає.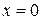 є точкою розриву даної функції
є точкою розриву даної функції  . Отже, пряма
. Отже, пряма 

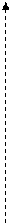


 20
20
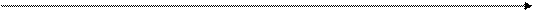
 у
у
 10
10


 0
0







 0 х
0 х

 :
: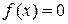 )
)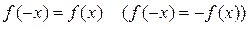 .
.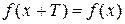 , де
, де 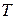 – період функції
– період функції 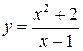 .
. (точка х = 1 є точкою розриву).
(точка х = 1 є точкою розриву).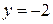 (при
(при 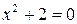 не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис.
не має дійсних коренів, то графік даної функції взагалі не перетинає вісь абсцис. . Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо:
. Отже, пряма х = 1 є вертикальною асимптотою. За формулами (18) знаходимо: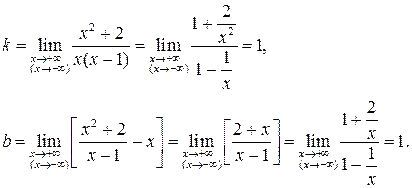
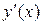 + max – – min +
+ max – – min +




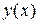
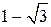 1
1  x
x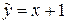 є нахилена асимптота даної функції. Горизонтальних асимптот немає.
є нахилена асимптота даної функції. Горизонтальних асимптот немає.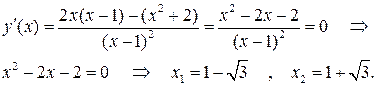
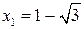 є точкою максимуму,
є точкою максимуму, 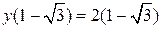 , а
, а 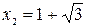 є точкою мінімуму,
є точкою мінімуму, 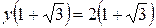 . Функція зростає на інтервалах
. Функція зростає на інтервалах 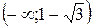 і
і  . Функція спадає на інтервалі
. Функція спадає на інтервалі  . З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну:
. З’ясуємо, чи має дана функція точку перегину. Знайдемо її другу похідну: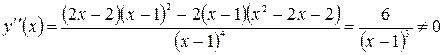 . Отже, точок перегину функція немає.
. Отже, точок перегину функція немає.



 40 y
40 y 30
30 20
20

 10
10  0
0


 0
0  1 x
1 x -20
-20




 -40
-40