
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над комплексными числами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Треугольник Паскаля Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
6. Числовые множества. Ограниченность множества. Граничная точка. Граница множества. Числовые множества В математике чаще всего мы имеем дело с множествами элементов которыми являются числа. Такие множества называются числовыми. Для некоторых часто встречающихся числовых множеств в школьном курсе математики приняты стандартные обозначение: N - множество натуральных чисел, Z - множество целых чисел, Q - множество рациональных чисел, R - множество действительных чисел. Ограниченность Множества Говорят, что множество X ⊂ R ограничено сверху, если существует число c ∈ R такое, что x 6 c для любого x ∈ X.Число c при этом называется верхней границей множества X. Аналогично определяются ограниченность множества снизу и нижняя граница множества X. Множество, ограниченное и сверху, и снизу, называется Ограниченным. Элемент a ∈ X называется наибольшим (или максимальным) элементом множества X ⊂ R, если x 6 a для любого элемента x ∈ X (аналогично определяется наименьший (минимальный) элемент множества X). В этом случае пишут a = max X (a = min X).
Пример 1.4.1. 1) X = {3, 8, 9}, 3 = min X; 9 = max X; 2) X = [1, 3], 1 = min X; 3 = max X; 3) X = [1, 3), 1 = min X; максимального элемента в этом множестве не существует. Лемма 1.4.1. Если максимальный (минимальный) элемент существует, то он единственный. Число c ∈ R называется точной верхней границей множества X ⊂ R, если выполнены следующие два условия: 1) любой элемент x ∈ X удовлетворяет неравенству x 6 c; 2) для любого ε > 0 существует элемент x0 ∈ X такой, что c − ε < x0. В этом случае пишут S = sup X ("супремум" X). Это определение говорит о том, что c наименьшая из верхних границ. Аналогично определяется точная нижняя граница s множества X, которая обозначается s = inf X ("инфимум" X). Пример 1.4.2. 1) X = [1, 3) 1 = inf X, 3 = sup X; 2) X = (1, 3] 1 = inf X, 3 = sup X. Для неограниченных сверху множеств X пишут sup X = +∞, а для
неограниченных снизу множеств X пишут inf X = −∞.
7. Комплексные числа. Операции над комплексными числами. Формула Муавра. Комплексные числа - это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или мнимая единица. i 2= - 1 Любое комплексное число состоит из двух частей: вещественной и мнимой:
Операции над комплексными числами. На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами. Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор. Сложение.
1.2 Вычитание, аналогично, производится по следующему правилу:
Умножение.
Деление. Определяется просто как обратная операция к умножению.
Формула Муавра zn = rn (cos n φ + i sin n φ ). С помощью формулы Муавра можно получить формулы, выражающие cos nφ и sin n φ через синус и косинус числа φ:
8. Многочлены. Теорема о делении с остатком. Наибольший общий делитель многочленов. Алгоритм Евклида. Многочлены Многочленом (полиномом) n -й степени относительно переменной величины x называется выражение вида P (x)= a 0 xn + a 1 xn −1+...+ an −1 x + an,
Многочлен первой степени также называют линейным многочленом, многочлен второй степени - квадратным, а многочлен третьей степени -- кубичным многочленом. Два многочлена P (x) и Q (x) считаются равными (или тождественно равными), если равны их коэффициенты при одинаковых степенях переменной x, и пишут P (x)= Q (x). Деление с остатком Определение. Пусть Полином Пример.
Теорема. (о делении с остатком). Пусть
Доказательство. Существование. Пусть
Предположим, что теорема верна не для любого полинома
Пусть
Коэффициент при
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна. Единственность. Предположим, что 1) 2)
Алгоритм Евклида Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел. Корни Многочлена Как мы видели выше, методом выделения полного квадрата можно найти корни квадратного трехчлена. В случае многочленов высших степеней найти корни становится гораздо труднее, а иногда и просто невозможно. Попробуем это сделать там, где это достаточно просто. Рассмотрим многочлен
где a 1, a 2,..., an − целые числа, an ≠ 0.
Теорема Безу Теорема Безу. Если многочлен Схема Горнера Схема сокращенного деления многочлена на двучлен. При делении многочлена Теорема виета Для приведенного квадратного уравнения (т.е. такого, коэффициент при x2 в котором равен единице) x2 + px + q = 0 сумма корней равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q: В случае неприведенного квадратного уравнения ax2 +bx+c =0: 10. Рациональные функции. Представление рациональной функции в виде суммы простейших дробей. Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где Частным случаем являются рациональные функции одного переменного:
Другим частным случаем является отношение двух линейных функций — дробно-линейная функция. Матрица Матрицей размера m на n (записывается так Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами:
Операции над матрицами 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B, т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц 6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Свойства сложения матриц
A + (– A) = A – A = 0, где 0 – матрица, составленная из нулевых элементов.
Свойства, связанные с умножением матриц.
12. Обратная матрица. Алгоритм нахождения обратной матрицы. Свойства обратных матриц.
Обратная Матрица Рассмотрим квадратную матрицу Обозначим Δ =det A. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0. Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица матрице А, обозначается через А-1, так что В = А-1 и вычисляется по формуле где А i j - алгебраические дополнения элементов a i j матрицы A.. Вычисление A-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицы можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Свойства Обратной матрицы Понятие обратной матрицы, равенство
13. Ранг матрицы. Свойства ранга матрицы. Элементарные преобразования матрицы. Ранг матрицы Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля. Свойства ранга матрицы 1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы. 2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец. Элементарные преобразования матрицы 1) умножение какой-нибудь строки (столбца) на отличное от нуля число; 2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число; 3) перестановку местами любых двух строк (столбцов).
14. Системы линейных уравнений. Однородные и неоднородные системы. Совместность системы. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно. Однородные системы
всегда является совместной. Доказательство. Для этой системы набор чисе
В этом разделе мы будем использовать матричную запись системы: Предложение 15.3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением. Доказательство. Пусть
Так как Пусть
Так как
Следствие 15.1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений.
Действительно, умножая ненулевое решение на различные числа, будем получать различные решения. Определение 15.5 Будем говорить, что решения Определение 15.6 Пусть
где Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях Как находить фундаментальную систему решений мы увидим позже, в разделе "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)". Теорема 15.3 Пусть Неоднородные системы Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно n неизвестных
В отличие от однородной системы, эта система совместна не всегда. Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
15. Метод Крамера для нахождения решения системы линейных уравнений. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод. Для системы
с определителем матрицы системы
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В этой форме формула Крамера справедлива без предположения, что
16. Матричный метод решения систем линейных уравнений. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с
Тогда её можно переписать в матричной форме:
Умножим это матричное уравнение слева на Так как
Для однородной системы линейных уравнений, то есть когда вектор
17. Метод Гаусса для нахождения решения системы линейных уравнений. Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Решение. Выпишем расширенную матрицу данной системы и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: б) третью строку умножим на (-5) и прибавим к ней вторую: В результате всех этих преобразований данная система приводится к треугольному виду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
18. Понятие вектора. Линейные операции над векторами. Вектором (в реальном пространстве) называется направленный отрезок Проекция вектора на ОСЬ Проекция вектора на ось это отрезок заключенный между перпендикулярами проведёнными от концов вектора к оси....
Длина Вектора Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль. Длина вектора на плоскости вычисляется по следующей формуле:
Длина вектора в трехмерном пространстве вычисляется по следующей формуле:
Формула длины вектора в n -мерном пространстве:
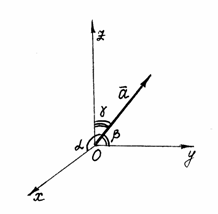
Направление вектора в пространстве определяется углами
Рис. 12 Из свойств проекций: Легко показать, что 1) 2) координаты любого единичного вектора совпадают с его направляющими косинусами:
20. Скалярное, векторное, смешанное произведения векторов. Скалярным произведением в векторном пространстве 1. для любых трех элементов 2. для любых 3. для любого Векторным произведением вектора · длина вектора · вектор · вектор · в случае пространства Обозначение:
Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным. Заметим, что из п.2 определения следует, что Прямая на плоскости В декартовой системе координат на плоскости каждая прямая определяется уравнением 1–й степени и, обратно, каждое уравнение 1–й степени определяет прямую. Уравнение вида Ax + By + Cz = 0 (A2 + B2 ≠ 0) называется общим уравнением прямой. Любой вектор, перпендикулярный прямой, называется нормальным вектором и обозначается
. Например,
= {A, B}. Угловым коэффициентом k прямой называется число k = tgα, где α — угол наклона прямой к оси OX (0 ≤ α < π). Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом (b — ордината точки пересечения прямой с осью OY). Уравнение прямой
+
= 1 называется уравнением прям |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.246.21 (0.017 с.) |

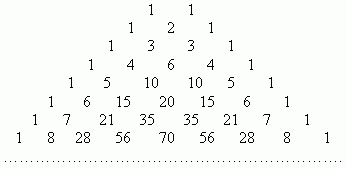


 .
.



 и
и  — многочлены,
— многочлены,  . Будем говорить, что
. Будем говорить, что  , где
, где  и
и  — многочлены, причем
— многочлены, причем  .
. .
.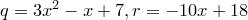 .
. ,
,  и
и  . Положим
. Положим  .
. .
. :
:
 . Положим
. Положим
 в многочлене
в многочлене  равен
равен  . Следовательно,
. Следовательно,  . Значит, для многочлена
. Значит, для многочлена  и
и  . Тогда
. Тогда

 . Значит,
. Значит,  ,
, .
.


 то число p является делителем числа
то число p является делителем числа  (свободного члена), а число q является делителем числа
(свободного члена), а число q является делителем числа 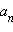 (старшего коэффициента).
(старшего коэффициента).
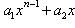
 разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn (a).
разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn (a).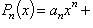

 , расположенного по убывающим степеням x, на двучлен x - a применяется метод сокращенного деления, называемый схемой Горнера.
, расположенного по убывающим степеням x, на двучлен x - a применяется метод сокращенного деления, называемый схемой Горнера.
 ,
,  — многочлены от любого числа переменных.
— многочлены от любого числа переменных.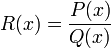 , где P(x) и Q(x) — многочлены.
, где P(x) и Q(x) — многочлены. )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
)называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца. - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом
- элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом






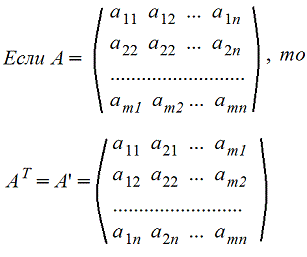
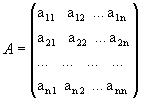 .
. , (1)
, (1) , свойства операций над матрицами и свойства определителя матрицы позволяют обосновать следующие свойства обратной матрицы:
, свойства операций над матрицами и свойства определителя матрицы позволяют обосновать следующие свойства обратной матрицы: .
. .
. .
. .
.

 ,
,  ,
,  ,
, 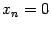 является решением.
является решением. .
. и
и  служат решениями системы
служат решениями системы 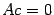 и
и  . Пусть
. Пусть  . Тогда
. Тогда
 , то
, то  -- решение.
-- решение.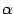 -- произвольное число,
-- произвольное число, 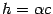 . Тогда
. Тогда
 , то
, то  -- решение.
-- решение. системы
системы 
 -- произвольные числа, будем называть общим решением системы
-- произвольные числа, будем называть общим решением системы  , где
, где  -- число неизвестных в системе.
-- число неизвестных в системе.
 линейных уравнений с
линейных уравнений с 
 , отличным от нуля, решение записывается в виде
, отличным от нуля, решение записывается в виде

 и
и  , либо набор
, либо набор 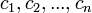 состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама иЛеммы Накаямы.
состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама иЛеммы Накаямы.
 , где
, где  — основная матрица системы,
— основная матрица системы,  и
и  — столбцы свободных членов и решений системы соответственно:
— столбцы свободных членов и решений системы соответственно: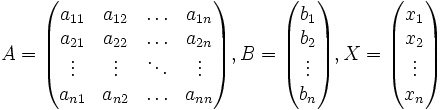
 — матрицу, обратную к матрице
— матрицу, обратную к матрице 
 , получаем
, получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: .
.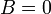 , действительно обратное правило: система
, действительно обратное правило: система 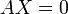 имеет нетривиальное (то есть ненулевое) решение только если
имеет нетривиальное (то есть ненулевое) решение только если 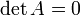 . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
 ;
;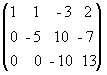 .
. с начальной точкой
с начальной точкой 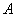 и конечной точкой
и конечной точкой  , который можно передвигать параллельно самому себе. Таким образом, считается, что два направленных отрезка
, который можно передвигать параллельно самому себе. Таким образом, считается, что два направленных отрезка  , имеющие равные длины (
, имеющие равные длины ( ) и одно и то же направление, определяют один и тот же вектор
) и одно и то же направление, определяют один и тот же вектор  , и в этом смысле пишут
, и в этом смысле пишут 




 , которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:
, которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:  ,
,  ,
,  .
.
 ,
,  ,
,  . Следовательно,
. Следовательно, ,
, 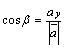 ,
,  . (2.5)
. (2.5) ;
; .
. над полем
над полем  комплексных (или
комплексных (или  вещественных) чисел называется функция
вещественных) чисел называется функция  для элементов
для элементов  , принимающая значения в
, принимающая значения в  и
и  пространства
пространства  из
из  (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу);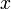 и
и  , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность); , причем
, причем  только при
только при  (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения).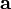 на вектор
на вектор  в пространстве
в пространстве  называется вектор
называется вектор 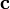 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям: между ними:
между ними:  ;
; является правой;
является правой; требуется ассоциативность тройки векторов
требуется ассоциативность тройки векторов  .
.
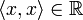 . Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.
. Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.


