
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономический смысл производнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Экономический смысл производной: производительность труда есть производная объема произведенной продукции по времени. Производная логарифмической функции Пример 7. Объем продукции Производительность труда выражается производной
а скорость и темп изменения производительности – соответственно производной
Итак, к концу работы производительность труда существенно снижается; при этом изменение знака Рассмотрим еще одно понятие, иллюстрирующее экономический смысл производной. Обозначим через
Если объем производства увеличится на Среднее приращение издержек выражается отношением Под предельными издержками производства понимают предел среднего приращения издержек при безграничном уменьшении
Предел (1) выражает дополнительные затраты на производство продукции при увеличении объема производства на малую единицу, если исходный объем производства составляет ^ Экономический смысл производной в данной точке: производная выражает предельные издержки производства при данном объеме и характеризует приблизительно дополнительные затраты на производство единицы дополнительной продукции.
41. Производные основных элементарных функций. Основные правила дифференцирования. ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Правила дифференцирования Основные правила дифференцирования Правило 1. Если функции
дифференцируемы в некоторой точке
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций. Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
Правило 2. Если функции
и
дифференцируемы в некоторой точке
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой. Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные. Например, для трёх множителей имеем:
и
дифференцируемы в некоторой точке
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. 42. Производные высших порядков. Механический смысл второй производной. Производные высших порядков Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
Если функция
Пусть теперь производная
Если функция
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1070; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.68.177 (0.01 с.) |

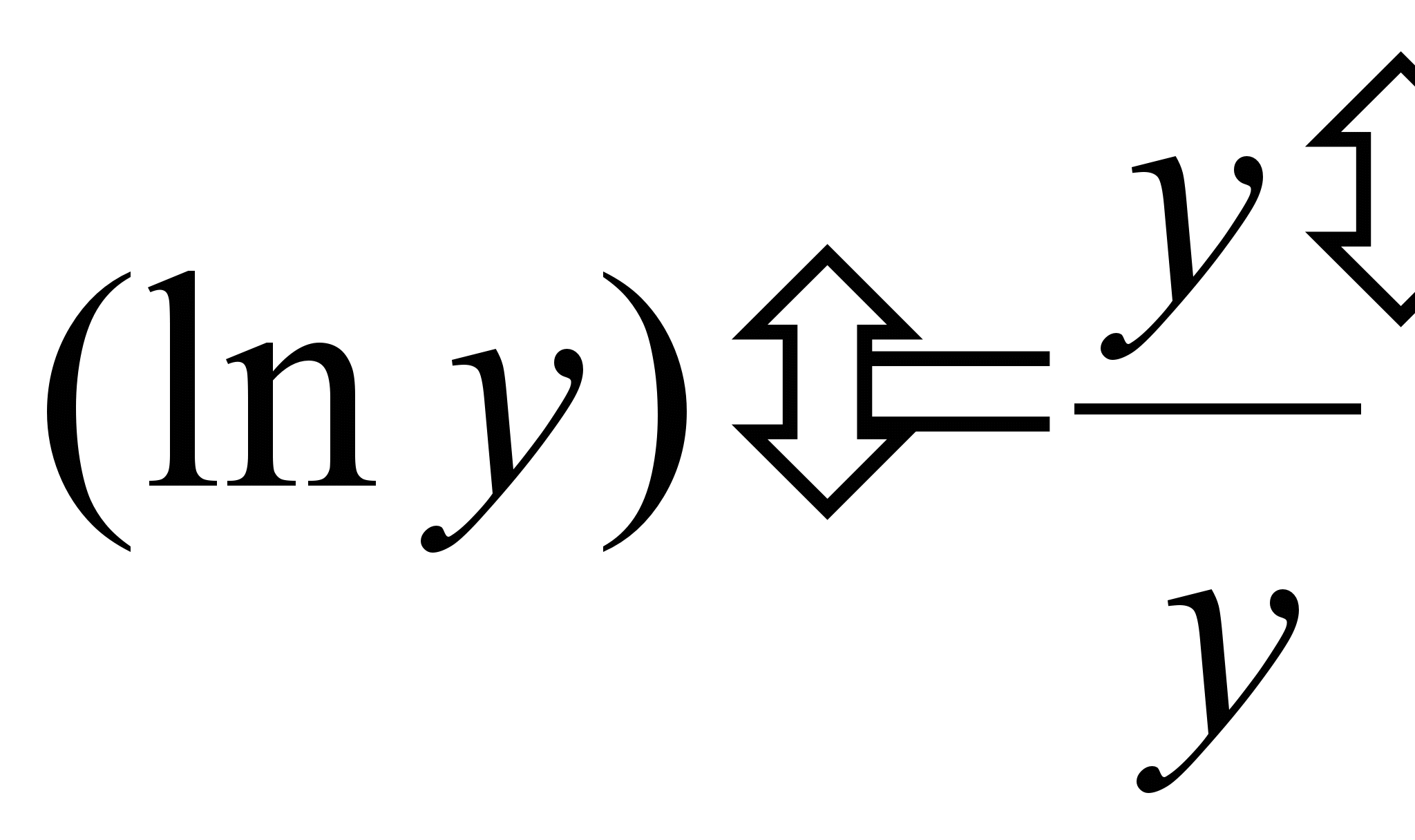 называется логарифмической производной, а так же относительной скоростью изменения функции или темпом изменения функции.
называется логарифмической производной, а так же относительной скоростью изменения функции или темпом изменения функции. , произведенной бригадой рабочих, может быть описан уравнением
, произведенной бригадой рабочих, может быть описан уравнением 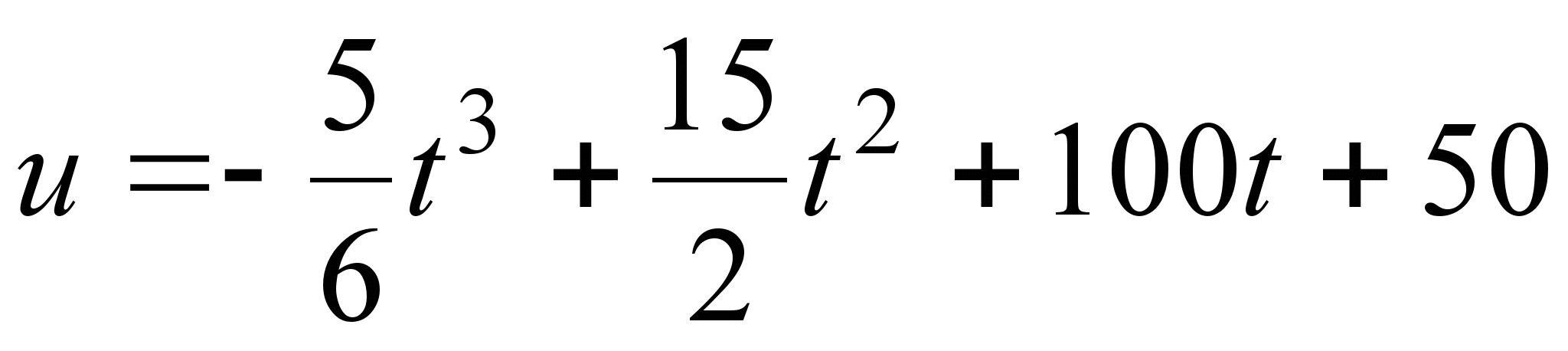 ,
,  , где
, где  - рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
- рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.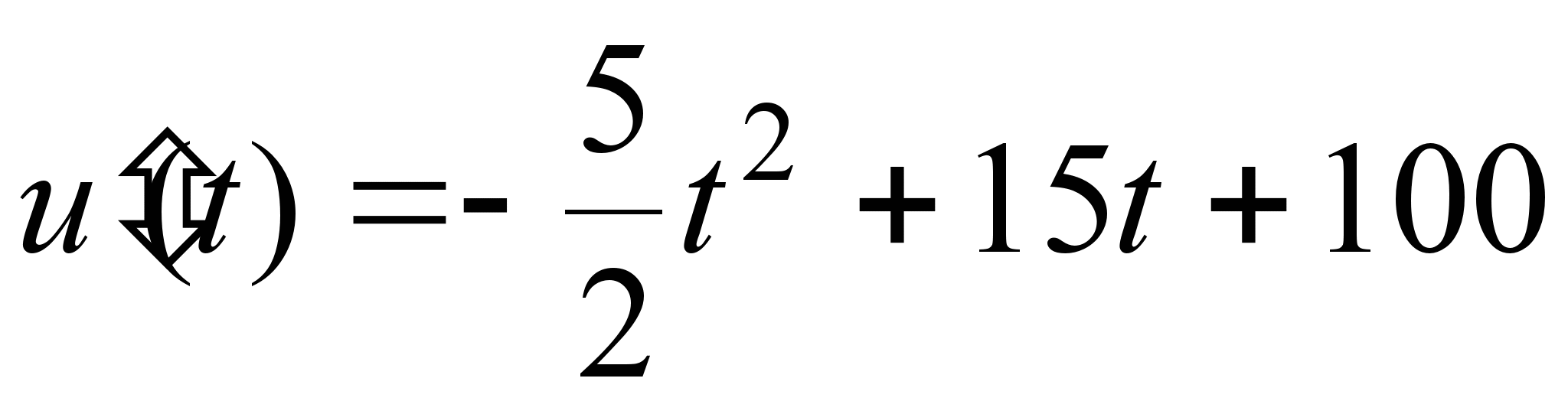 ,
, и логарифмической производной
и логарифмической производной 

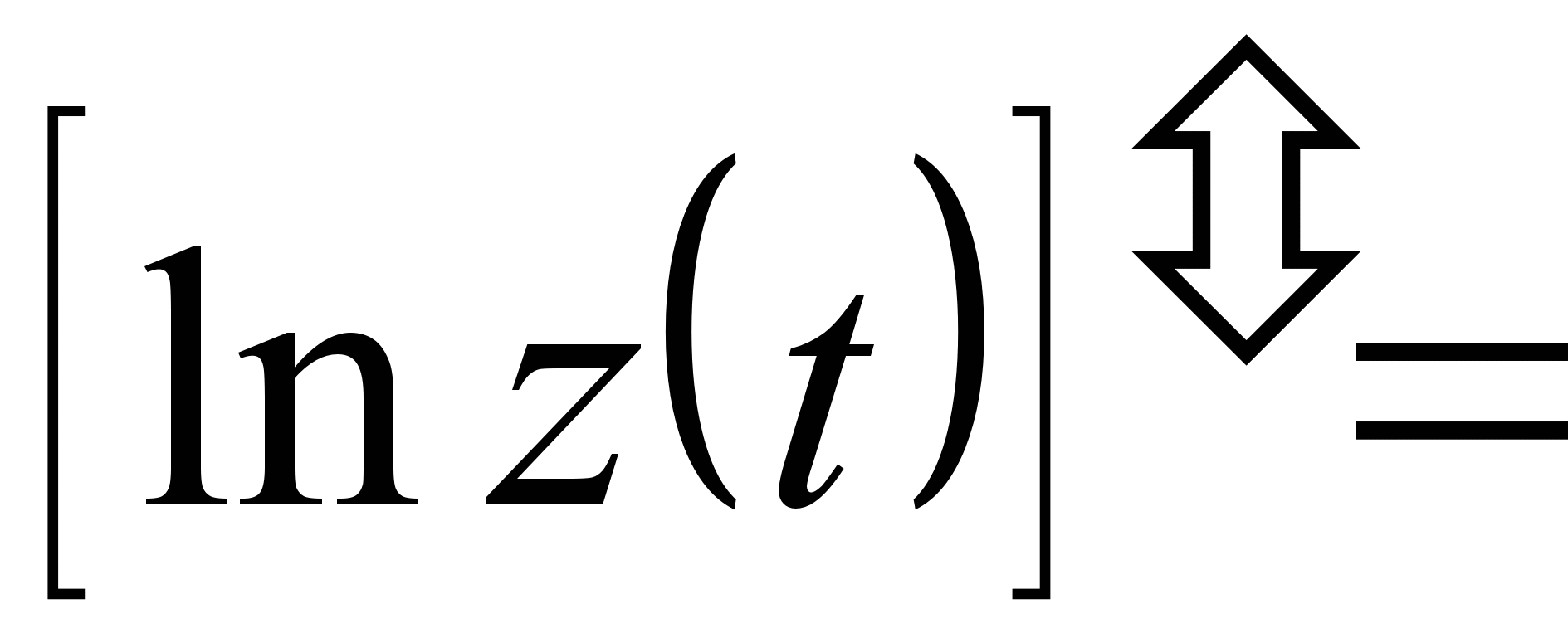

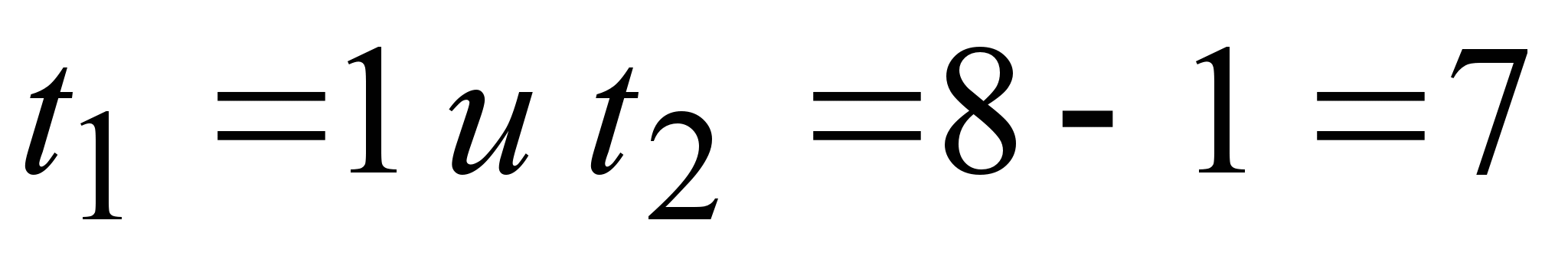 соответственно имеем:
соответственно имеем: 

 объем производства некоторой продукции, через
объем производства некоторой продукции, через 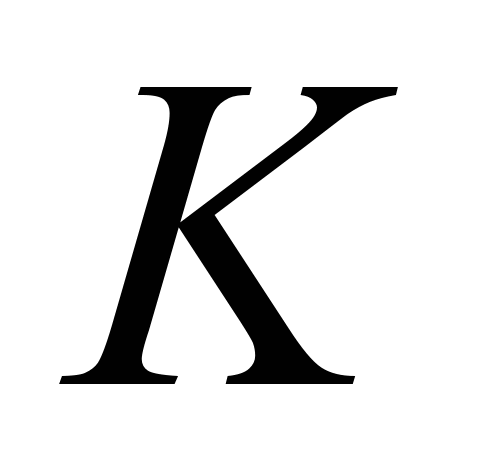 - суммарные затраты или издержки производства. Производственная функция (функция затрат) описывает зависимость издержек производства
- суммарные затраты или издержки производства. Производственная функция (функция затрат) описывает зависимость издержек производства  .
.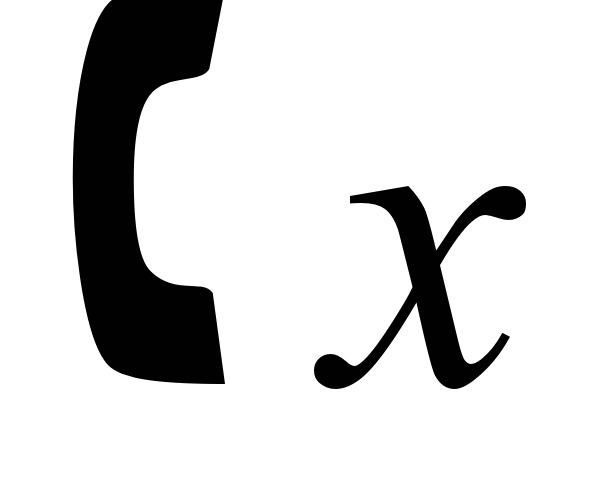 единиц, то затраты возрастут на
единиц, то затраты возрастут на  единиц.
единиц. .
. . (1)
. (1)




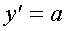



























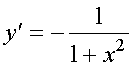
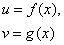
 , то в той же точке дифференцируемы и функции
, то в той же точке дифференцируемы и функции
 (5)
(5) (6)
(6)


 (7)
(7) (8)
(8) (9)
(9) , то в этой точке дифференцируемо и их частноеu/v, причём
, то в этой точке дифференцируемо и их частноеu/v, причём (10)
(10)
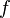 дифференцируема в
дифференцируема в  , то производная первого порядка определяется соотношением
, то производная первого порядка определяется соотношением
 -го порядка
-го порядка  определена в некоторой окрестности точки
определена в некоторой окрестности точки 
 имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от
имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от  может иметь в некоторой точке
может иметь в некоторой точке  частные производные по той же или по любой другой переменной. Для исходной функции
частные производные по той же или по любой другой переменной. Для исходной функции  или
или 
 или
или 



