
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные функции двух переменныхСодержание книги
Поиск на нашем сайте
Переменная z называется функцией двух независимых переменных х и у на некотором множестве точек Пишут:
С геометрической точки зрения функция Если при Таким образом, по определению
Аналогично,
Так как
Пример 1 Найти частные производные функции Решение
Пример 2 Показать, что функция Решение Найдем частные производные
Подставим найденные выражения в левую часть уравнения:
Дифференциал функции двух переменных
Частным дифференциалом функции выражение выражение
Пример 1 Найти частные дифференциалы функции
Решение
Полный дифференциал функции
Пример 2 Найти дифференциал Решение Найдем частные производные
Подставим частные производные в формулу полного дифференциала, получим
Касательная плоскость и нормаль к поверхности
Прямая линия называется касательной к поверхности в некоторой точке Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
Если уравнение поверхности задано неявно, т.е.
Если уравнение поверхности задано в явном виде, т.е.
Нормалью к поверхности называют прямую, перпендикулярную к касательной плоскости в точке касания. Если уравнение поверхности задано неявно, т.е.
Если уравнение поверхности задано в явном виде, т.е.
Пример Составить уравнения касательной плоскости и нормали к поверхности Решение Найдем частные производные
Уравнение касательной плоскости:
Уравнение нормали:
Производная по направлению и градиент
Пусть функция Производная функции
где
Производная по направлению является скоростью изменения функции Абсолютная величина производной по направлению
Градиентом функции
т.е. вектор, проекции которого на координатные оси Ох, Оу, Oz равны соответственно частным производным по х, у, z в точке Градиент U в данной точке по численному значению и по направлению характеризует наибольшую скорость возрастания величины U.
Пример Для функции Решение Градиент находим по формуле
Производная по направлению: где
Краткое содержание (программа) курса
Элементы линейной алгебры Матрицы, операции над ними. Определители и их свойства и вычисление. Ранг матрицы, обратная матрица. Теорема Кронекера-Капелли. Решение систем линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса. Система m линейных уравнений с n неизвестными.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.190.43 (0.009 с.) |

 , если каждой паре значений
, если каждой паре значений  из множества
из множества 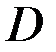 соответствует определенное значение величины z.
соответствует определенное значение величины z. .
. представляет собой поверхность.
представляет собой поверхность. отношение частного приращения функции к вызвавшему его приращению аргумента
отношение частного приращения функции к вызвавшему его приращению аргумента  имеет конечный предел, то этот предел называется частной производной функции
имеет конечный предел, то этот предел называется частной производной функции  по независимой переменной х в точке
по независимой переменной х в точке  и обозначается
и обозначается 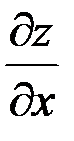 , или
, или  , или
, или  .
. .
. .
. вычисляется при неизменном значении переменной у, а
вычисляется при неизменном значении переменной у, а 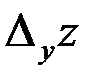 – при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции
– при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции  называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции
называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции  называется ее производная по у, вычисленная в предположении, что х – постоянная.
называется ее производная по у, вычисленная в предположении, что х – постоянная. .
.
 удовлетворяет уравнению
удовлетворяет уравнению  .
. ,
, .
.
 что и требовалось доказать.
что и требовалось доказать. называется произведение частной производной на соответствующее произвольное приращение независимой переменной:
называется произведение частной производной на соответствующее произвольное приращение независимой переменной: называется частным дифференциалом функции
называется частным дифференциалом функции  по переменной х;
по переменной х; называется частным дифференциалом функции
называется частным дифференциалом функции  по переменной у.
по переменной у.
 ,
,  .
. равен сумме ее частных дифференциалов:
равен сумме ее частных дифференциалов: .
. функции
функции  .
. ,
, .
. .
. , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку
, если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку  .
. , называется касательной плоскостью к поверхности в точке
, называется касательной плоскостью к поверхности в точке  .
.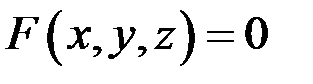 , то уравнение касательной плоскости к поверхности в точке
, то уравнение касательной плоскости к поверхности в точке 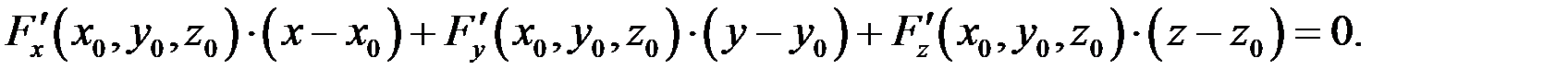
 , то уравнение касательной плоскости к поверхности имеет вид
, то уравнение касательной плоскости к поверхности имеет вид .
. .
. .
. в точке
в точке  .
. и вычислим их значения в точке
и вычислим их значения в точке  .
. или
или  .
. .
.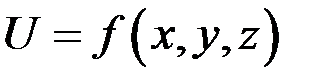 дифференцируема в точке
дифференцируема в точке  .
. по направлению вектора
по направлению вектора  находится по формуле
находится по формуле ,
,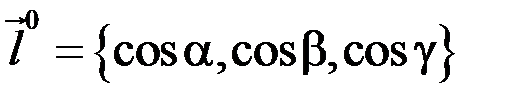 – единичный вектор заданного направления
– единичный вектор заданного направления  ,
, 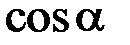 ,
,  – направляющие косинусы вектора, которые находятся по формулам
– направляющие косинусы вектора, которые находятся по формулам .
. в точке
в точке  по направлению
по направлению  .
. определяет величину скорости, а знак производной – характер изменения функции (возрастание или убывание).
определяет величину скорости, а знак производной – характер изменения функции (возрастание или убывание). в точке
в точке  называется вектор, обозначаемый символом
называется вектор, обозначаемый символом  и равный
и равный ,
, от функции
от функции  .
. в точке
в точке  найти градиент и производную по направлению
найти градиент и производную по направлению 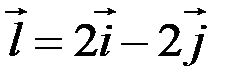 .
. , где
, где тогда
тогда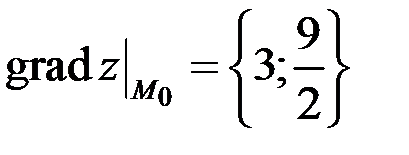 .
. ,
, , тогда
, тогда



