
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Прикладная информатика и математика»Содержание книги
Поиск на нашем сайте
Кафедра «Прикладная информатика и математика» МАТЕМАТИКА
Методические указания по контрольным работам для студентов заочного отделения
Санкт-Петербург
Одобрено на заседании кафедры «Прикладная информатика и математика» протокол № ___ от ________ 2015 г.
Сборник заданий по математике. Методические указания по выполнению контрольных работ по курсу «Математика» для студентов заочного отделения.
Сборник содержит задачи контрольных работ по математике для студентов заочного отделения всех направлений, предусмотренные учебной программой в соответствии с ФГОС ВО. Задания и методические указания могут быть использованы в курсах математических дисциплин всех направлений и специальностей СПб УУиЭ.
Составитель: к.п.н., доцент С.Д. Прозоровская к.э.н. Т.А. Черняк
Рецензент:
Санкт-Петербургский университет управления и экономики
ОГЛАВЛЕНИЕ
1. Требования к оформлению контрольных работ………..……..….…4 2. Формирование исходных данных к задачам………………….…..…4 3. Рекомендуемая литература…………………….……………………..5 4. Контрольная работа № 1. Линейная алгебра……………………..…6 5. Контрольная работа № 2. Элементы векторной алгебры и аналитической геометрии……………………………………………………24 6. Контрольная работа № 3. Предел и производная функции одной переменной……………………………………………………….….35 7. Контрольная работа № 4. Интегральное исчисление функции одной переменной…………………………………………………..….50 8. Контрольная работа № 5 Дифференциальное исчисление функции нескольких переменных……………………………………………57 9. Краткое содержание (программа) курса…………………….…….63
Требования к оформлению контрольных работ 1. Контрольные работы следует выполнять в отдельной тетради. На обложке тетради необходимо указать: название института Университета; название кафедры; название и номер контрольной работы; название (номер) специальности; фамилию,имя, отчество и личный шифр студента. 2. На каждой странице следует оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу. 3. Условия задач переписывать полностью необязательно, достаточно указать номера задач по данному сборнику. В условия задач следует сначала подставить конкретные числовые значения параметров т и п, после чего выполняется их решение.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам Каждая контрольная работа состоит из задач одного или нескольких разделов сборника. Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу. Числовые значения параметров т и п определяются по двум последним цифрам личного шифра (А – предпоследняя цифра, В – последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п – из таблицы 2. Числа т и п следует подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
Таблица 2 (выбор параметра п)
Например, если шифр студента 1604 – 037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 2. Полученные т = 4 и п = 2 подставляются в условия всех задач контрольной работы студента.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие – М.: Высшая школа, 2003. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учебное пособие – М.: Высшее образование, 2006. 3. Высшая математика для экономистов: учебник / под ред. Н. Ш. Кремера. – М.: ЮНИТИ, 2006. 4. Данко, П. Е. Высшая математика в упражнениях и задачах: учеб. Пособие: в 2 ч. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Оникс 21 век, 2005. 5. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс – М.: Айрис-пресс, 2009. 6. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. 2 курс – М.: Айрис-пресс, 2009. 7. Пискунов Н.С. Дифференциальное и интегральное исчисление. Том 1, 2. – М.: Наука, 1988. 8. Письменный, Д. Т. Конспект лекций по высшей математике: в 2 ч. Ч. 1 / Д. Т. Письменный. – М.: Айрис-пресс, 2003.
9. Практикум по высшей математике для экономистов: учебник / под ред. Н. Ш. Кремера. – М.: ЮНИТИ, 2004. Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
Матрицы и действия над ними Прямоугольная таблица чисел вида
называется матрицей размера m ´ n; здесь m – число строк, n – число столбцов. Числа Если число строк и столбцов матрицы одинаковое Квадратная матрица, в которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной, а диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице, называется единичной:
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Например:
Матрица, все элементы которой равны нулю, называется нулевой и обозначается символом О, например Прямоугольная матрица, в которой каждая строка заменена столбцом с тем же номером, называется транспонированной по отношению к данной матрице, обозначается Очевидно, что Действия над матрицами
Две матрицы одинакового размера называются равными, если их соответствующие элементы равны. А = В, если Суммой двух матриц одинакового размера называется матрица того же размера, все элементы которой равны суммам соответствующих элементов слагаемых матриц. А + В = С, если
Пример 1
Произведением матрицы А на число α называется матрица αА или А α, все элементы которой равны соответствующим элементам матрицы А, умноженным на α.
Пример 2
Матрица
Умножение матриц.
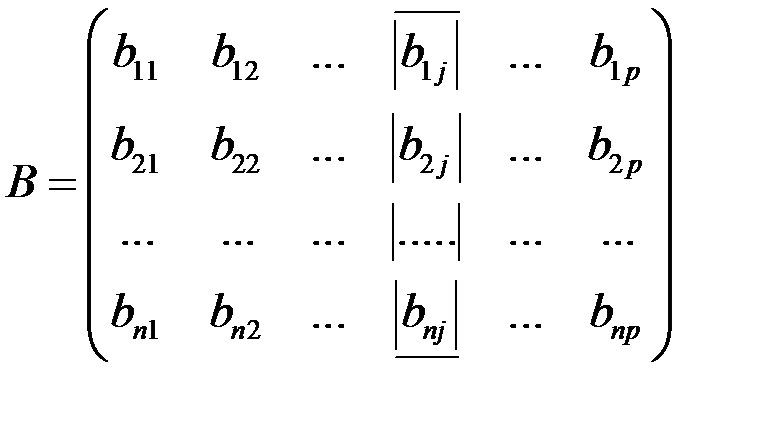
Пусть дана матрица А размера m ´ n и матрица В размера n ´ p.
Для двух матриц А и В, у которых число столбцов первой матрицы равно числу строк второй матрицы, определено понятие произведения матрицы А на В следующим образом: С = А · В, где С есть матрица размера m ´ p,
если
Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i -той строке и j -том столбце произведения двух матриц, нужно элементы i -той строки первой матрицы умножить на соответствующие элементы j –го столбца второй и полученные произведения сложить. Таким образом, чтобы составить первую строку матрицы С нужно перемножить первую строку матрицы А поочередно на все столбцы В; чтобы получить вторую строку произведения С, нужно вторую строку А перемножить последовательно на все столбцы В и т.д. Пример 3
Произведение двух матриц НЕ подчиняется переместительному (коммутативному) закону
в чем можно убедиться на примерах. Кроме того, если произведение АВ определено, то ВА может не иметь смысла. В частных случаях, когда Легко доказать, что единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем А Е = Е А = А. Таким образом, единичная матрица играет роль единицы при умножении. Пример 4 Найти значение матричного многочлена
Решение
Пример 3 Вычислить определитель по правилу треугольника: Решение
Свойства определителей
Рассмотрим свойства определителей на примере определителя 3-го порядка. Рассмотрим определитель:
Определение. Минором некоторого элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пресечении которых стоит этот элемент. Обозначение минора Пример 4 Минор элемента а12:
Определение. Алгебраическим дополнением любого элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, есть число четное, либо с противоположным знаком, если эта сумма есть число нечетное. Обозначение алгебраического дополнения Аij. Пример 5
Свойство 1. Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.
Пример 6 Вычислим определитель, разложив его по элементам 1-ой строки:
Свойство 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.
Свойство 3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).
Свойство 4. Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя. Свойство 5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю. Свойство 6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю. Свойство 7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.
Свойство 8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые:
Свойство 9. Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится. Пример 7 Вычислим определитель:
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
Обратная матрица
Пусть дана квадратная матрица А порядка n. Обратной матрицей по отношению к данной А называется матрица По определению А · Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной. Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
где
для квадратной матрицы 3-го порядка союзной является матрица
Пример Для матрицы Решение Обратную матрицу находим по формуле
Определитель матрицы
Тогда обратная матрица имеет вид
Пример 1. Решить систему Решение Формулы Крамера:
Итак, Ранг матрицы
Пусть дана матрица
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Обозначение: rang A, r (А) или r. Очевидно, Минор, порядок которого определяет ранг матрицы, называется базисным. Вычисление всех миноров отличных от нуля трудоемкая операция. На практике для вычисления r (A) используют метод Гаусса. Элементарными преобразованиями называются следующие действия над матрицами: 1. Вычеркивание нулевой строки. 2. Умножение какой либо строки на число. 3. Прибавление к одной из строк другой строки, умноженной на любое число. 4. Перестановка двух столбцов или двух строк.
Теорема 1. Ранг матрицы не меняется при элементарных преобразованиях.
Пример 2. Найти ранг матрицы Решение
На первом шаге первую строку матрицы умножили на (-2) и сложили со второй строкой, умножили первую строку на (-4) и сложили с третьей строкой. На втором шаге вторую строку умножили на (-3) и сложили с третьей строкой. Нулевую строку вычеркнули. Таким образом, ранг матрицы r = 2.
Метод Гаусса решения СЛАУр Пусть дана система линейных алгебраических уравнений (СЛАУр)
Поставим задачу: исследовать данную систему, т.е. выяснить, не решая ее, совместна она или несовместна, а если совместна, то определенна она или неопределенна. На все эти вопросы отвечает теорема Кронекера - Капелли. Пусть дана матрица системы Рассмотрим расширенную матрицу системы
Теорема Кронекера – Капелли. СЛАУр совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы:
Замечание Если Метод Гаусса решения СЛАУр состоит в следующем.
1. Выписывают расширенную матрицу системы
и с помощью элементарных преобразований приводят ее к трапециевидному виду. 2. Применяя теорему Кронекера – Капелли, исследуют систему, получая один из случаев: – система совместна и определенна, – система совместна и неопределенна, – система несовместна. Трапециевидная форма расширенной матрицы С в каждом из этих случаев имеет вид:
1) С ~ следовательно, система определенна, имеет единственное решение,
2) С ~ следовательно, система неопределенна, имеет бесконечное множество решений,
3) если какая-либо строка матрицы С имеет вид
3. Для решения системы, если оно существует, следует записать новую систему, отвечающую полученной трапециевидной матрице, которая является более простой по сравнению с исходной и решить ее (обратный ход).
Пример 3. Исследовать и решить СЛАУр: Решение Составим расширенную матрицу и проведем над ней эквивалентные преобразования для определения
Таким образом, Составим систему, соответствующую последней матрице, эквивалентную исходной:
Таким образом,
Пример 4. Исследовать и решить СЛАУр: Решение
Так как Последней матрице соответствует система:
где
Пример 5. Исследовать и решить СЛАУр: Решение
Так как
Пример 6. Исследовать и решить СЛАУр: Решение
Таким образом, Прямая на плоскости Уравнение вида
называется общим уравнением прямой. Уравнение вида
называется уравнением прямой с угловым коэффициентов, здесь
Пусть даны две точки прямой
Уравнение прямой, проходящей через заданную точку
Пример Даны вершины треугольника 1) уравнение стороны АВ; 2) уравнение медианы, проведенной из вершины С; 3) координату точки пересечения медиан; 4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину; 5) уравнение прямой, проходящей через точку С параллельно прямой АВ; 6) площадь треугольника. Решение 1) Используем уравнение прямой, проходящей через две точки
2) Медиана, проведенная из вершины С делит противолежащую сторону АВ треугольника пополам. Найдем координаты точки Е середины стороны
3) Точка М делит каждую медиану в отношении
В нашем случае
откуда 4) Найдем уравнение прямой, проходящей через заданную точку
Угловой коэффициент прямой АС равен
Длину высоты можно найти, как расстояние от точки
5) Для нахождения уравнения прямой, проходящей через точку С параллельно прямой АВ используем уравнение прямой, проходящей через заданную точку в заданном направлении
- уравнение искомой прямой. 6) Площадь треугольника находится по формуле:
у А (4;6)
Е
В (-4;0) М 0 1 х
С (-1;-4) Рис. 1 Пример Даны вершины треугольной пирамиды 1) угол между ребрами 2) площадь грани 3) объем пирамиды 4) длину высоты, опущенной из вершины 5) угол между ребром 6) уравнение высоты, опущенной из вершины
Решение
2) Площадь грани
Найдем векторное произведение векторов
модуль векторного произведения равен
откуда находим площадь треугольника
3) Объем пирамиды находим с помощью смешанного произведения векторов по формуле
так как выше найдены координаты векторов
подставим координаты векторов в формулу, получим
4) Для нахождения длины высоты h, опущенной из вершины
откуда находим
5) Общее уравнение плоскости
нормальный вектор плоскости Уравнение высоты Условие перпендикулярности прямой и плоскости: В нашем случае
Пример 1
так как при Пример 2
Пример 3
Замечание. Из рассмотренных примеров видно, что предел частного двух многочленов при 3.2. Раскрытие неопределенности вида Рассмотрим отношение функций Чтобы раскрыть неопределенность вида Чтобы раскрыть неопределенность вида
Пример Вычислить предел Решение При
тогда,
Таким образом, получим:
Пример Вычислить предел
Решение Предел основания
и применим второй замечательный предел:
Непрерывность функции
Пусть функция Определение. Функция
Таким образом, для того чтобы функция 1) функция 2) должны сущест
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.38.137 (0.013 с.) |


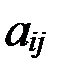 (i = 1,2,…, m; j = 1,2,…, n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.
(i = 1,2,…, m; j = 1,2,…, n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.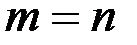 , то матрица называется квадратной, порядка n.
, то матрица называется квадратной, порядка n.
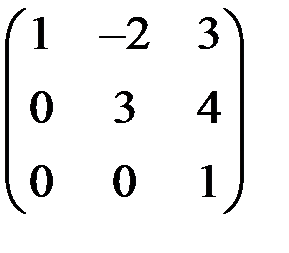 .
. .
.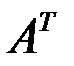 . Например, если
. Например, если  , то
, то 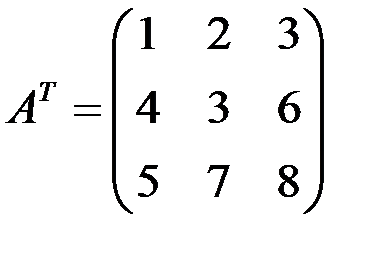 .
.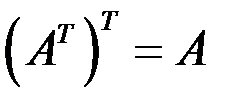 .
. (i = 1,2,…, m; j = 1,2,…, n).
(i = 1,2,…, m; j = 1,2,…, n).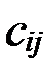 (i = 1,2,…, m; j = 1,2,…, n).
(i = 1,2,…, m; j = 1,2,…, n).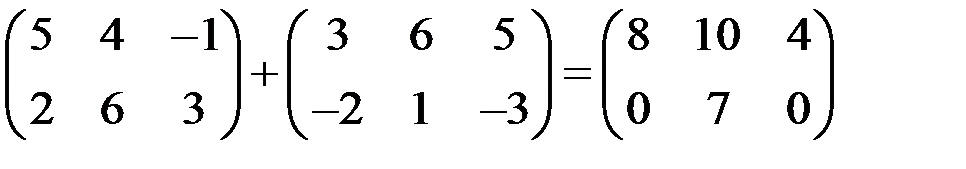 .
.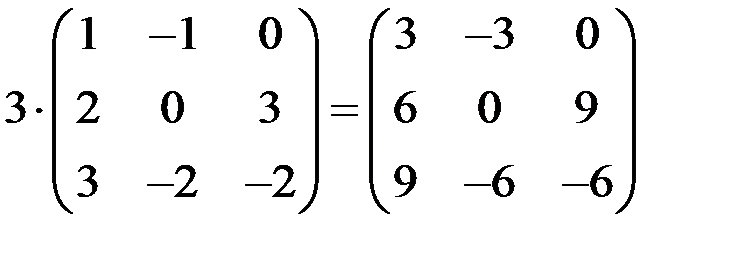
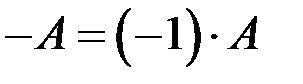 называется противоположной матрице А.
называется противоположной матрице А.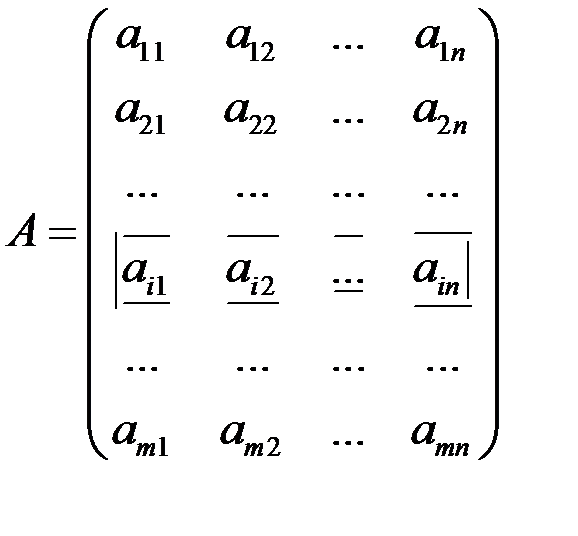

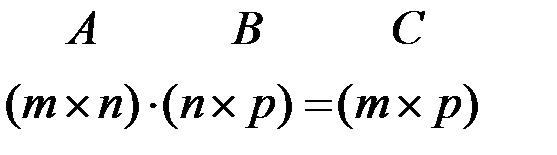 ,
, , где (i = 1,2,…, m; j = 1,2,…, p).
, где (i = 1,2,…, m; j = 1,2,…, p).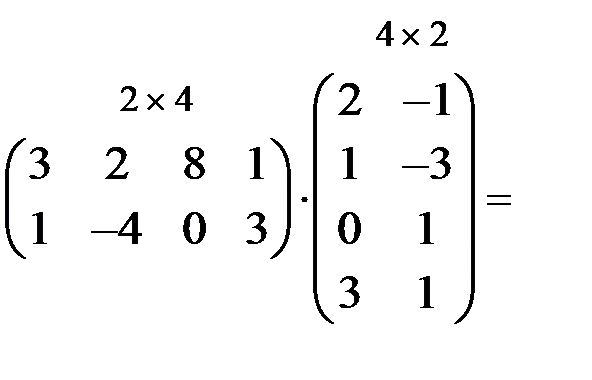

 ,
,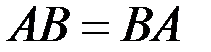 матрицы называются перестановочными.
матрицы называются перестановочными.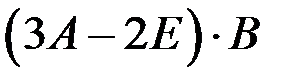 , если
, если 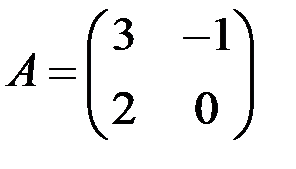 ,
, 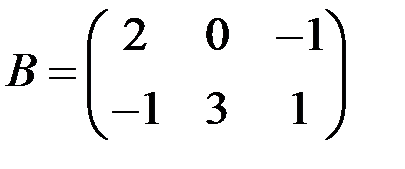 ,
, 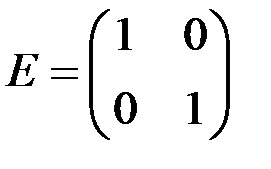 .
.
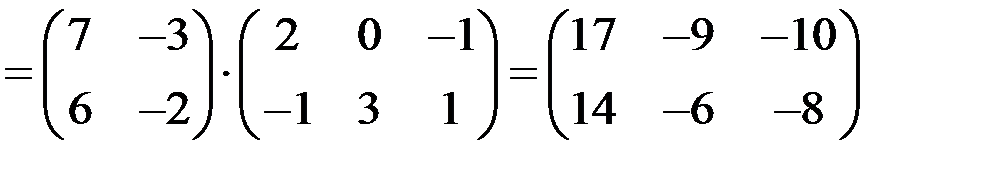 .
. .
.
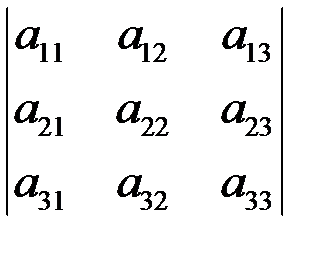 .
.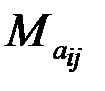 .
. .
.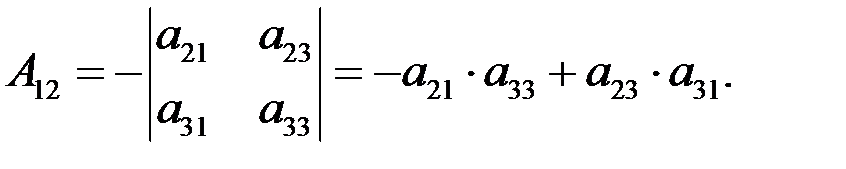
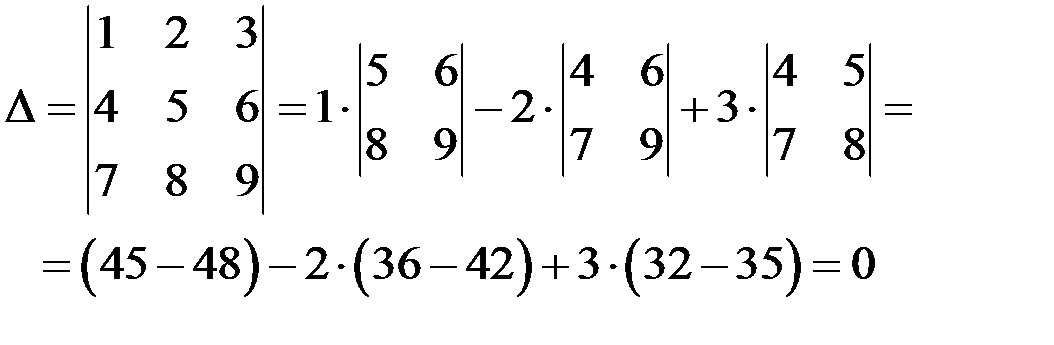 .
.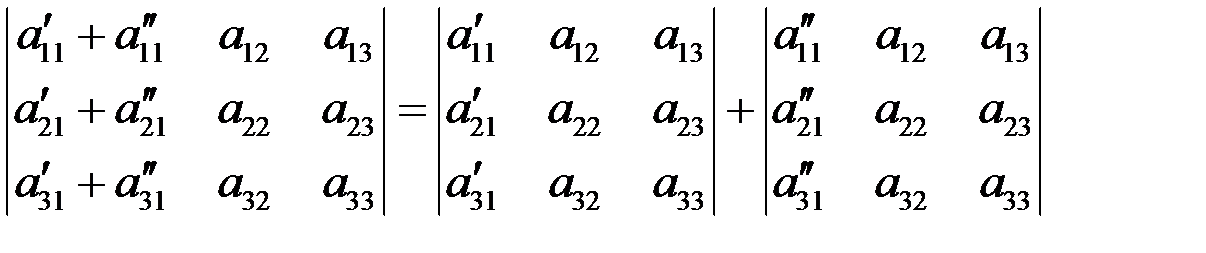 .
. ,
,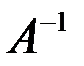 , которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.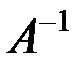 =
= 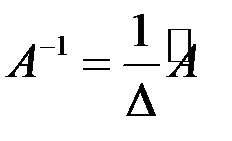 ,
, - определитель матрицы А,
- определитель матрицы А, 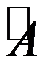 - союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
- союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица ,
,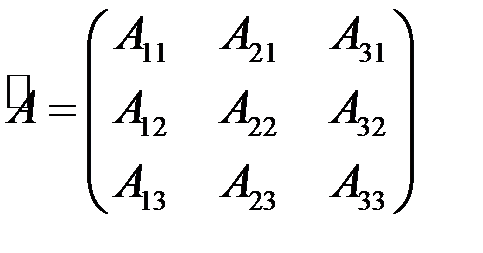 .
.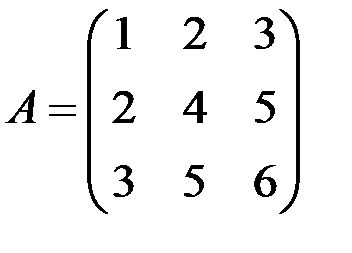 найти обратную.
найти обратную.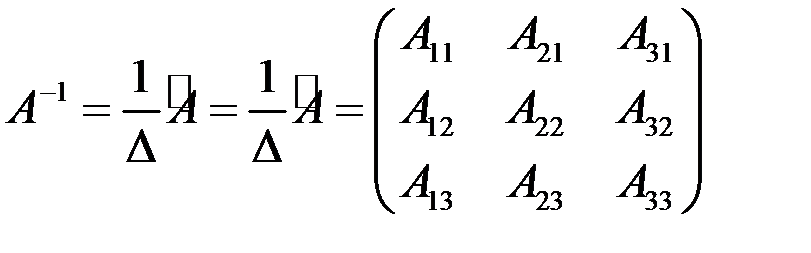 .
. , следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы: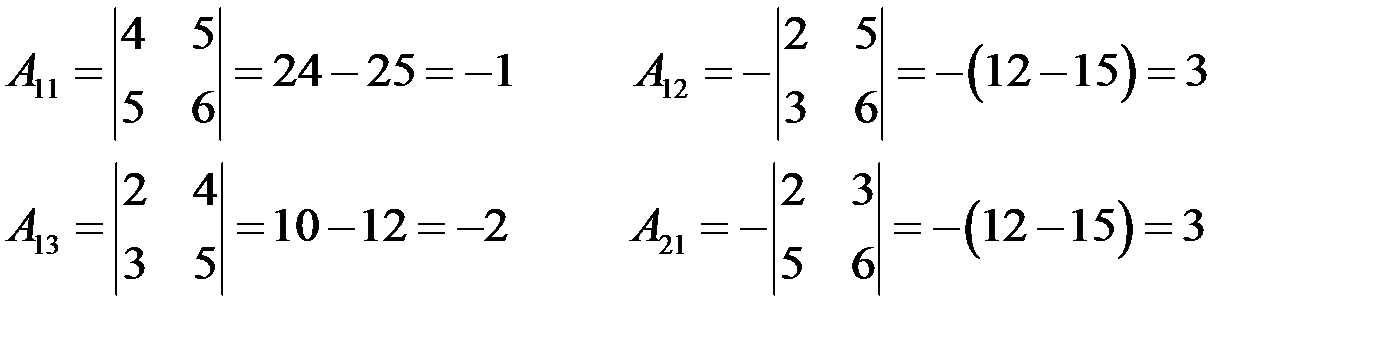


 .
.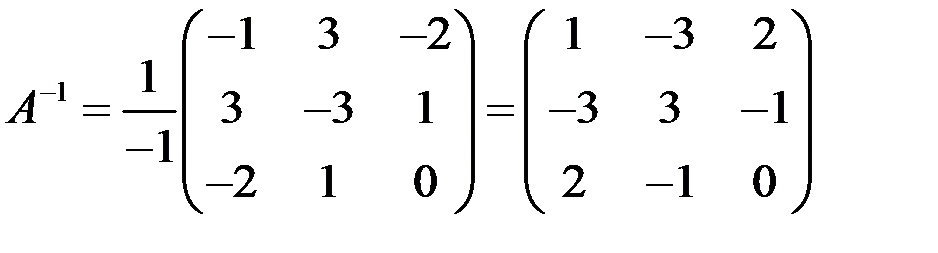 .
. по формулам Крамера.
по формулам Крамера. . Вычислим определители:
. Вычислим определители: ,
, , тогда
, тогда ,
,  ,
,  .
.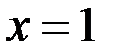 ,
,  ,
,  .
.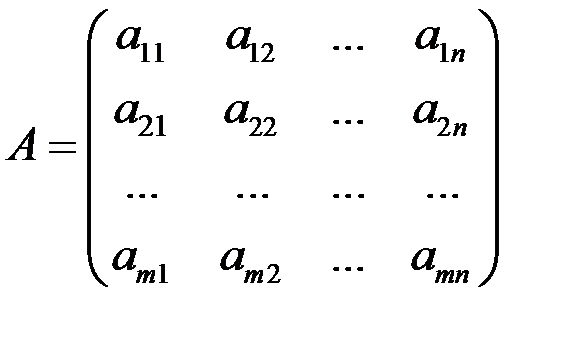 .
. – меньшее из чисел m и n.
– меньшее из чисел m и n. .
. ~
~  ~
~ 

 .
. .
. или
или  .
. и
и  , где n – число неизвестных, то система определенна; если
, где n – число неизвестных, то система определенна; если  , то система неопределенна, если же
, то система неопределенна, если же 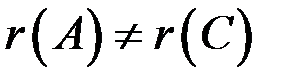 , то система несовместна.
, то система несовместна.

 ,
,  ,
,
 ,
, , то система несовместна (решений нет).
, то система несовместна (решений нет). .
. и
и  .
. ~
~  ~
~ ~
~  ,
,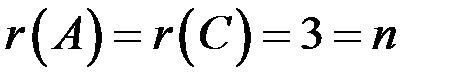 , следовательно, по теореме Кронекера – Капелли система совместна и определенна.
, следовательно, по теореме Кронекера – Капелли система совместна и определенна.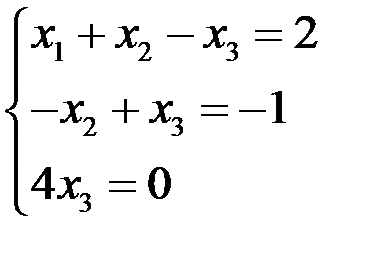 Þ
Þ  .
. .
. .
. ~
~  ~
~ 
 , следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
, следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).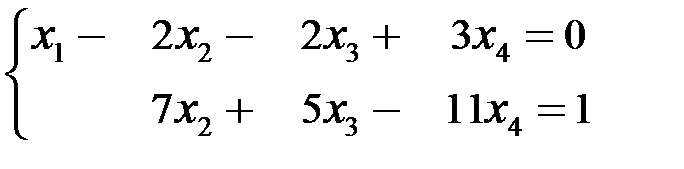 Þ
Þ 
 и
и  – произвольные параметры.
– произвольные параметры.
 ~
~  ~
~ 
 , то система несовместна (решений нет).
, то система несовместна (решений нет). .
.
 .
.

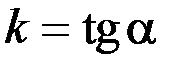 ,
,  - угол, образованный прямой с положительным направлением оси Ох, b – ордината точки пересечения прямой с осью Оу.
- угол, образованный прямой с положительным направлением оси Ох, b – ордината точки пересечения прямой с осью Оу. и
и  . Уравнение прямой, проходящей через две заданные точки имеет вид
. Уравнение прямой, проходящей через две заданные точки имеет вид .
.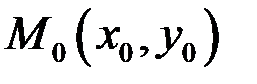 в заданном направлении, определяемом угловым коэффициентом k, имеет вид
в заданном направлении, определяемом угловым коэффициентом k, имеет вид .
. . Найти:
. Найти: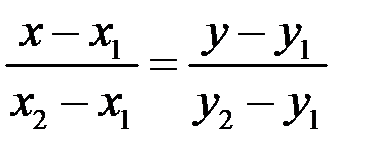 . Подставив координаты точек
. Подставив координаты точек 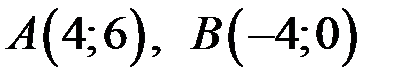 , получим
, получим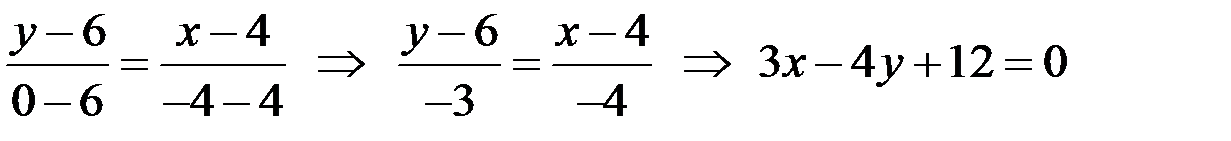 - общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом
- общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом  ,
,  .
. (рис.1):
(рис.1): , т.е.
, т.е.  ,
,  . Подставим координаты точек в уравнение прямой, проходящей через две точки, получим
. Подставим координаты точек в уравнение прямой, проходящей через две точки, получим  - общее уравнение прямой СЕ.
- общее уравнение прямой СЕ. , считая от вершины. Таким образом, ее координаты
, считая от вершины. Таким образом, ее координаты  можно найти по формулам:
можно найти по формулам: .
. ,
, .
. перпендикулярно прямой
перпендикулярно прямой  из уравнения
из уравнения  . Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки
. Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки  и
и  :
: - уравнение АС.
- уравнение АС. , тогда, используя условие перпендикулярности двух прямых
, тогда, используя условие перпендикулярности двух прямых  , получим
, получим - уравнение высоты.
- уравнение высоты. до прямой АС по формуле
до прямой АС по формуле  . В нашем случае уравнение прямой АС:
. В нашем случае уравнение прямой АС:  , следовательно,
, следовательно, .
. и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен
и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен  , следовательно,
, следовательно, -
- , в нашем случае
, в нашем случае .
.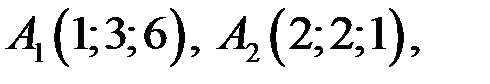
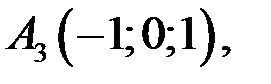
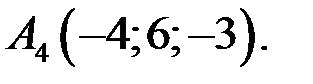 Найти:
Найти: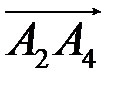 и
и 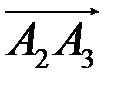 ;
; ;
;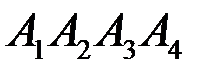 ;
; на грань
на грань 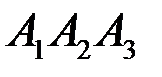 ;
;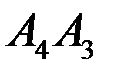 и гранью
и гранью 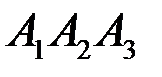 ;
;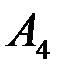 на грань
на грань 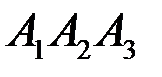 .
.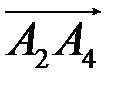 и
и 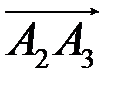 находим с помощью скалярного произведения векторов по формуле
находим с помощью скалярного произведения векторов по формуле
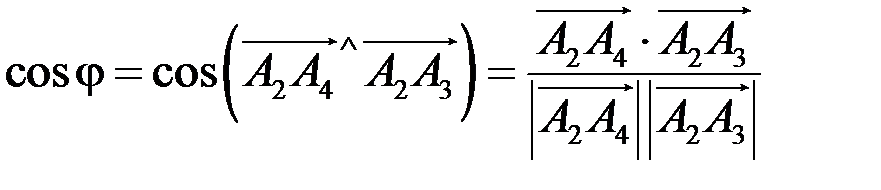 ,
найдем координаты векторов
,
найдем координаты векторов
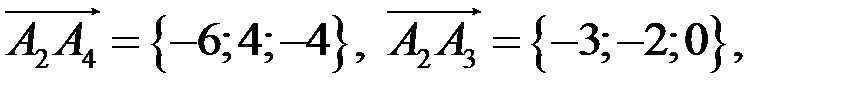 тогда косинус угла между векторами
тогда косинус угла между векторами
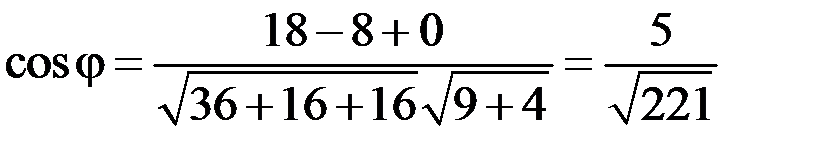 .
.
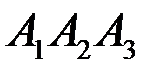 находим с помощью векторного произведения векторов. Найдем координаты вектора
находим с помощью векторного произведения векторов. Найдем координаты вектора 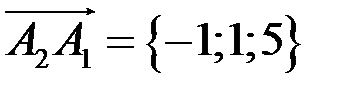 , тогда площадь треугольника находим по формуле
, тогда площадь треугольника находим по формуле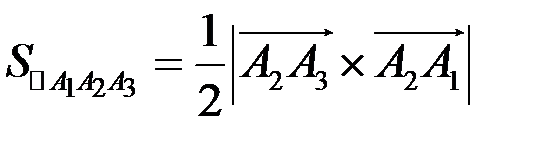 .
.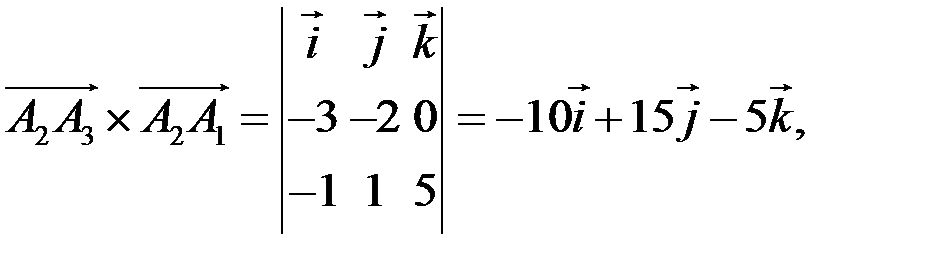
 ,
,
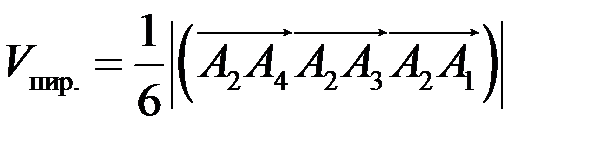 ,
,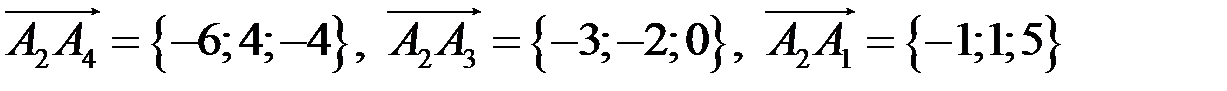 ,
,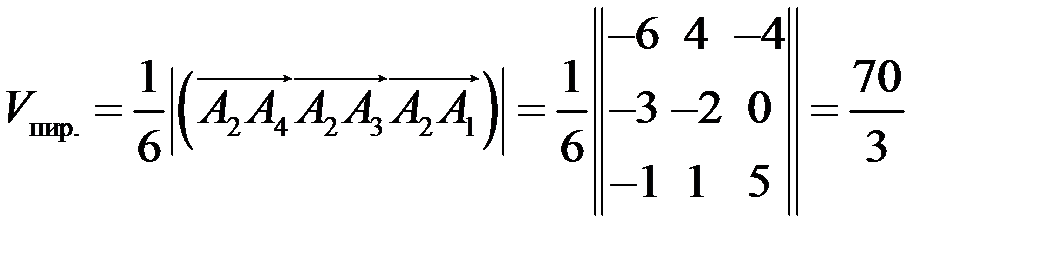 .
.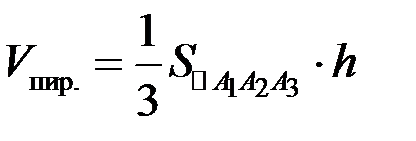 ,
,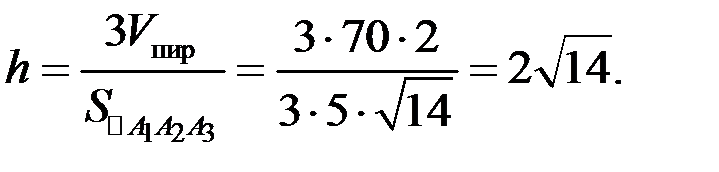
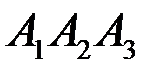 :
: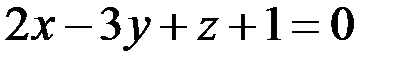 ,
,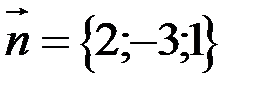 .
.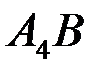 :
: 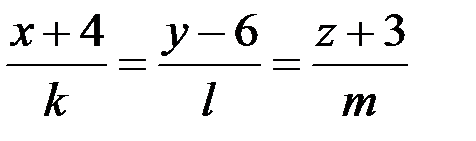 .
.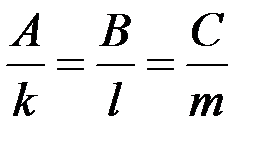 .
. , тогда уравнение высоты имеет вид
, тогда уравнение высоты имеет вид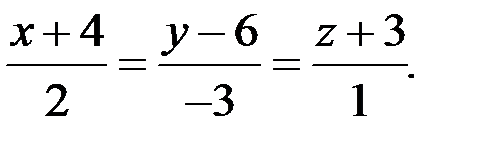
 ,
, каждая из дробей
каждая из дробей  стремится к нулю.
стремится к нулю. .
. .
.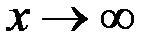 равен отношению коэффициентов при старших членах, если степени многочленов, стоящих в числителе и знаменателе, равны; равен нулю, если степень числителя меньше степени знаменателя; равен ¥, если степень числителя больше степени знаменателя.
равен отношению коэффициентов при старших членах, если степени многочленов, стоящих в числителе и знаменателе, равны; равен нулю, если степень числителя меньше степени знаменателя; равен ¥, если степень числителя больше степени знаменателя.
 . Пусть
. Пусть  – бесконечно малые функции (б.м.ф.) при
– бесконечно малые функции (б.м.ф.) при  , отношение
, отношение 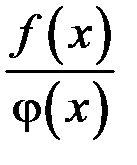 в этом случае называется неопределенным выражением вида
в этом случае называется неопределенным выражением вида 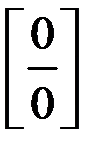 .
. , заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель и сократить на него.
, заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель и сократить на него. , в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности, домножив числитель и знаменатель на сопряженное выражение.
, в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности, домножив числитель и знаменатель на сопряженное выражение. .
. числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида
числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида  , а квадратный трехчлен
, а квадратный трехчлен  разложим на множители, найдя для этого его корни:
разложим на множители, найдя для этого его корни: ,
, .
.


 .
. .
. , а показатель степени
, а показатель степени  при
при  , т.е. имеет место неопределенность вида
, т.е. имеет место неопределенность вида  . Выделим целую часть основания степени
. Выделим целую часть основания степени

 , учитывая, что
, учитывая, что  .
.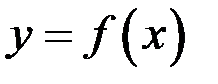 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
. называется непрерывной в точке
называется непрерывной в точке  , если она имеет предел в точке
, если она имеет предел в точке  и этот предел равен
и этот предел равен  – значению функции
– значению функции 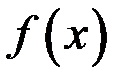 в точке
в точке  :
: .
.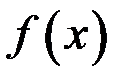 была непрерывна в точке
была непрерывна в точке  , необходимо и достаточно выполнение трех условий:
, необходимо и достаточно выполнение трех условий: должна быть определена в точке
должна быть определена в точке  ;
;


