
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 4. Интегральное исчисление функции одной переменной
5.1. Найти интеграл 5.2. Найти интеграл 5.3. Найти интеграл 5.4. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
Метод интегрирования подведением под знак дифференциала
Функция Совокупность всех первообразных для функции
Метод подведения под знак дифференциала следует из свойства инвариантности неопределенного интеграла. Пусть дан интеграл
где
Таблица интегралов
При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:
В общем случае
Пример 1 Найти интеграл Так как
Пример 2 Найти интеграл Так как
Пример 3 Найти интеграл Так как
Пример 4 Найти интеграл Так как
Метод интегрирования по частям
Пусть дан интеграл вида
Таким образом, вычисление интеграла Пусть
Пример Найти интеграл Решение Положим
Интегрирование тригонометрических выражений
Рассмотрим интеграл вида Универсальная подстановка
Итак:
Пример
Найти интеграл Решение Применим универсальную подстановку
получим
Вычисление площадей с помощью определенного интеграла
Пусть функция Разобьем отрезок Обозначим Обозначим длину наибольшего частичного промежутка через
Если существует конечный предел
Если
т.е. для вычисления определенного интеграла от непрерывной функции
Пример 1
Если
прямыми
Если
Пусть нужно вычислить площадь фигуры, ограниченной кривыми
Пример 2 Вычислить площадь фигуры, ограниченной линиями Решение
Контрольная работа № 5. Дифференциальное исчисление функции нескольких переменных. 5.1. Найти дифференциал 5.2. Показать, что функция 5.3. Составить уравнения касательной плоскости и нормали к поверхности 5.4. Для функции
Краткие теоретические сведения для выполнения контрольной работы № 5 и решение типовых задач
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.02 с.) |
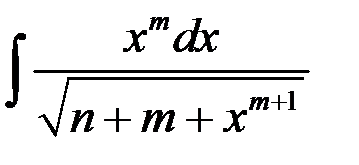 .
. .
.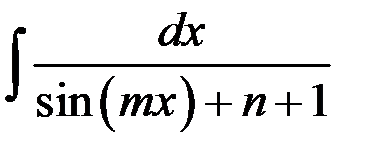 .
. ,
,  .
. называется первообразной для функции
называется первообразной для функции  на интервале
на интервале  , конечном или бесконечном, если в любой точке
, конечном или бесконечном, если в любой точке  этого интервала функция
этого интервала функция  дифференцируема и имеет производную
дифференцируема и имеет производную  .
. , определенных на интервале
, определенных на интервале  , называется неопределенным интегралом от функции
, называется неопределенным интегралом от функции 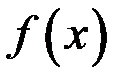 на этом интервале и обозначается символом
на этом интервале и обозначается символом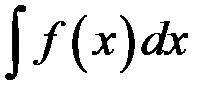 .
.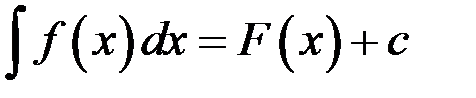 . Справедливо равенство
. Справедливо равенство ,
, – некоторая непрерывно дифференцируемая функция.
– некоторая непрерывно дифференцируемая функция.











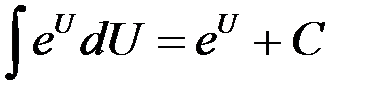





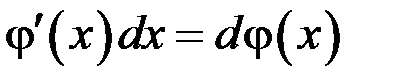 .
. .
. , то
, то .
. .
. , то
, то .
. .
. , то
, то
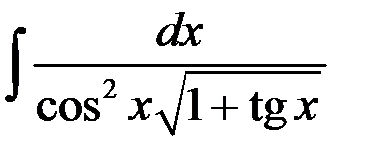 .
. , то
, то .
. , где
, где  - непрерывно дифференцируемые функции. Справедлива формула интегрирования по частям
- непрерывно дифференцируемые функции. Справедлива формула интегрирования по частям .
. приводится к вычислению интеграла
приводится к вычислению интеграла 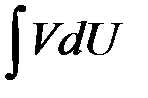 , который может оказаться более простым или табличным.
, который может оказаться более простым или табличным. - многочлен степени n. Методом интегрирования по частям можно вычислить, например, интегралы вида:
- многочлен степени n. Методом интегрирования по частям можно вычислить, например, интегралы вида:


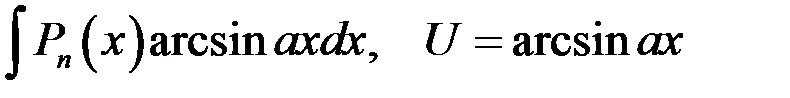

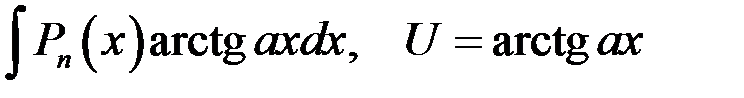


 .
. , найдем
, найдем 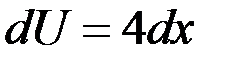 ,
,  . Так как достаточно взять одну из первообразных, то принимаем
. Так как достаточно взять одну из первообразных, то принимаем  . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям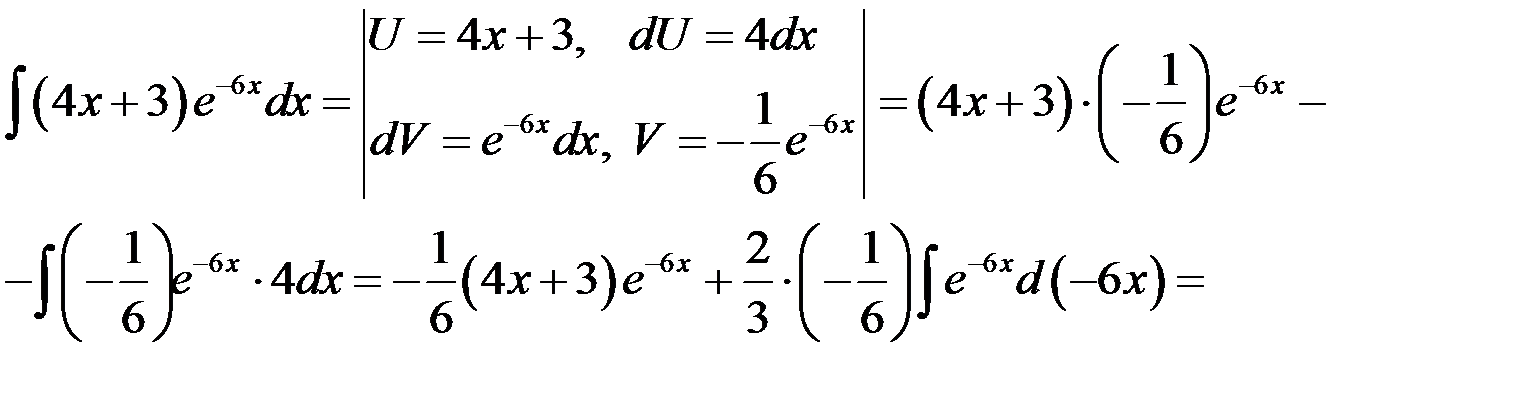
 .
. где R – рациональная функция своих аргументов.
где R – рациональная функция своих аргументов. сводит данный интеграл к интегралу от рациональной дроби, при этом
сводит данный интеграл к интегралу от рациональной дроби, при этом ,
, 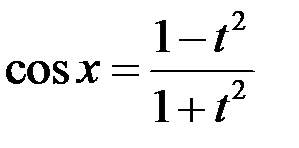 ,
,  .
.
 .
. ,
,

 определена и непрерывная на отрезке
определена и непрерывная на отрезке  и пусть, для определенности,
и пусть, для определенности, 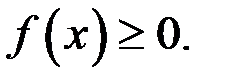
 на n частей произвольным образом точками деления:
на n частей произвольным образом точками деления:  . Выберем на каждом частичном промежутке
. Выберем на каждом частичном промежутке  произвольным образом точки
произвольным образом точки 
 .
. Составим сумму
Составим сумму  , которая называется интегральной суммой для функции
, которая называется интегральной суммой для функции  на отрезке
на отрезке 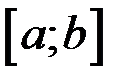 .
. Перейдем к пределу при
Перейдем к пределу при  .
. , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка  на частичные и выбора на них точек
на частичные и выбора на них точек 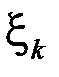 , то он и называется определенным интегралом от функции
, то он и называется определенным интегралом от функции  на отрезке
на отрезке  и обозначается
и обозначается
 – любая первообразная для функции
– любая первообразная для функции  , то справедлива формула Ньютона – Лейбница:
, то справедлива формула Ньютона – Лейбница: ,
,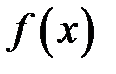 нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
 то
то  численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 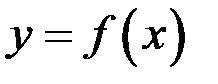 ,
, и осью ох:
и осью ох:
 меняет знак конечное число раз на отрезке
меняет знак конечное число раз на отрезке  , то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где
, то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где  и отрицателен, где
и отрицателен, где  :
: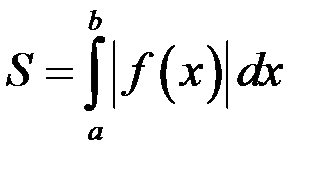 .
. и
и  и прямыми
и прямыми  , тогда при условии
, тогда при условии 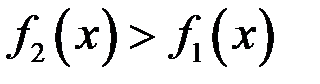 имеем
имеем
 и
и  .
. ,
, 


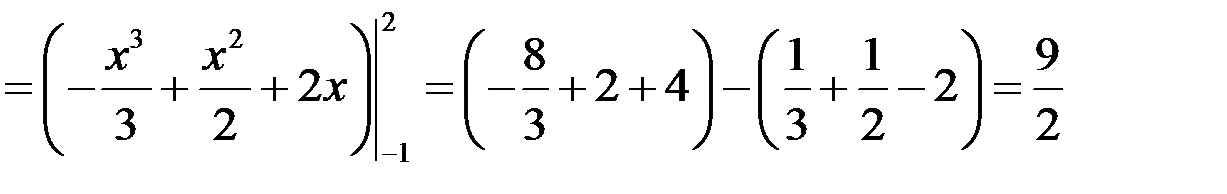 .
. функции
функции  .
. удовлетворяет уравнению
удовлетворяет уравнению  .
. в точке
в точке  .
. в точке
в точке  найти градиент и производную по направлению
найти градиент и производную по направлению 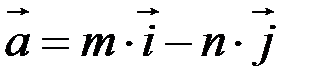 .
.


