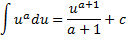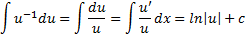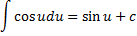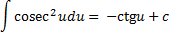Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение производной. Общее правило нахождения производной.
Определение производной. Общее правило нахождения производной. Производная – придел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0
Общее правило: находим Правила и формулы дифференцирования элементарных функций. Дифференцирование – это взятие производной от функции. Правила дифференцирования: 1)производная постоянной равна нулю (c)ʹ = 0, c - const 2)производная Х равна 1 (x)ʹ = 1 3) постоянный множитель выносится за знак производной (c*u)ʹ=c*uʹ, c - const 4) производная алгебраической суммы функции равна алгебраической сумме производных от каждого слагаемого (u+γ-ω) ʹ= uʹ+γʹ-ωʹ 5) производная произведения равна производной первого множителя на второй, плюс производная второго множителя, умноженного на первый (u*γ) ʹ= uʹγ+ γʹu 6) производная частного равна производной числителя умноженного на знаменатель, минус производная знаменателя, умноженная на числитель и делить на знаменатель в квадрате
Формулы дифференцирования:
Дифференцирование логарифмической функции. Производная показательной функции.
Дифференцирование тригонометрических функций и обратных тригонометрических функций. см 2 билет (косинусы, синусы, тангенсы, катангенсы, арккосинусы, арксинусы, арктангенсы)
Производная второго порядка и её механический смысл. Уравнение касательной. Производную от функции часто называют производной первого порядка (первой производной). Очевидно, что производная также является функцией и если она дифференцируема, то от нее в свою очередь можно взять производную, которую называют производной второго порядка (второй производной) и обозначают yʹʹ,
Пусть тело движется прямолинейно по закону S=f(t). Как известно, скорость U движения тела в данный момент времени равно производной пути по времени, т.е. U=S Если тело движется неравномерно, то скорость с течением времени изменяется и за промежуток времени В этом случае величина отношения Пусть
Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента. Уравнение касательной:
y=f(x)
Понятие дифференциала. Геометрический смысл дифференциала. Вычисление дифференциала. Дифференциал – главная часть приращения функции, линейная относительно приращения независимой переменной, обозначается знаком d т.е. Геометрический смысл: дифференциал функции дифференциал можно вычислить по формуле
Понятие первообразной. Определение неопределенного интеграла и его свойства. Дифференцируемая функция F(x), где Совокупность всех первообразных функции f(x) на интервале от Свойства неопределенного интеграла: 1) постоянный множитель выносится за знак интеграла 2) интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от каждого из слагаемых
Формулы интегрирования. Вычисление неопределенного интеграла. Пример.
Тут надо придумать. Можно что-то простое
Основные понятия стереометрии. Аксиомы стереометрии. Их следствия. Взаимное расположение двух прямых в пространстве. Стереометрия – это раздел геометрии, в котором фигуры изучаются в пространстве.
Основные фигуры: точка, прямая, плоскость. Аксиомы: 1. Какова бы ни была плоскость, существуют точки принадлежащие и не принадлежащие ей. 2. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящую через эту точку. 3. Через две пересекающиеся прямые можно провести плоскость, и притом только одну. Следствия из них: 1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Доказательство: возьмем точку принадлежащую прямой. Через две точки проведем прямую, назовем b. Имея две пересекающиеся прямые по аксиоме мы может провести плоскость и притом только одну. 2. Если две точки прямой принадлежат плоскости, то и сама прямая принадлежит этой плоскости. Доказательство: пусть a – данная прямая и α - данная плоскость. Проведем через прямую a и точку A плоскость α`. Если плоскость α` совпадает с α, то плоскость α содержит прямую a, что и утверждается теоремой. Если плоскость α` отлична от α, то эти плоскости пересекаются по прямой a`, содержащей две точки прямой a. 3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну. Взаимное расположение двух прямых в пространстве: Прямые, лежащие на одной плоскости, имеющих одну общую точку,называют пересекающимися. Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек. Прямые называются скрещивающимися, если они лежат в разных плоскостях.
Определение производной. Общее правило нахождения производной. Производная – придел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0
Общее правило: находим
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.187 (0.009 с.) |

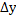 , потом
, потом  и затем обношение
и затем обношение 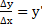



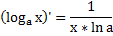


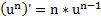 *uʹ
*uʹ
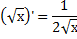

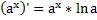

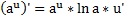



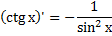
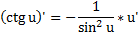
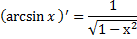
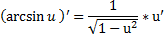
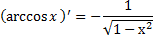
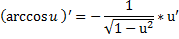
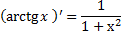



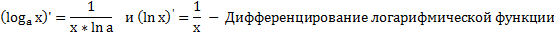
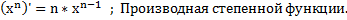
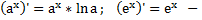 Производная показательной функции.
Производная показательной функции.
 получает приращение
получает приращение 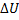
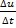 показывающаяся изменение скорости за единицу времени, называется средним ускорением в промежутке времени от t до t+
показывающаяся изменение скорости за единицу времени, называется средним ускорением в промежутке времени от t до t+  , тогда t+
, тогда t+  , а среднее ускорение
, а среднее ускорение 
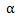

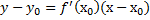

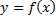 геометрический изображается приращением ординаты касательной, проведенной в точке М(x;y) при данных значениях x и
геометрический изображается приращением ординаты касательной, проведенной в точке М(x;y) при данных значениях x и 

 называется первообразной для f(x), где
называется первообразной для f(x), где 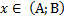 , если выполняется равенство:
, если выполняется равенство: 
 Называется неопределенным интегралом f(x) и обозначается
Называется неопределенным интегралом f(x) и обозначается 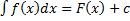
 , с-const
, с-const