Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные функций двух переменных.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим функцию двух переменных z = f(x, y). Частной производной функции двух переменных z = f(x, y) по х в точке (х, у) называется предел Аналогично определяется частная производная по у в точке (х,у):
Если у функции Аналогично для переменной у: Если существует частная производная от функции В курсе высшей математики доказывается теорема о том, что если функция двух переменных определена вместе со своими частными производными в окрестности некоторой точки, причем смешанные частные производные непрерывны в этой точке, то в этом случае результат дифференцирования не зависит от порядка дифференцирования, т. е. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ Рассмотрим функцию двух переменных z = f(x, y). Если эта функция дифференцируема в точке (х,у), то для нее существует производная по направлению любого единичного вектора ` n0 = (Cosa, Cosb), выражаемая формулой где a и b - углы, которые вектор ` n0 составляет с осями х и у. Если же необходимо найти производную по направлению произвольного вектора ` n = a`i + в`j, то его необходимо сначала пронормировать и найти направляющие косинусы по формулам ГРАДИЕНТ ФУНКЦИИ Градиентом функции z = f(x, y) в точке М(х0, у0) называется вектор grad z, координаты которого равны частным производным функции z = f(x, y), вычисленным в точке М(х0, у0)
ЗАДАЧА № 9 Найти частные производные
ЗАДАЧА № 10 Найти градиент и производную по направлению
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ При изучении дифференцированного исчисления решалась следующая задача: дана функция F(x), найти ее производную F¢(x) (в дальнейшем производную F¢(x) будем обозначать f(x)). Интегральное исчисление решает задачу обратную: для непрерывной функции f(x) найти такую функцию F(x), производная которой была бы тождественно равна функции f(x). Функция F(x) называется первообразной, f(x) - подынтегральной. Ясно, что если F¢(x) = f(x), то и [F¢(x) + C]¢ = f(x). Здесь С - произвольная постоянная величина. Определение: Неопределенным интегралом
Подынтегральное выражение f(x)dx есть дифференциал для всех первообразных, т.е. d[F(x) + C] = f(x)dx. Из определения следует, что процесс нахождения неопределенного интеграла сводится к нахождению первообразной данной функции. Вообще, используя таблицу производных, можно составить таблицу основных интегралов:
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 1. 2. 3. ЗАДАЧА № 11 Найти неопределенный интеграл
МЕТОД ПОДСТАНОВКИ Метод заключается в том, что вместо переменной x вводят новую переменную, например t. Так, если положить х = j(t), то
ЗАДАЧА № 12 Найти неопределенный интеграл
ЗАДАЧА № 13 Найти неопределенный интеграл
ЗАДАЧА № 14 Найти неопределенный интеграл
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ Идея метода состоит в том, что подынтегральное выражение f(x)dx нужно представить в виде произведения U*dV, где U(x) и V(x) - дифференцируемые функции и воспользоваться формулой При этом вновь полученный интеграл ЗАДАЧА № 15 Найти неопределенный интеграл
ЗАДАЧА № 16 Найти неопределенный интеграл
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 5055; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 , если он существует. Частная производная
, если он существует. Частная производная  есть обычная производная от функции f(x,y), рассматриваемой как функция только от переменной х при фиксированном у.
есть обычная производная от функции f(x,y), рассматриваемой как функция только от переменной х при фиксированном у.
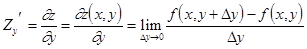 .
.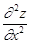 . Таким образом,
. Таким образом, 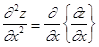 .
. .
.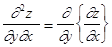 .
.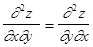 .
.  ,
, а потом воспользоваться приведенной выше формулой.
а потом воспользоваться приведенной выше формулой.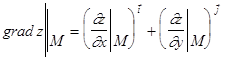 .
. функции z = f(x,y):
функции z = f(x,y):
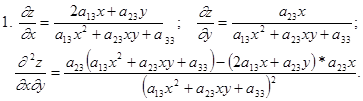
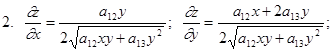
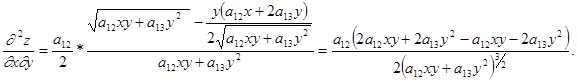
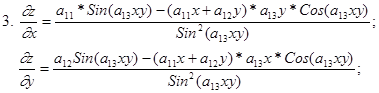


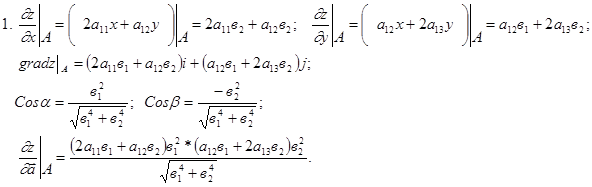

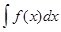 называется функция F(x) + C, производная которой равна подынтегральной функции f(x), т.е.
называется функция F(x) + C, производная которой равна подынтегральной функции f(x), т.е.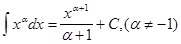

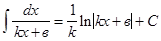
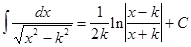

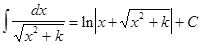
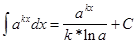
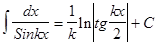
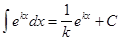

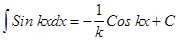

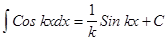

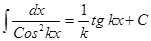
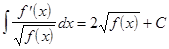


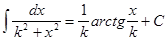
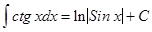
 , т.е. знаки d и ò, стоящие перед некоторой функцией, друг друга уничтожают. Так
, т.е. знаки d и ò, стоящие перед некоторой функцией, друг друга уничтожают. Так 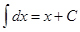 .
.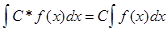 , т.е. постоянный множитель можно выносить за знаки интеграла.
, т.е. постоянный множитель можно выносить за знаки интеграла. , т.е. неопределенный интеграл от суммы некоторых функций равен сумме интегралов от этих функций.
, т.е. неопределенный интеграл от суммы некоторых функций равен сумме интегралов от этих функций. .
.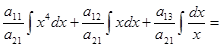
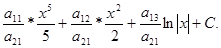
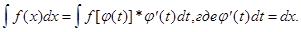 Получаемый интеграл должен быть значительно проще данного. В противном случае следует искать другую форму введения новой переменной. Часто переменную t вводят так: t = j(x), а dt = j¢(x)dx. Это удобно, если данное подынтегральное выражение содержит дифференциал j¢(x)dx.
Получаемый интеграл должен быть значительно проще данного. В противном случае следует искать другую форму введения новой переменной. Часто переменную t вводят так: t = j(x), а dt = j¢(x)dx. Это удобно, если данное подынтегральное выражение содержит дифференциал j¢(x)dx. .
.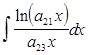 =
= 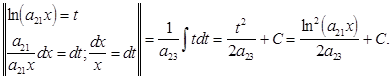
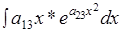 .
. .
.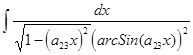 .
.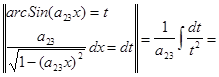

 .
.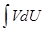 должен быть проще данного.
должен быть проще данного. .
.

 .
.