
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции при стремлении аргумента к бесконечностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функции. Предел функции 1. Понятие функции. Способы задания функции
Определение. Пусть
Читается: « Определение. Графиком функции Основными способами задания функции являются: аналитический (т.е. с помощью формулы, выражающей При аналитическом задании функции обычно считается, что область ее определения совпадает с областью допустимых значений (ОДЗ) аргумента
является множество Примером словесного задания функции является функция Дирихле: Заметим, что числовая последовательность - это функция с областью определения Основные свойства функций Функция
Функция
для любого Наименьшее из таких чисел называется периодом функции Например, функции Функция
Функция возрастающая (убывающая) на множестве А называется монотонной на этом множестве. Пусть Функция
Из этого определения следует, что график обратной функции Например, функций Пусть
Окрестностью точки Пусть
(от лат. maximum - наибольшее, minimum - наименьшее). Точки максимума и минимума функции В точках экстремума функция Наибольшим (наименьшим) значением функции
Предел функции в точке
Пусть функция Определение. Число
верно неравенство
То же определение может быть записано в другом виде: Если Запись предела функции в точке: Определение. Если
Приведенное выше определение относится к случаю, когда функция Пределы
Основные теоремы о пределах
Теорема 1. Следующие теоремы справедливы при предположении, что функции Теорема 2. Теорема 3. Следствие. Теорема 4.
Теорема 5. Если Аналогично определяется знак предела при Теорема 6. Если Определение. Функция Теорема 7. Если функция
Доказательство. Пусть
Теорема доказана.
Непрерывность функции Числовые последовательности Пример.
Для последовательностей можно определить следующие операции: 1) Умножение последовательности на число 2) Сложение (вычитание) последовательностей: 3) Произведение последовательностей: 4) Частное последовательностей:
Определении 1) Если 2) Если 3) Если 4) Если Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными. Пример. Пример. Доказать, что последовательность Найдем Найдем знак разности:
Таким образом, Пример. Выяснить является возрастающей или убывающей последовательность
Найдём Заметим, что монотонные последовательности являютс ограниченными по крайней мере с одной стороны. Теорема. Монотонная ограниченная последовательность имеет конечный предел. Доказательство. Рассмотрим монотонную неубывающую последовательность
Эта последовательность ограничена сверху: Так как
Для остальных монотонных последовательностей доказательство аналогично. Теорема доказана. Число е
Рассмотрим последовательность
или
Покажем, что последовательность
Докажем теперь, что при любом n ее члены не превосходят трех:
Таким образом, последовательность
Число
Число
Производная сложной функции
Теорема. Пусть Доказательство. Имеем
Переходя к пределу в обеих частях при
(с учетом того, что если Тогда
Свойства дифференциала
Если
1)
2) 3)
4)
Формула Тейлора Теорема Тейлора. 1) Пусть функция 2) Пусть х- любое значение из этой окрестности, причём Тогда между точками х и а найдется такая точка
- это выражение называется формулой Тейлора, а выражение:
называется остаточным членом в форме Лагранжа. Доказательство. Представим функцию
Чем больше значение Представим этот многочлен с неопределенными пока коэффициентами:
Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке
Решение этой системы при
…………………….
Подставляя полученные значения
Как было замечено выше, многочлен не точно совпадает с функцией Тогда:
Теорема доказана. Иногда используется другая запись для остаточного члена
Тогда, если принять
где
Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.
Формула Маклорена
Формулой Маклорена называется формула Тейлора при
Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют. Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно. Другими словами, чем больше по модулю значение разности Кроме того, можно показать, что остаточный член
Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.
По формуле Тейлора
Применение формулы Тейлора для разложения функций в степенной ряд широко используется и имеет огромное значение при проведении различных математических расчетов. Непосредственное вычисление интегралов некоторых функций может быть сопряжено со значительными трудностями, а замена функции степенным рядом позволяет значительно упростить задачу. Нахождение значений тригонометрических, обратных тригонометрических, логарифмических функций также может быть сведено к нахождению значений соответствующих многочленов. Если при разложении в ряд взять достаточное количество слагаемых, то значение функции может быть найдено с любой наперед заданной точностью. Практически можно сказать, что для нахождения значения любой функции с разумной степенью точности (предполагается, что точность, превышающая 10 – 20 знаков после десятичной точки, необходима очень редко) достаточно 4-10 членов разложения в ряд. Применение принципа разложения в ряд позволяет производить вычисления на ЭВМ в режиме реального времени, что немаловажно при решении конкретных технических задач.
Функция
Находим:
……………………
Тогда: Пример. Найдем значение числа
Для 8 членов разложения: e = 2,71827876984127003. Для 10 членов разложения: e = 2,71828180114638451. Для 100 членов разложения: e = 2,71828182845904553.
На графике показаны значения числа е с точностью в зависимости от числа членов разложения в ряд Тейлора. Следовательно, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 6-7 – ю членами ряда.
Функция Получаем
…………………………………………
Следовательно
Функция
Для функции
Функция (
…………………………………………………..
Тогда:
Если в полученной формуле принять
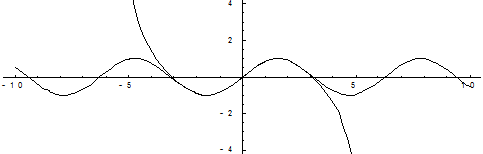
Получили формулу, известную как бином Ньютона. Пример. Применить полученную формулу для нахождения синуса любого угла с любой степенью точности. На приведенных ниже графиках представлено сравнение точного значения функции и значения разложения в ряд Тейлора при различном количестве членов разложения.
Два члена разложения
Четыре члена разложения
Шесть членов разложения
Десять членов разложения
Чтобы получить наиболее точное значение функции при наименьшем количестве членов разложения надо в формуле Тейлора в качестве параметра а выбрать такое число, которое достаточно близко к значению Для примера вычислим значение Предварительно переведем угол Применим разложение в ряд Тейлора, ограничившись тремя первыми членами разложения:
В четырехзначных таблицах Брадиса для синуса этого угла указано значение 0,3420.
На графике показано изменение значений разложения в ряд Тейлора в зависимости от количества членов разложения. Следоватеельно, если ограничиться тремя членами разложения, то достигается точность до 0,0002. Выше говорилось, что при Пример. Вычислить Для того чтобы представить заданный угол в радианах, воспользуемся соотношениями:
Если при разложении по формуле Тейлора ограничиться тремя первыми членами, получим: Сравнивая полученный результат с точным значением синуса этого угла,
видим, что даже при ограничении всего тремя членами разложения, точность составила 0,000002, что более чем достаточно для большинства практических технических задач. Функция Получаем: |

 - произвольное множество действительных чисел:
- произвольное множество действительных чисел:  . Говорят, что задана функция
. Говорят, что задана функция  с областью определения D, если каждому числу
с областью определения D, если каждому числу  из множества D поставлено в соответствие единственное действительное число
из множества D поставлено в соответствие единственное действительное число 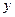 . Обозначение:
. Обозначение: .
. всех значений функции
всех значений функции 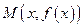 координатной плоскости, где
координатной плоскости, где  ), графический, табличный и словесный.
), графический, табличный и словесный. . Например, областью определения функции
. Например, областью определения функции
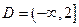 .
. , если
, если  если
если 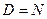 . В этом случае вместо
. В этом случае вместо  пишут просто
пишут просто  .
. ,
,  выполняется равенство:
выполняется равенство:
 .
. такое, что, если
такое, что, если  , то
, то
 являются периодическими с периодом
являются периодическими с периодом  , а функции
, а функции  - также периодические, но с периодом
- также периодические, но с периодом  .
. , если для любых
, если для любых  из А таких, что
из А таких, что  , выполняется неравенство
, выполняется неравенство
 .
. - множество ее значений.
- множество ее значений. с областью определения
с областью определения  .
. получается симметрированием графика данной функции
получается симметрированием графика данной функции  и
и  – взаимно-обратные.
– взаимно-обратные. - функция с областью определения
- функция с областью определения  . Обозначим через
. Обозначим через  множество тех значений аргумента
множество тех значений аргумента  . Тогда говорят, что на множестве
. Тогда говорят, что на множестве  .
. называется всякий открытый интервал с центром в точке
называется всякий открытый интервал с центром в точке  - окрестностью точки
- окрестностью точки  .
. называется точкой максимума (минимума), если существует
называется точкой максимума (минимума), если существует 

 (число
(число  ), что для всех
), что для всех 
 . Если функция
. Если функция  и ее график в каждой внутренней точке имеет единственную касательную, то наибольшее (наименьшее) значение функции
и ее график в каждой внутренней точке имеет единственную касательную, то наибольшее (наименьшее) значение функции  ,
,  и значений функции во всех точках максимума (минимума) этой функции.
и значений функции во всех точках максимума (минимума) этой функции. определена в некоторой окрестности точки
определена в некоторой окрестности точки  (т.е. в самой точке
(т.е. в самой точке  называется пределом функции
называется пределом функции  , если для любого
, если для любого  существует такое число
существует такое число  , что для всех
, что для всех 
 .
.
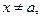 то верно неравенство
то верно неравенство  .
.
 при
при  , то
, то  - называется пределом функции
- называется пределом функции 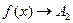 при
при 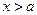 , то
, то  называется пределом функции
называется пределом функции 




 , где С = const.
, где С = const. имеют конечные пределы при
имеют конечные пределы при 
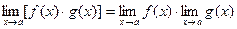

 при
при 
 в некоторой окрестности точки
в некоторой окрестности точки  .
. .
. в некоторой окрестности точки
в некоторой окрестности точки  , то
, то  .
. , что
, что  для всех точек
для всех точек  , тогда
, тогда или
или  , т.е.
, т.е.  где
где 
 или
или  .
. или
или 
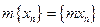 , т.е.
, т.е. 
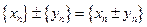 .
. .
. при
при  .
. для всех
для всех  , то последовательность называется возрастающей.
, то последовательность называется возрастающей. для всех
для всех  для всех
для всех  для всех
для всех  – убывающая и ограниченная;
– убывающая и ограниченная;  – возрастающая и неограниченная.
– возрастающая и неограниченная. монотонная и возрастающая.
монотонная и возрастающая.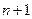 -й член последовательности
-й член последовательности 

 , т.к.
, т.к.  , то знаменатель положительный при любом
, то знаменатель положительный при любом  .
. . Определим разность
. Определим разность 
 , так как
, так как  , т.е.
, т.е. 

 , где
, где  такое, что
такое, что  , где
, где  - неубывающая последовательность, то при
- неубывающая последовательность, то при 
 ,
, . Отсюда
. Отсюда  или
или  или
или  , т.е.
, т.е.  .
. .Если последовательность
.Если последовательность 

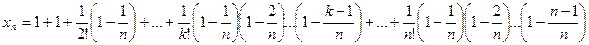
 и сравним его с выражением
и сравним его с выражением  Каждое слагаемое в выражении
Каждое слагаемое в выражении 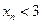 .
.
 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е. .
. является трпансцендентным числом и приблизительно равно
является трпансцендентным числом и приблизительно равно

 , причем область значений функции
, причем область значений функции  входит в область определения функции
входит в область определения функции 
 .
. получим:
получим: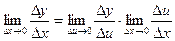 ,
, , т.к.
, т.к. 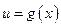 – непрерывная функция)
– непрерывная функция) . Теорема доказана.
. Теорема доказана. и
и  - функции, дифференцируемые в точке
- функции, дифференцируемые в точке 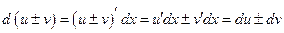



 включительно, (т.е. все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).
включительно, (т.е. все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).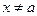 .
. , что справедлива формула:
, что справедлива формула:

 , значение которого в точке
, значение которого в точке  .
. .
.
 ,
, ,
, ,
, ,
, .
. в формулу (
в формулу ( ), получи:
), получи: .
. .
. .
. , то найдется такое число q из интервала
, то найдется такое число q из интервала  , что
, что 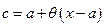 . Тогда можно записать:
. Тогда можно записать:
 ,
,  ,
,  , формулу Тейлора можно записать в виде:
, формулу Тейлора можно записать в виде:
 , получим:
, получим: .
. :
:

 тем более точное значение функции отличается от найденного по формуле Тейлора.
тем более точное значение функции отличается от найденного по формуле Тейлора. , т.е.
, т.е. .
.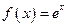 .
. ,
, ,
,  ,
, ,
,  ,
, .
. .
.


 ;
; ;
; 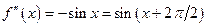 ;
;  ;
; ;
;  ;
; ;
;  ;
; ;
; 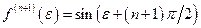 ;
;

 , применив аналогичные преобразования, получим:
, применив аналогичные преобразования, получим:

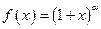
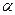 - действительное число)
- действительное число)

 .
. ;
; .
. , где
, где  то
то  , тогда
, тогда .
.


 .
. в радианы:
в радианы:  .
. .
.
 функция
функция  является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при
является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при  .
.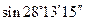 .
. ;
;  ;
;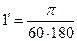 ;
;  ;
; ;
;  ;
; рад
рад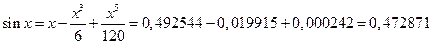 .
. = 0,472869017612759812,
= 0,472869017612759812,



