
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды Маклорена некоторых функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение Пусть Сумма (числового) ряда — это предел частичных сумм [править]Сходимость числовых рядов Свойство 1. Если ряд
сходится и его сумма равна S, то ряд
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится. Свойство 2. Если сходится ряд (1.1) и сходится ряд
а их суммы равны
причём сумма каждого равна соответственно [править]Необходимый признак сходимости ряда Ряд
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости. 3 Необходимый признак сходимости. Признак сходимости Даламбера
Радикальный признак Коши [править] Материал из Википедии — свободной энциклопедии У этого термина существуют и другие значения, см. Признак Коши. Радикальный признак Коши — признак сходимости числового ряда:
[править]Предельная форма Условие радикального признака равносильно следующему:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
[править]Доказательство 1. Пусть
Раскрыв модуль, получаем:
Поскольку 2. Пусть
Раскрыв модуль, получаем:
Поскольку 5 Знакочередующиеся ряды |
Знакочередующийся ряд
[править]
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2011; проверки требуют 6 правок.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
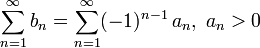
[править]Признак Лейбница
Основная статья: Теорема Лейбница о сходимости знакочередующихся рядов
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
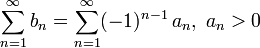 выполняются следующие условия:
1.
выполняются следующие условия:
1. 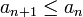 (монотонное невозрастание {an} по абсолютной величине)
2. (монотонное невозрастание {an} по абсолютной величине)
2.  .
Тогда этот ряд сходится. .
Тогда этот ряд сходится.
|
Замечания:

| Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения. |
Если, выполнены все условия, и ряд из модулей ( ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность
) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность  существенна.
существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
 . Ряд из модулей имеет вид
. Ряд из модулей имеет вид  — это гармонический ряд, который расходится.
— это гармонический ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
1. знакочередование выполнено 
2. 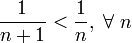
3.  .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
[править]Оценка остатка ряда Лейбница
Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена остатка ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
 .
.
6 абсолютная и условная сходимость знакопеременного ряда
Абсолютная и условная сходимость
Ряд 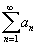 называется абсолютно сходящимся, если ряд называется абсолютно сходящимся, если ряд 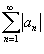 также сходится. Если ряд также сходится. Если ряд 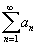 сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд 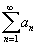 называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
|
| Пример 1 |
Исследовать на сходимость ряд  .
Решение.
Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем .
Решение.
Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем
 поскольку
поскольку  . Следовательно, данный ряд сходится. . Следовательно, данный ряд сходится.
|
| Пример 2 |
Исследовать на сходимость ряд  .
Решение.
Попробуем применить признак Лейбница: .
Решение.
Попробуем применить признак Лейбница:
 Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится
.
Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится
.
|
7 понятие степенного ряда.Ряд Тейлора,Маклорена
Степенной ряд
[править]
Материал из Википедии — свободной энциклопедии
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

в котором коэффициенты  берутся из некоторого кольца
берутся из некоторого кольца  .
.
| Содержание [убрать] · 1 Пространство степенных рядов · 2 Сходимость степенных рядов o 2.1 Признаки сходимости o 2.2 См.также · 3 Вариации и обобщения |
[править]Пространство степенных рядов
Сюда перенаправляется запрос «Формальный степенной ряд». На эту тему нужна отдельная статья.
Пространство степенных рядов с одной переменной и коэффициентами из  обозначается
обозначается  . Пространство
. Пространство  имеет структуру дифференциальной алгебры над кольцом
имеет структуру дифференциальной алгебры над кольцом  (коммутативной, целостной, с единицей, если таково же кольцо
(коммутативной, целостной, с единицей, если таково же кольцо  ). Оно часто используется в математике ввиду того, что в нём легко представимы и разрешимы формальные дифференциально-алгебраические и даже функциональные соотношения (см. метод производящих функций). При его использовании эти соотношения превращаются в алгебраические уравнения на коэффициенты рядов. Если они разрешаются, говорят о получении формального решения исходной задачи в виде формального степенного ряда.
). Оно часто используется в математике ввиду того, что в нём легко представимы и разрешимы формальные дифференциально-алгебраические и даже функциональные соотношения (см. метод производящих функций). При его использовании эти соотношения превращаются в алгебраические уравнения на коэффициенты рядов. Если они разрешаются, говорят о получении формального решения исходной задачи в виде формального степенного ряда.
В  определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть
определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть

Тогда:
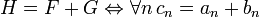

 (при этом необходимо, чтобы соблюдалось
(при этом необходимо, чтобы соблюдалось 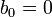 )
)

[править]Сходимость степенных рядов
Из формального степенного ряда с вещественными или комплексными коэффициентами путем приписывания формальной переменной  какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
[править]Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
§ Первая теорема Абеля: Пусть ряд  сходится в точке
сходится в точке  . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге  и равномерно по
и равномерно по  на любом компактном подмножествеэтого круга.
на любом компактном подмножествеэтого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при  , он расходится при всех
, он расходится при всех  , таких что
, таких что  . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга  (возможно, нулевой или бесконечный), что при
(возможно, нулевой или бесконечный), что при  ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по  на компактных подмножествах круга
на компактных подмножествах круга  ), а при
), а при 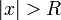 — расходится. Это значение
— расходится. Это значение  называется радиусом сходимости ряда, а круг
называется радиусом сходимости ряда, а круг  — кругом сходимости.
— кругом сходимости.
§ Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:

(По поводу определения верхнего предела 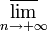 см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».)
Пусть 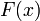 и
и  — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости  и
и  . Тогда
. Тогда



Если у ряда  свободный член нулевой, тогда
свободный член нулевой, тогда

Вопрос о сходимости ряда в точках границы  круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
§ Признак Д’Аламбера: Если при  и
и  выполнено неравенство
выполнено неравенство
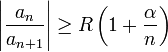
тогда степенной ряд  сходится во всех точках окружности
сходится во всех точках окружности  абсолютно и равномерно по
абсолютно и равномерно по  .
.
§ Признак Дирихле: Если все коэффициенты степенного ряда  положительны и последовательность
положительны и последовательность  монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности
монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности  , кроме, быть может, точки
, кроме, быть может, точки  .
.
§ Вторая теорема Абеля: Пусть степенной ряд сходится в точке  . Тогда он сходится равномерно по
. Тогда он сходится равномерно по  на отрезке, соединяющем точки 0 и
на отрезке, соединяющем точки 0 и  .
.
Сумма степенного ряда как функция комплексного параметра  является предметом изучения теории аналитических функций.
является предметом изучения теории аналитических функций.
Ряд Тейлора
[править]
Материал из Википедии — свободной энциклопедии
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а такжеНьютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
| Содержание [убрать] · 1 Определение · 2 Связанные определения · 3 Свойства o 3.1 Формула Тейлора o 3.2 Различные формы остаточного члена · 4 Ряды Маклорена некоторых функций · 5 Формула Тейлора для функции двух переменных · 6 См. также · 7 Литература |
[править]Определение
Пусть функция  бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд

называется рядом Тейлора функции  в точке
в точке  .
.
[править]Связанные определения
§ В случае, если  , этот ряд также называется рядом Макло́рена.
, этот ряд также называется рядом Макло́рена.
[править]Свойства
§ Если  есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке
есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке  области определения
области определения  сходится к
сходится к  в некоторой окрестности
в некоторой окрестности  .
.
§ Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности  . Например, Коши предложил такой пример:
. Например, Коши предложил такой пример:

У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке  равны нулю.
равны нулю.
[править]Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.
Теорема:
§ Пусть функция  имеет имеет  производную в некоторой окрестности точки производную в некоторой окрестности точки  , ,  § Пусть
§ Пусть  § Пусть
§ Пусть  — произвольное положительное число,
тогда: — произвольное положительное число,
тогда:  точка точка  при при  или или  при при  : :

|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
[править]Различные формы остаточного члена
В форме Лагранжа:

В форме Коши:

В интегральной форме:

Ослабим предположения:
§ Пусть функция  имеет
имеет  производную в некоторой окрестности точки
производную в некоторой окрестности точки 
§ И 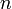 производную в самой точке
производную в самой точке  , тогда:
, тогда:
 — остаточный член в асимптотической форме (в форме Пеано, в локальной фо
— остаточный член в асимптотической форме (в форме Пеано, в локальной фо
Задача Коши
[править]
Материал из Википедии — свободной энциклопедии
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при 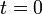 , а решение отыскивается при
, а решение отыскивается при 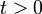 .
.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Основные вопросы, которые связаны с задачей Коши, таковы:
1. Существует ли (хотя бы локально) решение задачи Коши?
2. Если решение существует, то какова область его существования?
3. Является ли решение единственным?
4. Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят, что задача Коши имеет единственное решение, если она имеет решение  и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки
и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки  имеет поле направлений, совпадающее с полем направлений
имеет поле направлений, совпадающее с полем направлений 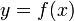 . Точка
. Точка 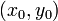 задаёт начальные условия.
задаёт начальные условия.
| Содержание [убрать] · 1 Различные постановки задачи Коши · 2 Теоремы о разрешимости задачи Коши для ОДУ · 3 См. также · 4 Литература |
[править]Различные постановки задачи Коши
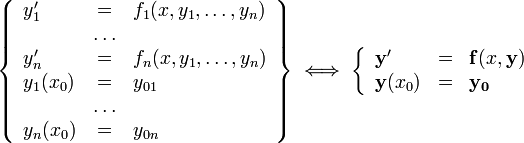
§ ОДУ первого порядка, разрешённое относительно производной

§ Система 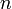 ОДУ первого порядка, разрешённая относительно производных (нормальная система
ОДУ первого порядка, разрешённая относительно производных (нормальная система 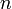 -го порядка)
-го порядка)
§ ОДУ 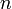 -го порядка, разрешённое относительно старшей производной
-го порядка, разрешённое относительно старшей производной
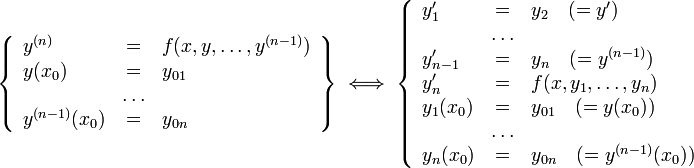
Тандартная модель
Комплексное число  можно определить как упорядоченную пару вещественных чисел
можно определить как упорядоченную пару вещественных чисел  . Введём операции сложения и умножения таких пар следующим образом:
. Введём операции сложения и умножения таких пар следующим образом:
§ 
§ 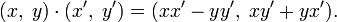
Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида  , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой
, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой  единица —
единица —  а мнимая единица —
а мнимая единица —  На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен
На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен  , то есть
, то есть 
Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.
Определение
Пусть  — числовой ряд. Число
— числовой ряд. Число 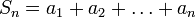 называется
называется 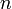 -ой частичной суммой ряда
-ой частичной суммой ряда  .
.
Сумма (числового) ряда — это предел частичных сумм  , если он существует и конечен. Таким образом, если существует число
, если он существует и конечен. Таким образом, если существует число  , то в этом случае пишут
, то в этом случае пишут 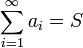 . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.
. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.
[править]Сходимость числовых рядов
Свойство 1. Если ряд
 (1.1)
(1.1)
сходится и его сумма равна S, то ряд
 (1.2)
(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
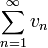 ,
,
а их суммы равны  и
и  соответственно, то сходятся и ряды
соответственно, то сходятся и ряды
 ,
,
причём сумма каждого равна соответственно  .
.
[править]Необходимый признак сходимости ряда
Ряд  может сходиться лишь в том случае, когда член
может сходиться лишь в том случае, когда член 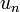 (общий член ряда) стремится к нулю:
(общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
3 Необходимый признак сходимости. Признак сходимости Даламбера
Определение: Пусть задана бесконечная последовательность чисел (действительных или комплексных)
 Числовым рядом называется выражение вида:
Числовым рядом называется выражение вида:
 .
Сокращенно ряд обозначают следующим образом: .
Сокращенно ряд обозначают следующим образом:  . При этом числа . При этом числа  называются членами ряда, называются членами ряда,  - общим членом ряда.
Необходимый признак сходимости ряда: Если ряд - общим членом ряда.
Необходимый признак сходимости ряда: Если ряд  сходиться, то общий член ряда сходиться, то общий член ряда  стремиться к нулю при стремиться к нулю при  , т.е. , т.е.
 .
Т.о. если .
Т.о. если  , то ряд , то ряд  расходится. Признак Д’Аламбера
[править]
Материал из Википедии — свободной энциклопедии
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда расходится. Признак Д’Аламбера
[править]
Материал из Википедии — свободной энциклопедии
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
 существует такое число
существует такое число 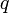 , ,  , что начиная с некоторого номера выполняется неравенство , что начиная с некоторого номера выполняется неравенство
 то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
 то ряд расходится.
[править]Признак сходимости д’Аламбера в предельной форме
Если существует предел
то ряд расходится.
[править]Признак сходимости д’Аламбера в предельной форме
Если существует предел
 то рассматриваемый ряд абсолютно сходится если
то рассматриваемый ряд абсолютно сходится если  , а если , а если  — расходится.
Замечание. Если — расходится.
Замечание. Если  , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
4 Признак сравнения. Радикальный признак Коши
Признак сравнения
[править]
Материал из Википедии — свободной энциклопедии
Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов. , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
4 Признак сравнения. Радикальный признак Коши
Признак сравнения
[править]
Материал из Википедии — свободной энциклопедии
Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.
[править]Формулировка
п·о·р Доказательство [показать] [править]Признак сравнения отношений Также признак сравнения можно сформулировать в более удобной форме — в виде отношений. [править]Формулировка
п·о·р Доказательство [показать] [править]Предельный признак сравнения Поскольку достоверно установить справедливость этого неравенства при любых n — довольно сложная задача, то на практике признак сравнения обычно используется в предельной форме. [править]Формулировка
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.100 (0.011 с.) |

 .
Тогда, если, начиная с некоторого места (
.
Тогда, если, начиная с некоторого места ( ,
то из сходимости ряда
,
то из сходимости ряда  ,
то из сходимости ряда
,
то из сходимости ряда 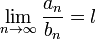 ,
то при
,
то при  из сходимости
из сходимости  из расходимости
из расходимости  ,
,  , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство 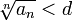 , то данный ряд сходится.
, то данный ряд сходится.

 , то
если
, то
если  ряд сходится,
если
ряд сходится,
если  ряд расходится,
если
ряд расходится,
если  вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.
 . Очевидно, что существует такое
. Очевидно, что существует такое  , что
, что  . Поскольку существует предел
. Поскольку существует предел  , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:



 сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 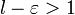 . Поскольку существует предел
. Поскольку существует предел  расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 


