
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциируемость сложной функцииСодержание книги
Поиск на нашем сайте Дифференциируемость сложной функции Пусть функции x(t), g(t) одной переменной t дифференциируемы в точке to и пусть х0=х(to), уо=у(tо). Если функция z=f(x(t)) дифференциируема в точке Мо(хо,уо), то сложная функция z=f(x(t),y(t)) определена в некоторой окрестности точки t0, имеет в этой точке производную и эта производная вычисляется по формуле:
№6. Полный дифференциал ф-ции неск. переменных Пусть дана функция z=f(x,y): D→R, DєR2, M0єD. Тогда для этой ф-ции справедливо: Δz=∂z/ ∂x(M0) Δx + ∂z/ ∂y(M0) Δy+α(Δx, Δy) Δx+ β(Δx, Δy) Δy Опр. Главная линейная часть приращения ф-ции (относительно Δx, Δy) наз. полным дифференциалом этой ф-ции в т. M0. Обозначается dz. dz=∂z/ ∂x│ M0* Δx+ ∂z/ ∂y│ M0* Δy, вместо Δx, Δy применяют dx и dy. Полный дифференциал можно использовать для приближенных вычислений значений функции. ∆z=f(M)-F(M0) ∆z≈dz f(x0+∆x, y0+∆y) ≈f(x0, y0)+ ∂z(x0, y0)/ ∂x * Δx +∂z(x0, y0)/ ∂y* Δy
№7-8. Экстремумы функций многих переменных Пусть функция z=f(x,y) определена в некоторой δ-окрестности точки М0(х0,у0).Тогда функция z=f(x,y)имеет в точке М0 максимум(минимум), если для всех точек этой окрестности выполняется неравенство f(x0,y0)>f(x,y) (f(x0,y0)<f(x,y)). Теорема. Необходимое условие экстремума. Пусть функция z=f(x,y) имеет экстремум в точке М0(х0,у0). Тогда если в этой точке существуют конечные частные производные первого порядка, то они равны нулю. Критические точки (подозрительные на экстремум) – те точки, в к-рых все частные производные первого порядка равны нулю. Теорема. Достаточные условия экстремума. Пусть ф-ция z=f(x,y) дифференцируема в точке М0(х0,у0), ∂f(x0,y0) ∂f(x0,y0) причем ∂x =0 и ∂y =0, и имеет в ней и в некоторой ее δ-окрестности частные производные второго порядка: ∂2z ∂2z ∂2z ∂x2=A, ∂x∂y= B, ∂y2=C. Тогда если определитель второго порядка │А В│ ∆=│В С│=АС-В2>0, то в точке М0(х0,у0) функция z=f(x,y) имеет экстремум, причем если A<0, - максимум, а если А>0, - минимум. В случае AC-B2=0 требуются дополнительные исследования. Для нахождения наибольшего и наименьшего значений функции двух переменных в заданной области в дополнение к заданным точкам экстремума находят ее значения на границе области.
№8 Достаточное условие экстремума функции двух переменных. Пусть функция z=f(x,y) дифференцируется в точке М0(x0,y0), причем (∂f(x0,y0)/∂x)=0 и (∂f(x0,y0)/∂х)=0, и имеет в ней и в некоторой ее δ-окрестности частные производные второго порядка: (∂^2z/∂x^2)=A, (∂^2z/∂x∂y)=B, ∂^2z/∂y^2=C. Тогда если определитель второго порядка ▲=│A B│ │B C│=AC-B^2>0, то в точке M0(x0, y0) функция z=f(x,y) имеет экстремум, причем если А< 0, - максимум, а если А> 0, - минимум. В случае АС-В^2 < 0 функция z = f(x,y) экстремума не имеет. В случае требуются дополнительные исследования.
Пример Найти экстремум функции z=2x^2+y^2-4x+8y-7 Находим: (∂z/∂x)=4x-4, (∂z/∂y)=2y+8. Критической точкой является точка с координатами 1, -4. Вычисляем величины А, В и С. A=(∂^2z/∂x^2)=4, B=(∂^2z/∂x∂y)=0, C=(∂^2y/∂y^2)=2
Составляем определитель и вычисляем его значение: ∆=│4 0│ │0 2│=δ>0. Так как ∆>0 и А >0,то (1, -4) – точка минимума и zmin = 2+16-4-32-7=-25
Для нахождения наибольшего и наименьшего значений функции двух переменных в заданной области(как и в случае одной переменной) в дополнение к заданным точкам экстремума находят ее значения на границе области. Так, если граница области задана уравн. y=φ(x), то находят наименьшее и наибольшее значения функции z=f(x,φ(x)).Затем из всех найденных функций выбирают наибольшее и наименьшее.
№9. Наибольшее и наименьшее значение непрерывной функции в замкнутой области. Z=f(x;y):D→R, D?R2 D-замкнутая область-область, содержащая все свои предельные точки. Z=f(x:y), f-дифференцируема в D. 1. Найти стационарные точки. 2. Найти наибольшее и наименьшее значения функции на граничной области. 3. Сравнить все значения и выбрать среди них наибольшее и наименьшее значение.
Геом. и экон. приложения опр. интеграла. S плоской фигуры. Объем тела вращения y=f(x) (f(x)≥0), то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми x=a и x=b и отрезком оси абсцисс a≤x≤b, определяется формулой
Объём тела вращения криволин. трапеции, ограниченной кривой y= f(x), осью Ох и двумя прямыми x=a и x=b, вокруг оси Ох
Объём тела, образов. вращением вокруг оси Oy фигуры, огранич. кривой x=g(y), осью Oy и двумя прямыми y=c и y=d, Длина дуги гладкой кривой y=f(x) между двумя точками с абсциссами x=a и x=b
Средняя производительность труда, средняя мощность и др. вычисляется по формуле
Дифф-е ур-я. Соотношение вида Задача Коши:
№29.Диф уравнения 1-го порядка с разделяющимися переменными и приводящиеся к ним. Уравнение вида y´=f(x)g(y)-уравнение с разделяющимися переменными, m1(x)n1(y)dx+m2(x)n2(y)dy=0 -уравнение с разделяющимися переменными в симметричной форме. Основной метод решения- разделение переменных, т.е. умножение левой и правой частей уравнения на такой множитель, чтобы после упрощения при dx стояла функция только от х,при dy- только от y.
Проинтегрируем. Общий интеграл уравнений запишется в виде:
При умножении можно потерять соответственно решение y=y0, где g(y0)=0, для первого уравнения, или x=x0, где m2(x0)=0, и y=y0, где n1(y0)=0, для второго. Эти случаи следует рассматривать отдельно. Найти yk, такие, что g(yk)=0, и проверить являются ли y=yk решениями уравнения и заключены ли они в общем интеграле при каком-то значении Сk;аналогично для второго уравнения. Уравнение вида y´=f(ax+by+c) приводится к уравнению с разделяющимися переменными. ax+by+c=z(x) z´=a+by´; z´=a-+bf(z); dz/dx=a+bf(z).
№30 Однородные диф. уравнения 1-ого порядка. dy/dx = f (y/x) – однородное уравнение 1-го порядка Функция n переменных z = f (x1, x2,…,xn) называется однородной функцией степени
если №31. Линейные дифференциальные уравнения первого порядка. Методы решения. Линейное диф уравнение перв порядка - ур первой степени относительно у и у', т.е. ур вида у'+P(x)y=Q(x) (если Q(x)≡0, то уравнение однородное, если не равно то неоднородное) -Решение однородного уравнения
Общее решение: -Реш неоднородного ур: 1 метод Бернулли. искомая функция представляется в виде произведения двух функций
можно одну из составляющих произведение функций выбрать так, что выражение возможно получить функцию u, проинтегрировав, полученное соотношение как однородное диф уравнение. Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение
Окончательно получаем формулу:
Вронскиан. Если решения у1(х), у2(х) уравнения (11.21) линейно независимы, то решение у(х)=С1у1(х)+С2у2(х), где С1,С2 – произвольные портоянные, является общим. Доказательство. Для доказательства следует лишь проверить то, что функция у=С1у1+С2у2 решает любую задачу Коши для начальных условий (х0? Х, у0,у’0). Пусть х? Х, у0,у’0 – произвольные числа. Для решения задачи Коши необходимо и достаточно, чтобы линейная система относительно С1 И С2 у1(х0)С1+у2(х)С2=у0, │ у’1(х0)С1+у’2(х0)С2=у0 │ (11.25) имела единственное решение для любых х0? Х, у0, у’0. Это условие эквивалентно тому, чтобы на Х
W’(x)=│y1(x) y2(x) │ │ y’1(x) y’2(x)│= y1(x) y’2(x)- y’1(x) y2(x) ≠ 0 (11.26) Покажем, что если определитель W(x) отличен от нуля в одной точке х0? Х, то он отличен от нуля на всем множестве Х. Определитель W(x) называется вронскианом или Определителем Вронского уравнения (11.21). Пусть в некоторой точке х0? Х W(x0) = W0≠0. Продифференцировав Ур.(11.26), получим: W’(x)= y’1(x) y’2(x)+ y1(x) y’’2(x)-y1’’(x)y2(x)-y’1(x)y’2(x)=-(B(x)/A(x))(y1(x)y’2(x)-y’1(x)y2(x))=-(B(x)/A(x))W(x), Т.е. вронскиан удолетворяет линейному однородному дифференциальному уравнению W’(x)+(B(x)/A(x))W(x)=0, A значаит, х W(x)=W0exp(-∫ (В(t)/A(t)dt)). х0 Поскольку на X A(x)≠0 и A(х), B(x) непрерывны, то х Exp(-∫ (В(t)/A(t)dt)) непрерывна на X и не обращается в х0 нуль, что и доказывает утверждение. Пусть у1(х), у2(х) – линейно независимые решения ур (11.21):
Очевидно, что ψ’(x)≠ 0 на Х, тогда в некоторой Точке х0? Х ψ’(x)≠ 0. Имеем
(у2(х)/у1(х))’=((у1(х)у’2(x)-y’1(x)y2(x)/y1^2(x))=(W(x)/y1^2(x))=ψ’(x).
Таким образом Отсюда следует однозначная разрешимость уравнения (11.25) и то,что функция (11.22) есть общее решение Ур (11.21). Два линейно независимых решения у=у1(х), у=у2(х) называют фундаментальной систеиой решений уравнения (11.21)
№33. Комплексные числа. Комплексным числом - всякая упорядоченная пара (a;b) действительных чисел. Х,Y=R z:(x,y)→(x+iy)
i2=-1 Арифметические операции 1.Сложение и вычитание Z1=x1+y1, z2=x2+y2 z1+z2=x1+x2+i(y1+-y2) 2.Умножение чисел z1 z2=(x1+iy1)(x2+iy2)=x1 x2+x1 y2+x2 y2-y1 y2 z1z2=x 1x2-y1 y2+i(x 1y2+x2 y1) 3. Деление z1/z2= (x1+iy1)(x2-iy2)/(x2+iy2)(x2-iy2)=((x1x2+y1y1)+i(x2y1-x1y2))/x 22+y 22= (x1x2+y1y2)/(x 22 +y 22) + i(x1y1-x2y2/x 22+y 2 2) z=x+iy Тригонометрическая форма записи комплексного числа.
Дифференциируемость сложной функции Пусть функции x(t), g(t) одной переменной t дифференциируемы в точке to и пусть х0=х(to), уо=у(tо). Если функция z=f(x(t)) дифференциируема в точке Мо(хо,уо), то сложная функция z=f(x(t),y(t)) определена в некоторой окрестности точки t0, имеет в этой точке производную и эта производная вычисляется по формуле:
№6. Полный дифференциал ф-ции неск. переменных Пусть дана функция z=f(x,y): D→R, DєR2, M0єD. Тогда для этой ф-ции справедливо: Δz=∂z/ ∂x(M0) Δx + ∂z/ ∂y(M0) Δy+α(Δx, Δy) Δx+ β(Δx, Δy) Δy Опр. Главная линейная часть приращения ф-ции (относительно Δx, Δy) наз. полным дифференциалом этой ф-ции в т. M0. Обозначается dz. dz=∂z/ ∂x│ M0* Δx+ ∂z/ ∂y│ M0* Δy, вместо Δx, Δy применяют dx и dy. Полный дифференциал можно использовать для приближенных вычислений значений функции. ∆z=f(M)-F(M0) ∆z≈dz f(x0+∆x, y0+∆y) ≈f(x0, y0)+ ∂z(x0, y0)/ ∂x * Δx +∂z(x0, y0)/ ∂y* Δy
№7-8. Экстремумы функций многих переменных Пусть функция z=f(x,y) определена в некоторой δ-окрестности точки М0(х0,у0).Тогда функция z=f(x,y)имеет в точке М0 максимум(минимум), если для всех точек этой окрестности выполняется неравенство f(x0,y0)>f(x,y) (f(x0,y0)<f(x,y)). Теорема. Необходимое условие экстремума. Пусть функция z=f(x,y) имеет экстремум в точке М0(х0,у0). Тогда если в этой точке существуют конечные частные производные первого порядка, то они равны нулю. Критические точки (подозрительные на экстремум) – те точки, в к-рых все частные производные первого порядка равны нулю. Теорема. Достаточные условия экстремума. Пусть ф-ция z=f(x,y) дифференцируема в точке М0(х0,у0), ∂f(x0,y0) ∂f(x0,y0) причем ∂x =0 и ∂y =0, и имеет в ней и в некоторой ее δ-окрестности частные производные второго порядка: ∂2z ∂2z ∂2z ∂x2=A, ∂x∂y= B, ∂y2=C. Тогда если определитель второго порядка │А В│ ∆=│В С│=АС-В2>0, то в точке М0(х0,у0) функция z=f(x,y) имеет экстремум, причем если A<0, - максимум, а если А>0, - минимум. В случае AC-B2=0 требуются дополнительные исследования. Для нахождения наибольшего и наименьшего значений функции двух переменных в заданной области в дополнение к заданным точкам экстремума находят ее значения на границе области.
№8 Достаточное условие экстремума функции двух переменных. Пусть функция z=f(x,y) дифференцируется в точке М0(x0,y0), причем (∂f(x0,y0)/∂x)=0 и (∂f(x0,y0)/∂х)=0, и имеет в ней и в некоторой ее δ-окрестности частные производные второго порядка: (∂^2z/∂x^2)=A, (∂^2z/∂x∂y)=B, ∂^2z/∂y^2=C. Тогда если определитель второго порядка ▲=│A B│ │B C│=AC-B^2>0, то в точке M0(x0, y0) функция z=f(x,y) имеет экстремум, причем если А< 0, - максимум, а если А> 0, - минимум. В случае АС-В^2 < 0 функция z = f(x,y) экстремума не имеет. В случае требуются дополнительные исследования.
Пример Найти экстремум функции z=2x^2+y^2-4x+8y-7 Находим: (∂z/∂x)=4x-4, (∂z/∂y)=2y+8. Критической точкой является точка с координатами 1, -4. Вычисляем величины А, В и С. A=(∂^2z/∂x^2)=4, B=(∂^2z/∂x∂y)=0, C=(∂^2y/∂y^2)=2
Составляем определитель и вычисляем его значение: ∆=│4 0│ │0 2│=δ>0. Так как ∆>0 и А >0,то (1, -4) – точка минимума и zmin = 2+16-4-32-7=-25
Для нахождения наибольшего и наименьшего значений функции двух переменных в заданной области(как и в случае одной переменной) в дополнение к заданным точкам экстремума находят ее значения на границе области. Так, если граница области задана уравн. y=φ(x), то находят наименьшее и наибольшее значения функции z=f(x,φ(x)).Затем из всех найденных функций выбирают наибольшее и наименьшее.
№9. Наибольшее и наименьшее значение непрерывной функции в замкнутой области. Z=f(x;y):D→R, D?R2 D-замкнутая область-область, содержащая все свои предельные точки. Z=f(x:y), f-дифференцируема в D. 1. Найти стационарные точки. 2. Найти наибольшее и наименьшее значения функции на граничной области. 3. Сравнить все значения и выбрать среди них наибольшее и наименьшее значение.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.01 с.) |


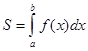

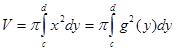




 - среднее значение функции.
- среднее значение функции. наз-ся обыкновенным ДУ n-го порядка, если в F явно входит
наз-ся обыкновенным ДУ n-го порядка, если в F явно входит  (старшая производная) и не входят производные
(старшая производная) и не входят производные 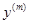 , где m>n. n определяет порядок ур-я. y’=f(x,y) – ур-е 1-го порядка. Если ф-я определена в
, где m>n. n определяет порядок ур-я. y’=f(x,y) – ур-е 1-го порядка. Если ф-я определена в  ,тоy=y(x) будет наз-ся решением ур-я
,тоy=y(x) будет наз-ся решением ур-я  (ур-е n-го порядка разрешенное относительно старшей производной) на
(ур-е n-го порядка разрешенное относительно старшей производной) на 
 нужно выделить реш-е, кот-е удовл. нач. условию (знак системы)
нужно выделить реш-е, кот-е удовл. нач. условию (знак системы) 


 ,
, 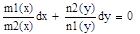
 ;
;  .
. , если формальная подстановка tx1 вместо x1, tx2 вместо х2,…, txn вместо xn, где t – любое допустимое число, после преобразований приведет к тождеству
, если формальная подстановка tx1 вместо x1, tx2 вместо х2,…, txn вместо xn, где t – любое допустимое число, после преобразований приведет к тождеству




 .
. - дифференцирование по частям. Подставляя в исходное уравнение, получаем:
- дифференцирование по частям. Подставляя в исходное уравнение, получаем:


 с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю. ;
; 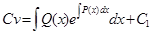 ;
;  ;
;
 =i (мнимая единица)
=i (мнимая единица) формула Эйлера
формула Эйлера


