Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная сложной функции нескольких переменных.Содержание книги
Поиск на нашем сайте Пусть z=f(x,y) – функция двух переменных. Если зафиксировать один из аргументов, например, взять y=y0, то получим функцию одной переменной z=f(x,y0). Частной производной функции z=f(x,y) в точке (x0,y0) по переменной x называется производная функции z=f(x,y0) в точке x=x0. Частная производная обозначается:
Дифференциалом функции z=f(x,y) называется выражение:
№11. Понятие об эмпирических формулах. Подбор параметров по способу наименьших квадратов. Выравнивание по прямой. Эмпирическая формула-это формула, полученная на основании экспериментальных данных. Она приближённо заменяет табличную так, чтобы её значения мало отличались от экспериментальных данных. Два этапа построения эмп. формулы: 1. подбор вида этой форм., зависящей от параметров, 2 определение по некоторому критерию её параметров. Попытаемся провести такую прямую, чтобы суммы квадратов отклонений были минимальны ∑Vi →min Этот же вопрос решим аналитически. Допустим, что значения точно удовлетворяют формуле y=ax+b, т.е. y1=ax1+b, …, yn=axn+b.Вычтем из каждого равенства предыдущее: y2-y1=a(x2-x1),…,yn-yn-1=a(xn-xn-1) y2-y1/ x2-x1=а=Δ1,…, yn-yn-1/ xn-xn-1=а=∆n-1. ∆-первая разделённая разность Теорема: прямая y=ax+b проходит через точки (хi,yi) тогда и только тогда, когда ∆1=∆2=…=∆n-1=a. Перейдём к нахождению параметров лин. формулы.В рез-те подстановки значений в y=ax+b должны появиться отклонения≠нулю. ax1+b- y1=v1,…, axn+b- yn=vn Найдем значения при кот. сумма квадр min z(a,b)=(ax1+b- y1)2+…+(axn+b- yn)2. Найдём наим значение этой функции. ∂z/∂a=2(ax1+b- y1) x1+...+2 (axn+b- yn) ∂z/∂b=2(ax1+b- y1)+…+ (axn+b- yn). Приравняем частные производные к 0 и составим сист.
Для решения достаточно, чтобы определитель из коэффициентов неизвестных ≠0.
В=∂2z/∂b2=2n C=∂2z/∂a∂b=2
Выражение АВ-С>0 и А>0, тогда функция имеет ед точку минимума, а это и будет наим значение.
№14. Основные свойства неопределенного интеграла: 1. d( 2. 3. 4. 5. Таблица основных интегралов: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. №15.Замена переменной в неопр.интеграле. Инт-е по частям. 1) Пусть функция т.е. 2) Если функции Док-во:
№16.Интегрирование рациональных функций. Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби P(x)/Q(x), причём степень числителя P(x) ниже степени знаменателя Q(x). Решается данная задача с помощью метода неопределённых коэффициентов. Если знаменатель правильной рациональной дроби раскладывается на множители:Q(x) = (x-a)a (x-b)b (x2+px+q)y…(x2+kx+r)z, где корни трёхчленов комплексные, то правильная дробь раскладывается на сумму простых дробей: P(x)/Q(x) = A1/ (x-a)+A2/ (x-a)2+…+Aa /(x-a)a+B1/(x-b)+B2/ (x-b)2+…+Bb/ (x-b)b+…+(M1x+N1)/ (x2+px+q)+ (M2x+N2)/ (x2+px+q)2+…+(Myx+Ny)/ (x2+px+q)y+…+(C1x+D1)/ (x2+kx+r)+(C2x+D2)+ …+(Сzx+Dz)/ (x2+kx+q)z, (a, b, …, z принадлежат N). Для вычисления неопределённых коэффициентов A1, A2,…, обе части равенства умножением его на знаменатель приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях x. Можно также определять эти коэффициенты, полагая в равенстве x равным числам, подобранным соответствующим образом. P(x) и Q(x) – многочлены
№18.Интегрирование выражений, содержащих тригонометрические функции. 1) Интегр. вида ∫sin ax cos bx dx, ∫ cos ax cos bx dx, ∫ sin ax sin bx dx, где a ≠ b, находятся с пом. формул: sin ax cos bx = ½ (sin(a-b)x + sin (a+b)x) cos ax cos bx = ½ (cos(a-b)x + cos(a + b)x) sin ax sin bx = ½ (cos(a-b)x - cos(a + b)x) 2) Интегр. вида I = ∫R(sin x, cos x)dx, где R – рациональная функция, приводящая к интегрированию рациональных функций с помощью подстановки tg(x/2)=t, x=2arctg t dx = 2 dt/(t2 +1) sin x= 2 tg (x/2)/ (1+tg2(x/2)) = 2t/(1+t2) cos x = (1-tg2(x/2))/ (1+tg2(x/2))= (1-t2)/ (1+t2) Т.к. I = ∫R(2t / (1+t2), то (1-t2) / (1+t2)) 2dt / (1+t2) Эта подстановка является универсальной для интегралов этого типа.
3) Интегралы вида I = ∫sinmx cosnx dx, где m и n – целые (не обязательно положительные) числа, если 1) n – целое, нечетное, >0, то заменяем sin x = t; 2) m - целое, нечетное, >0, то заменяем cos x = t; 3) m + n - четное, то заменяем tg x = t.
№ 20. Интегр. сумма и определение опред. интеграла. Пусть на отрезке [a;b] определена некот. ф-ция f(x). Зададим разбиение {
к-я наз. интегральной суммой или суммой Римана. Число А наз. пределом интегральных сумм Предел интегральных сумм обозначают Ф-я f(x) наз. интегрируемой на отрезке [a;b], если для данной ф-ции на указанном отрезке сущ-т предел А ее интегральных сумм σ. Число А наз. определенным интегралом от функции f(x) на отрезке [a;b] и обозначается №21. Геометрический смысл определенного интеграла. Если непрерывная кривая задана в прямоугольных координатах уравнением y=f(x) (f(x)≥0), то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми x=a и x=b и отрезком оси абсцисс a≤x≤b, опр-ся формулой
Объемы тел, образованных вращением криволинейной трапеции, ограниченной кривой y=f(x), осью OX и двумя прямыми x=a и x=b вокруг оси OX, выражается формулой
Под длиной дуги понимается предел, к которому стремится длина ломаной дуги, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена стремиться к 0. В этом случае кривая называется спрямляемой.
№22.Св-ва определенных интегралов: 1. ba∫c*f(x)dx=c* ab∫f(x)dx. 2. ba ∫(f 1 (x)+f 2 (x))dx= ba ∫f 1 (x)dx+ ba ∫f 2 (x)dx. 3. ba∫f(x)dx=- a b∫f(x)dx. 4. ba∫f(x)dx=ca∫f(x)dx+ bc∫f(x)dx. 5. ba∫f(x)dx=f(c)*(b-a). 6. f(x)>=0 на [a;b], то ba∫f(x)dx>=0. 7. f 1 (x)=<f 2 (x) при х?[a;b], ba ∫f 1 (x)=< ba ∫f 2 (x)dx. 8. m(b-a)=< ba ∫f(x)dx=<M(b-a) 9. - ba ∫│f(x)│=<dx ba ∫f(x)dx=< ba ∫│f(x)│dx.
№23 Терема о интегрируемости непрерывных функций и кусочно-непрерывных функций (без доказательства). 1) Если функция f(x) интегрируема на отрезке [a,b], то она ограничена на этом отрезке 2) Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке. 3) Если функция f(x) определена и монотонна на отрезке [a,b], то она интегрируема на этом отрезке 4) Если функция f(x) отграничена на отрезке [a,b] и непрерывна во всех точках этого отрезка, кроме конечного числа точек ck (k = 1,m) в которых функция имеет разрыв 1 рода, то эта функция интегрируема на отрезке [a,b]. 5) Если интегрируемую функцию изменить в конечном числе точек, то получим интегрируемую функцию с тем же интегралом.
№ 24. Формула Ньютона-Лейбница. Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
№25. Замена переменной и интегрирование по частям в определенном интеграле. Теорема. Если φ:[α,β]→[a,b] − непрерывно дифференцируемое отображение отрезка α ≤ t ≤ β в отрезок a≤x≤b, такое, что φ(α)=a и φ(β)=b, то при любой непрерывной на отрезке [a,b] функции f(x) функция f(φ(t))φ'(t) непрерывна на отрезке [a,b] и справедливо равенство
Если функции u(x) и v(x) имеют непрерывные производные на отрезке [a,b], то справедлива следующая формула интегрирования по частям:
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |





 Покажем, что найденные значения параметров из системы дают минимум функции. Найдём произв 2 порядка.
Покажем, что найденные значения параметров из системы дают минимум функции. Найдём произв 2 порядка. А=∂2z/∂a2=2
А=∂2z/∂a2=2 )=f(x)dx;
)=f(x)dx; =F(x)+C;
=F(x)+C; =
= 
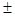
 ;
; =a
=a  (a
(a  0);
0); (
( )=f(x).
)=f(x). (a
(a 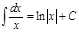 (x
(x  ;
; ;
; ;
; ;
;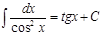 ;
; ;
; ;
; ;
;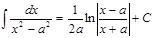 ;
;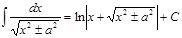 ;
; определена и дифференцируема на множестве
определена и дифференцируема на множестве  , и пусть
, и пусть  обозначает множество значений этой функции.Тогда если для функции
обозначает множество значений этой функции.Тогда если для функции  существует на множестве
существует на множестве  ,
, , то на множестве
, то на множестве  существует первообразная, равная
существует первообразная, равная 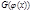 , т.е:
, т.е: 
 и
и  дифференцируемы на множестве
дифференцируемы на множестве 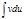 ,то на нем существует интеграл
,то на нем существует интеграл 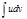 ,причем:
,причем:  -
- 


 }отрезка [a;b],
}отрезка [a;b], , такие, что
, такие, что  . Отрезки [
. Отрезки [  ] наз. частичными отрезками. Число
] наз. частичными отрезками. Число  , где
, где  , наз. диаметром разбиения. На каждом частичном отрезке выберем произвольные точки
, наз. диаметром разбиения. На каждом частичном отрезке выберем произвольные точки  . По данному разбиению {
. По данному разбиению {  } строим сумму
} строим сумму 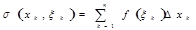 ,
, , если для любого ξ>0 существует такое δ= δ(ξ)>0, что для любого разбиения {
, если для любого ξ>0 существует такое δ= δ(ξ)>0, что для любого разбиения {  выполняется неравенство
выполняется неравенство 

 .
.


 ) = F(x)
) = F(x)  .
.