
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение функций и её основные свойства.Содержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» (МАИ)
Филиал «ВОСХОД»
Кафедра МиПОИС УТВЕРЖДАЮ Преподаватель ____________ Беловодская Л.А. «_____»__________ 2015 г.
Курсовая работа Тема: «Исследование функции и построение графиков» по дисциплине: «Математический анализ»
Студент Аникин И.А. гр. ДМ 1-40 подпись___________
«_____»__________ 2015 г.
Байконур 2015 г. Аннотация Данная курсовая работа состоит из теоретической и практической частей. Первая часть включает в себя теоретический материал на тему: «Исследование функции и построение графиков». Главной задачей курсовой работы является наиболее простое и наглядное изложение теоретического и практического материала по данной теме. Во второй части на рассмотрение предложено решение одиннадцати задач с приложенными к ним графиками и ответами.
Содержание: 1. Теоретическая часть 1.1. Определение функций и её основные свойства 1.2. Предел функции. Теорема о пределах 1.3. Непрерывная функция 1.4. Определение производной. Геометрический смысл производной. Скорость изменения функции 1.5. Построение графиков функций 1.5.1. Построение графиков функций с помощью элементарных преобразований 1.5.2. Построение графика функции с помощью свойств функции 1.6. Правила предельного перехода. Таблица производных 1.7. Вычисление приближенного значения с помощью дифференциала 1.8. Применение производной к исследованию функции 1.8.1. Необходимое и достаточное условие монотонности 1.8.2. Исследование функции на экстремумы 1.8.3. Наибольшее и наименьшее значение функции 1.8.4. Выпуклость и вогнутость функции 1.8.5. Точки перегиба функции 1.8.6. Асимптоты 1.9. Схема исследования функции и построение графика 2. Практическая часть
Теоретическая часть Определение функций и её основные свойства. Определение функции: Если каждому значению переменной величины х, принадлежащей некоторой совокупности (множеству Е), соответствует одно и только одно конечное значение величины y, то у называется функцией (однозначной) от х или зависимой переменной на множестве E; х называется аргументом или зависимой переменной. То обстоятельство, что y есть функция от x, то кратко выражают записью:
Основные свойства функции: 1. Область определения функции - это множество значений x, которые имеют соответствующие им значения функции. Обозначают На графике область определения - это промежутки на оси OX, над которыми (или под которыми) имеются части графика. 2. Область значений функции – это множество всех её значений Возрастание и убывание функции. Функция Функцию можно назвать возрастающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Функция Функцию можно назвать убывающей на промежутке, если у любых двух взятых из него чисел большему из них всегда соответствует меньшее значение функции.
4. Промежутки знакопостоянства. Промежутки, на которых значение функций имеют постоянный знак. Промежуток положительного знака – это множество значений переменной На графике – это части абцисс, у которых соответствующие кусочки графика выше оси Промежуток отрицательного знака – это множество тех значений переменной х, у которых соответствующее значение функции меньше нуля На графике – это промежутки оси абцисс, у которых соответствующие кусочки графика ниже оси найти, составив и решив Нули функции. Это значение переменной Без графика нули функции тоже можно найти, составив и решив По графику нули определяются как абциссы точек пересечения графика с осью Периодичность функций. Функция Если Если Т1>0 и T2>0 – периоды соответствующих функций
8. Точка экстремума функции (точка максимума, минимума) Точка Точка Определение по Гейне. Число А называется пределом функций Теорема о пределах. Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции
Теорема 3. (предел постоянной равен самой постоянной)
Доказательство. Возьмем произвольное Теорема 4. Функция не может иметь двух различных пределов в одной точке. Доказательство. Предположим противное. Пусть
По теореме о связи предела и бесконечно малой функции
Вычитая эти равенства,
Переходя к пределам, в общих частях равенства при Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при
Доказательство: Пусть
тогда, по теореме о связи предела бесконечно малой функции, где
Сложим алгебраически эти неравенства:
где По теореме о связи предела и бесконечно малой функции
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при Следствие: Постоянный множитель можно выносить за знак предела.
Теорема 7. Если функция
Непрерывная функция. Определение 1. Функция называется непрерывной в точке, если она определена в некоторой окрестности и предел приращения в этой точке тоже равен нулю.
Определение 2. Функция
Если Определение 3. Функция
Определение 4. Функция
Правила предельного перехода. Таблица производных. Правило 1. Если функция f непрерывна в точке Правило 2. Если функция f имеет производную в точке Эти правила следуют из определения непрерывности.
Правило 3. Пусть f(x) a) f(x) + б) f(x) × в) Для непрерывных функций f и А = f(x), B = И эти правила означают, что сумма, произведение и частное непрерывных в точке Таблица производных. Таблица 2
Правила дифференцирования.
u,f,v – функции; c = const Точки перегиба функции. Точкой перегиба называется такая точка линии, которая отделяет выпуклую дугу от вогнутой. В точке перегиба касательная пересекает линию, в окрестности этой точки линия лежит по обе стороны от касательной. Интервалу убывания первой производной соответствует участок выпуклости графика функции, а интервалу возрастания – участок вогнутости. Теорема (о точках перегиба): Если вторая производная Необходимый признак точки перегиба: Если Достаточный признак точки перегиба: Точка При Асимптоты. Определение. Асимптотой графика функции Виды асимптот: 1. Прямая Замечание: Прямая 2. Прямая Замечание: График функции может иметь только правую горизонтальную асимптоту или только левую. 3. Прямая Практическая часть
Задание 1.2. Построить график функции:
1. 2. 3. 4. График изображён в Приложении 1.
Задание 2.2. Выполнить исследование функции и построить её график:
1. Область определения функции:
2. Область значений функции:
3. Исследование на непрерывность:
Функция терпит разрыв в точке
4. Исследование на бесконечность:
5. Пересечение графика с осями координат:
Точки не существует, значит график не пересекает ось ОУ.
График изображён в Приложении 2. Задание 3.2. Построить график системы уравнений:
График изображён в Приложении 3.
Задание 4.2. С помощью дифференциала найти: 1) Приближённое значение функции 2) Точное значение функции 3) Абсолютную и относительную погрешность
1.Приближённое значение функции:
Ответ:
2. Точное значение функции:
Ответ: 3. Относительная и абсолютная погрешность:
Задание 5.2. Найти производные функций: 1.
2.
3.
4.
5.
Задание 6.2. Найти максимальное и минимальное значение функции на заданном промежутке:
ОДЗ:
Подставим полученное значение,а так же значения
Ответ: минимальное значение функции
Задание 7.2. Исследовать поведение функции в окрестности данной точки:
Для этого нужно найти производную высшего порядка Если
Ответ:
Задание 8.2. Найти асимптоты и построить график функции:
Проверим функцию на наличие наклонных и горизонтальных асимптот:
График не имеет наклонных асимптот
График изображён в Приложении 4. Задание 9.2. Провести полное исследование функции и построить её график:
1. Область определения функции:
2. Проверка функции на чётность/нечётность:
3. Исследование на периодичность: Функция дробно-рациональная, а значит не периодична.
4. Исследование на непрерывность:
5. Пересечения графика функции с осями координат:
6. Исследование на бесконечность:
Функция бесконечна.
7. Нахождение наклонных асимптот:
8. Исследование функции на монотонность:
9. Нахождение точек перегиба:
График изображён в Приложении 5. Задание 10.2. Провести полное исследование функции и построить её график:
1. Область определения функции:
2. Проверка функции на чётность/нечётность:
3. Исследование на периодичность: Функция дробно-рациональная, а значит не периодична.
4. Исследование на непрерывность:
5. Пересечения графика функции с осями координат:
6. Исследование на бесконечность:
Функция бесконечна.
7. Нахождение наклонных асимптот: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 и т.п.
и т.п.
 . Обозначают
. Обозначают  ). На графике область значений функций - это промежутки на оси
). На графике область значений функций - это промежутки на оси  , слева или справа от которых находятся части графика.
, слева или справа от которых находятся части графика. ) называется возрастающей, если для любых значений аргументов x1, x2 из неравенства
) называется возрастающей, если для любых значений аргументов x1, x2 из неравенства  следует неравенство
следует неравенство  .
. называется убывающей, если для любой пары значений аргументов x1, x2 из неравенства
называется убывающей, если для любой пары значений аргументов x1, x2 из неравенства  .
. у которых соответствующие значение функции больше нуль
у которых соответствующие значение функции больше нуль  .
. . Без графика их тоже можно найти, составив и решив неравенство
. Без графика их тоже можно найти, составив и решив неравенство  .
. .
. .
. , при которых
, при которых 
 .
.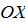 .
.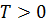 , если для любого
, если для любого  верно,
верно,  ).
). , то число
, то число  период функции
период функции 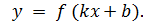
 , причем
, причем  =
=  где
где  , то любая комбинация этих функций
, то любая комбинация этих функций ).
).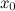 называется точкой максимума функции
называется точкой максимума функции  , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство:  .
. .
. при
при 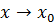 , если для любой последовательности значение аргумента
, если для любой последовательности значение аргумента  ;
; 
 …
…  , соответствует значению последовательности функции
, соответствует значению последовательности функции  сходится к
сходится к  .
.

 в окрестности некоторой точки не превосходят соответствующих значений функции
в окрестности некоторой точки не превосходят соответствующих значений функции  , то предел функции f(x) в этой точке не превосходит предела функции
, то предел функции f(x) в этой точке не превосходит предела функции 


 , докажем, что
, докажем, что  .
. . В качестве
. В качестве  можно взять любое положительное число. Тогда, при
можно взять любое положительное число. Тогда, при 

 и
и 
 - бесконечно малая при
- бесконечно малая при 

 - бесконечно малая при
- бесконечно малая при 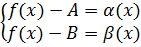
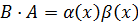
 , то есть
, то есть  . Получаем противоречие, доказывающее теорему.
. Получаем противоречие, доказывающее теорему.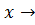


 ,
,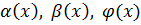 –бесконечно малы при
–бесконечно малы при 




 - бесконечно малые при
- бесконечно малые при 

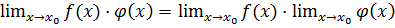

 и
и  , то их частное имеет предел при
, то их частное имеет предел при  ;
; 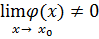

 равен значению функции в этой тоже
равен значению функции в этой тоже
 найдется
найдется  , что
, что выполняется, то выполняется |
выполняется, то выполняется |  .
. выполняется
выполняется  .
. , то
, то 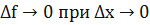 .
. , при
, при  .
. A,
A,  (x)
(x)  при х
при х  , тогда при
, тогда при  (
( A+B
A+B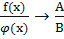 при B
при B  0
0 ).
).











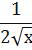


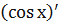


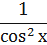













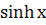









 всюду в интервале отрицательна, то дуга линии y = f(x), соответствующая этому интервалу, выпуклая. Если вторая производная
всюду в интервале отрицательна, то дуга линии y = f(x), соответствующая этому интервалу, выпуклая. Если вторая производная 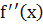 всюду в интервале положительна, то дуга линии y = f(x), соответствующая этому интервалу, вогнутая.
всюду в интервале положительна, то дуга линии y = f(x), соответствующая этому интервалу, вогнутая. , либо
, либо  не существует.
не существует. есть точка перегиба линии y = f(x), если
есть точка перегиба линии y = f(x), если  , а
, а  ;
; слева от нее лежит участок выпуклости, справа – участок вогнутости, а при
слева от нее лежит участок выпуклости, справа – участок вогнутости, а при  слева лежит участок вогнутости, а справа – выпуклости.
слева лежит участок вогнутости, а справа – выпуклости. называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки 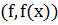 графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. называется вертикальной асимптотой графика функции y=f(x), если хотя бы одна из прямых значений
называется вертикальной асимптотой графика функции y=f(x), если хотя бы одна из прямых значений  или
или  равно
равно  или
или  .
. называется горизонтальной асимптотой графика функции y = f(x), если хотя бы одно из предельных значений
называется горизонтальной асимптотой графика функции y = f(x), если хотя бы одно из предельных значений  или
или  равно
равно  .
. называется наклонной асимптотой графика функции y = f(x), если
называется наклонной асимптотой графика функции y = f(x), если 


 – сдвиг влево на 1
– сдвиг влево на 1 – расширение графика в 2 раза
– расширение графика в 2 раза – сдвиг графика вниз на 2
– сдвиг графика вниз на 2




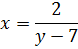


 .
. 

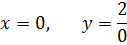



 –точка пересечения графика с осью ОХ.
–точка пересечения графика с осью ОХ.
 0;
0; ;
; ;
; ;
;









 Ответ:
Ответ: 






















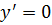



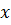 ,ограничивающие график функции,в функцию.
,ограничивающие график функции,в функцию. - минимальное значение функции
- минимальное значение функции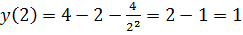 - максимальное значение функции
- максимальное значение функции
 ; максимальное значение функции
; максимальное значение функции  .
.
 .
.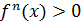 ,то
,то  ,то
,то 





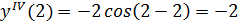
 - точка максимума.
- точка максимума.
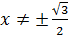


 – вертикальные асимптоты.
– вертикальные асимптоты.





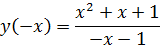
 – функция не является чётной
– функция не является чётной
 – функция не является нечётной
– функция не является нечётной .
.

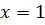 – точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит,
– точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит, 

 значит,график не пересекает ось ОX
значит,график не пересекает ось ОX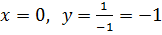 , график пересекает ось ОY в точке
, график пересекает ось ОY в точке  .
.



 – наклонная асимптота.
– наклонная асимптота.








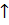








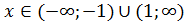




 – точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит,
– точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит, 
 значит,график не пересекает ось ОX
значит,график не пересекает ось ОX , график пересекает ось ОY в точке
, график пересекает ось ОY в точке  .
.




