
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение наклонной асимптоты.Содержание книги
Поиск на нашем сайте
Теорема (о условиях существования наклонной асимптоты): Если для функции y = f(x) существуют предел Замечания: 1. Горизонтальная асимптота является частым случаем наклонной при k = 0. 2. Если при нахождении горизонтальной асимптоты получается, что 3. Кривая y = f(x) может пересекать свою асимптоту, причём неоднократно. Схема исследования функции и построение графика. 1. Найти область определения функции. 2. Исследовать на чётность (нечётность). 3. Нахождение точек пересечения с осями координат и интервалы знакопостоянства. 4. Исследовать на периодичность. 5. Исследовать на непрерывность. Нахождение точек разрыва, установление их характера и нахождение вертикальных асимптот. 6. Исследовать поведение функции на бесконечность. Найдите предел 7. Найти наклонные асимптоты. 8. Найти участки монотонности и точке экстремума. 9. Найти интервалы выпуклости (вогнутости), точек перегиба. 10. Построить график функции. а) Построение асимптот. б) Построение точке пересечения с осями. в) Построение точек экстремума функции. г) Изучение поведения функции вблизи точек. д) Окончательное построение всего графика.
Практическая часть
Задание 1.2. Построить график функции:
1. 2. 3. 4. График изображён в Приложении 1.
Задание 2.2. Выполнить исследование функции и построить её график:
1. Область определения функции:
2. Область значений функции:
3. Исследование на непрерывность:
Функция терпит разрыв в точке
4. Исследование на бесконечность:
5. Пересечение графика с осями координат:
Точки не существует, значит график не пересекает ось ОУ.
График изображён в Приложении 2. Задание 3.2. Построить график системы уравнений:
График изображён в Приложении 3.
Задание 4.2. С помощью дифференциала найти:
1) Приближённое значение функции 2) Точное значение функции 3) Абсолютную и относительную погрешность
1.Приближённое значение функции:
Ответ:
2. Точное значение функции:
Ответ: 3. Относительная и абсолютная погрешность:
Задание 5.2. Найти производные функций: 1.
2.
3.
4.
5.
Задание 6.2. Найти максимальное и минимальное значение функции на заданном промежутке:
ОДЗ:
Подставим полученное значение,а так же значения
Ответ: минимальное значение функции
Задание 7.2. Исследовать поведение функции в окрестности данной точки:
Для этого нужно найти производную высшего порядка Если
Ответ:
Задание 8.2. Найти асимптоты и построить график функции:
Проверим функцию на наличие наклонных и горизонтальных асимптот:
График не имеет наклонных асимптот
График изображён в Приложении 4. Задание 9.2. Провести полное исследование функции и построить её график:
1. Область определения функции:
2. Проверка функции на чётность/нечётность:
3. Исследование на периодичность: Функция дробно-рациональная, а значит не периодична.
4. Исследование на непрерывность:
5. Пересечения графика функции с осями координат:
6. Исследование на бесконечность:
Функция бесконечна.
7. Нахождение наклонных асимптот:
8. Исследование функции на монотонность:
9. Нахождение точек перегиба:
График изображён в Приложении 5. Задание 10.2. Провести полное исследование функции и построить её график:
1. Область определения функции:
2. Проверка функции на чётность/нечётность:
3. Исследование на периодичность: Функция дробно-рациональная, а значит не периодична.
4. Исследование на непрерывность:
5. Пересечения графика функции с осями координат:
6. Исследование на бесконечность:
Функция бесконечна.
7. Нахождение наклонных асимптот:
Функция не имеет наклонных и горизонтальных асимптот. 8. Исследование функции на монотонность:
9. Нахождение точек перегиба:
График изображён в Приложении 6. Задание 11.2. Провести полное исследование функции и построить её график:
1. Область определения функции:
2. Проверка функции на чётность/нечётность:
3. Исследование на периодичность: Функция рациональная, а значит не периодична.
4. Исследование на непрерывность:
5. Пересечения графика функции с осями координат:
(1)
6. Исследование на бесконечность:
Функция бесконечна.
7. Нахождение наклонных асимптот:
8. Исследование функции на монотонность:
9. Нахождение точек перегиба:
График изображён в Приложении 7.
Заключение В данной работе были рассмотрены следующие теоретические вопросы: -Определение функций и её основные свойства; -Предел функции. Теорема о пределах; -Непрерывная функция; -Определение производной. Геометрический смысл производной. Скорость изменения функции; -Построение графиков функций; -Правила предельного перехода. Таблица производных; -Вычисление приближенного значения с помощью дифференциала; -Применение производной к исследованию функции; -Схема исследования функции и построение графика. Практическая часть содержит выполнение одиннадцати заданий: -В первом задании был построен график с использованием элементарных преобразований; - Во втором задании был построен график путём исследования свойств функций; -В третьем задании был построен график, состоящий из системы функций; -В четвёртом задании с помощью дифференциала были найдены: -приблизительное значение функции; -полное значение функции;
-абсолютная и относительная погрешность; -В пятом задании были найдены производные заданных функций; -В шестом задании с помощью с производной были найдены максимальные и минимальные значения функции; -В седьмом задании с помощью производной n-ого порядка было исследовано поведение функции в окрестности заданной точки; -В восьмом задании были найдены асимптоты и построен график; -В девятом, десятом и одиннадцатом задании было проведено полное исследование функций и построены графики.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.42 (0.01 с.) |

 и
и  , то функция имеет начальную асимптоту y = kx+b при
, то функция имеет начальную асимптоту y = kx+b при 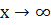 .
. , то функция может иметь наклонную асимптоту.
, то функция может иметь наклонную асимптоту.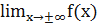 . Нахождение горизонтальных асимптот.
. Нахождение горизонтальных асимптот.

 – сдвиг влево на 1
– сдвиг влево на 1 – расширение графика в 2 раза
– расширение графика в 2 раза – сдвиг графика вниз на 2
– сдвиг графика вниз на 2




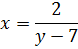


 .
. 

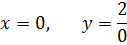



 –точка пересечения графика с осью ОХ.
–точка пересечения графика с осью ОХ.
 0;
0; ;
; ;
; ;
;









 Ответ:
Ответ: 






















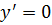



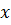 ,ограничивающие график функции,в функцию.
,ограничивающие график функции,в функцию. - минимальное значение функции
- минимальное значение функции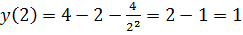 - максимальное значение функции
- максимальное значение функции
 ; максимальное значение функции
; максимальное значение функции  .
.
 .
.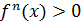 ,то
,то  ,то
,то 





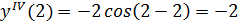
 - точка максимума.
- точка максимума.
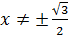


 – вертикальные асимптоты.
– вертикальные асимптоты.





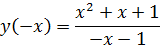
 – функция не является чётной
– функция не является чётной
 – функция не является нечётной
– функция не является нечётной .
.

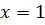 – точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит,
– точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит, 

 значит,график не пересекает ось ОX
значит,график не пересекает ось ОX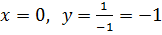 , график пересекает ось ОY в точке
, график пересекает ось ОY в точке  .
.



 – наклонная асимптота.
– наклонная асимптота.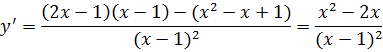








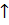








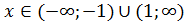




 – точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит,
– точка разрыва второго рода, так как пределы слева и справа равны бесконечности, значит, 
 значит,график не пересекает ось ОX
значит,график не пересекает ось ОX , график пересекает ось ОY в точке
, график пересекает ось ОY в точке  .
.




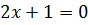




 – точка минимума
– точка минимума



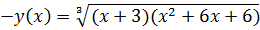
 значит, функция непрерывна на всей числовой прямой.
значит, функция непрерывна на всей числовой прямой.




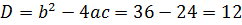
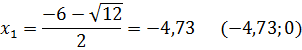

 , график пересекает ось ОY в точке
, график пересекает ось ОY в точке  .
.







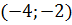

 – точка минимума
– точка минимума – точка максимума
– точка максимума




