
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое и достаточное условие монотонности.Содержание книги
Поиск на нашем сайте
Монотонная функция – это функция, меняющаяся в одном и том же направлении. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Говоря иначе, если при возрастании значения x значение y тоже возрастает, то это возрастающая функция. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Говоря иначе, если при возрастании значения x значение y убывает, то это убывающая функция. Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке. Функция постоянна (немонотонна), если она не убывает и не возрастает. Теорема (необходимый признак монотонности): 1. Если дифференцируемая функция f(x) в некотором интервале возрастает, то ее производная на этом интервале неотрицательна, т.е 2. Если дифференцируемая функция f(x) в некотором интервале убывает, то ее производная на этом интервале неположительна, 3. Если функция не изменяется, то ее производная равна нулю, т.е. Теорема (достаточный признак монотонности): Пусть f(x) непрерывна на интервале (a;b) и имеет производную во всех точках, тогда: 1. Если 2. Если 3. Если Исследование функции на экстремумы. Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. 1. Найдите область определения функции и интервалы, на которых функция непрерывна. 2. Найдите производную 3. Найдите критические точки, т.е. точки в которых производная функции равна нулю или не существует. 4. В каждом из интервалов на которые область определения разбивается критическими точками, определить знак производной и характер изменения функции. 5. Относительно каждой критической точки определить, является ли она точной максимума, минимума или не является точкой экстремума. Записать результат исследования функции промежутки монотонности и экстремума. Наибольшее и наименьшее значение функции. Схема нахождения наибольшего и наименьшего значений функции, непрерывной на отрезке. 1. Найти производную 2. Найти на данном отрезке критические точки. 3. Вычислить значение функции в критических точках и на концах отрезка. 4. Из вычисленных значений выбрать наименьшее и наибольшее. Выпуклость и вогнутость функции. Дуга называется выпуклой, если она пересекается с любой своей секущей не более, чем в двух точках. Линии, образуемые выпуклостью вверх, называются выпуклыми, а образуемые выпуклостью вниз - вогнутыми. Геометрически ясно, что выпуклая дуга лежит под любой своей касательной, а вогнутая дуга – над касательной. Точки перегиба функции. Точкой перегиба называется такая точка линии, которая отделяет выпуклую дугу от вогнутой. В точке перегиба касательная пересекает линию, в окрестности этой точки линия лежит по обе стороны от касательной. Интервалу убывания первой производной соответствует участок выпуклости графика функции, а интервалу возрастания – участок вогнутости. Теорема (о точках перегиба): Если вторая производная Необходимый признак точки перегиба: Если Достаточный признак точки перегиба: Точка При Асимптоты. Определение. Асимптотой графика функции Виды асимптот: 1. Прямая Замечание: Прямая 2. Прямая Замечание: График функции может иметь только правую горизонтальную асимптоту или только левую. 3. Прямая
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 9367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.007 с.) |

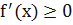 .
.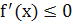 .
.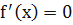 .
.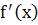 внутри (a;b) положительна, то f(x) возрастает.
внутри (a;b) положительна, то f(x) возрастает. всюду в интервале отрицательна, то дуга линии y = f(x), соответствующая этому интервалу, выпуклая. Если вторая производная
всюду в интервале отрицательна, то дуга линии y = f(x), соответствующая этому интервалу, выпуклая. Если вторая производная 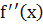 всюду в интервале положительна, то дуга линии y = f(x), соответствующая этому интервалу, вогнутая.
всюду в интервале положительна, то дуга линии y = f(x), соответствующая этому интервалу, вогнутая. – абсцисса точки перегиба, то либо
– абсцисса точки перегиба, то либо  , либо
, либо  не существует.
не существует. есть точка перегиба линии y = f(x), если
есть точка перегиба линии y = f(x), если  , а
, а  ;
; слева от нее лежит участок выпуклости, справа – участок вогнутости, а при
слева от нее лежит участок выпуклости, справа – участок вогнутости, а при  слева лежит участок вогнутости, а справа – выпуклости.
слева лежит участок вогнутости, а справа – выпуклости. называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки 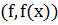 графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. называется вертикальной асимптотой графика функции y=f(x), если хотя бы одна из прямых значений
называется вертикальной асимптотой графика функции y=f(x), если хотя бы одна из прямых значений  или
или  равно
равно  или
или  .
. называется горизонтальной асимптотой графика функции y = f(x), если хотя бы одно из предельных значений
называется горизонтальной асимптотой графика функции y = f(x), если хотя бы одно из предельных значений  или
или  равно
равно  .
. называется наклонной асимптотой графика функции y = f(x), если
называется наклонной асимптотой графика функции y = f(x), если 



