
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возрастание и убывание функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функция Функцию можно назвать возрастающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Функция Функцию можно назвать убывающей на промежутке, если у любых двух взятых из него чисел большему из них всегда соответствует меньшее значение функции.
4. Промежутки знакопостоянства. Промежутки, на которых значение функций имеют постоянный знак. Промежуток положительного знака – это множество значений переменной На графике – это части абцисс, у которых соответствующие кусочки графика выше оси Промежуток отрицательного знака – это множество тех значений переменной х, у которых соответствующее значение функции меньше нуля На графике – это промежутки оси абцисс, у которых соответствующие кусочки графика ниже оси найти, составив и решив Нули функции. Это значение переменной Без графика нули функции тоже можно найти, составив и решив По графику нули определяются как абциссы точек пересечения графика с осью Четность и нечетность функции. Функция называется четной, если: Функция называется нечетной, если: Произведение или частное двух четных функций - есть функция четная. Произведение или частное двух нечетных функций – есть функция четная. Произведение или частное двух функций, одна из них четная, а другая нечетная – есть функция нечетная.
Периодичность функций. Функция Если Если Т1>0 и T2>0 – периоды соответствующих функций
8. Точка экстремума функции (точка максимума, минимума) Точка Точка Наименьшее и наибольшее значение функции. Число Число
Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число Если такого числа не существует, то функция – неограниченная.
Предел функции. Теорема о пределах. Определение предела по Коши. Число A называется пределом функции Определение по Гейне. Число А называется пределом функций Теорема о пределах. Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции
Теорема 3. (предел постоянной равен самой постоянной)
Доказательство. Возьмем произвольное Теорема 4. Функция не может иметь двух различных пределов в одной точке. Доказательство. Предположим противное. Пусть
По теореме о связи предела и бесконечно малой функции
Вычитая эти равенства,
Переходя к пределам, в общих частях равенства при Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при
Доказательство: Пусть
тогда, по теореме о связи предела бесконечно малой функции, где
Сложим алгебраически эти неравенства:
где По теореме о связи предела и бесконечно малой функции
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при Следствие: Постоянный множитель можно выносить за знак предела.
Теорема 7. Если функция
Непрерывная функция. Определение 1. Функция называется непрерывной в точке, если она определена в некоторой окрестности и предел приращения в этой точке тоже равен нулю.
Определение 2. Функция
Если Определение 3. Функция
Определение 4. Функция
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.140 (0.008 с.) |

 ) называется возрастающей, если для любых значений аргументов x1, x2 из неравенства
) называется возрастающей, если для любых значений аргументов x1, x2 из неравенства  следует неравенство
следует неравенство  .
. называется убывающей, если для любой пары значений аргументов x1, x2 из неравенства
называется убывающей, если для любой пары значений аргументов x1, x2 из неравенства  .
. у которых соответствующие значение функции больше нуль
у которых соответствующие значение функции больше нуль  .
. . Без графика их тоже можно найти, составив и решив неравенство
. Без графика их тоже можно найти, составив и решив неравенство  .
. .
. .
. , при которых
, при которых 
 .
.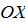 .
. нa противоположное
нa противоположное  значение функции не изменится, т.е.
значение функции не изменится, т.е.  для любого
для любого  из области определения функции.
из области определения функции. для любого
для любого 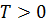 , если для любого
, если для любого  верно,
верно,  ).
). , то число
, то число  период функции
период функции 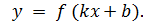
 , причем
, причем  =
=  где
где  , то любая комбинация этих функций
, то любая комбинация этих функций ).
).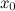 называется точкой максимума функции
называется точкой максимума функции  , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство:  .
. .
.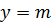 называется наименьшим значением функции на промежутке
называется наименьшим значением функции на промежутке  , если для любого значения аргумента
, если для любого значения аргумента 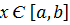 из этого промежутка верно неравенство
из этого промежутка верно неравенство называется наибольшим значением функции на промежутке
называется наибольшим значением функции на промежутке  .
. , что
, что  для всех значений
для всех значений 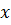 .
. ) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого
) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого  существует
существует  такое, что для всех x, удовлетворяющих условию |
такое, что для всех x, удовлетворяющих условию |  выполняется неравенство
выполняется неравенство 
 при
при 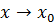 , если для любой последовательности значение аргумента
, если для любой последовательности значение аргумента  ;
; 
 …
…  , соответствует значению последовательности функции
, соответствует значению последовательности функции  сходится к
сходится к  .
.

 в окрестности некоторой точки не превосходят соответствующих значений функции
в окрестности некоторой точки не превосходят соответствующих значений функции  , то предел функции f(x) в этой точке не превосходит предела функции
, то предел функции f(x) в этой точке не превосходит предела функции 


 , докажем, что
, докажем, что  .
. . В качестве
. В качестве  можно взять любое положительное число. Тогда, при
можно взять любое положительное число. Тогда, при 

 и
и 
 - бесконечно малая при
- бесконечно малая при 

 - бесконечно малая при
- бесконечно малая при 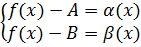
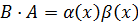
 , то есть
, то есть  . Получаем противоречие, доказывающее теорему.
. Получаем противоречие, доказывающее теорему.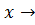


 ,
,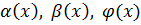 –бесконечно малы при
–бесконечно малы при 




 - бесконечно малые при
- бесконечно малые при 

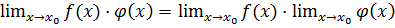

 и
и  , то их частное имеет предел при
, то их частное имеет предел при  ;
; 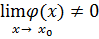

 равен значению функции в этой тоже
равен значению функции в этой тоже
 найдется
найдется  , что
, что выполняется, то выполняется |
выполняется, то выполняется |  .
. выполняется
выполняется  .
.


