
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервалы выпуклости и точки перегиба функции.Содержание книги
Поиск на нашем сайте Определение. Функция Теорема: Для того чтобы график дважды дифференцируемой на интервале (a; b) функции y = f (x) был выпуклым вверх (выпуклым вниз) на этом интервале, необходимо и достаточно, чтобы для любого f Точки, в которых f Пример 5. Найти промежутки выпуклости и точки перегиба графика функции Решение.
  – точка перегиба. – точка перегиба.
Пользуясь предыдущей теоремой, получаем, что на промежутке Асимптоты графика функции. Прямая
Прямая 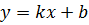 называется наклонной асимптотой графика функции называется наклонной асимптотой графика функции  . .
При Аналогично определяются асимптоты при Прямая Прямая Пример 6. Найти асимптоты графика функции Решение. Найдем
поэтому Функция не определена в точке
Таким образом, Замечание. Асимптота графика функции может пересекать сам график. Горизонтальные и наклонные асимптоты графика функции 1. Вычислить 2. Вычислить 3. Вычислить 4. Записать уравнение наклонной асимптоты: Пример 7. Исследовать функцию Решение. Обратимся к схеме исследования функции. 1. Найдем область определения функции. Так как функция задана дробным выражением, то знаменатель этой дроби должен быть отличен от 0. То есть 2. Точка
3. Найдем точки пересечения графика функции с осью Оу, то есть при Найдем точки пересечения графика функции с осью Ох, то есть при 4. Найдем промежутки знакопостоянства функции
Получили что на промежутках 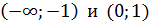 функция отрицательна, а на промежутках функция отрицательна, а на промежутках  – положительна. – положительна.
5. 1) Область определения функции – симметричное относительно начала координат множество. 2) Найдем
Получили что Из 1) и 2) следует, что функция нечетная. Функция не является периодической. 6. Для того чтобы найти промежутки монотонности функции, необходимо найти производную
и решить уравнение
При  производная не существует. Отметим эту точку на координатной прямой и расставим знаки производной на каждом полученном интервале. производная не существует. Отметим эту точку на координатной прямой и расставим знаки производной на каждом полученном интервале.
Значит, функция возрастает на каждом из промежутков 7. Экстремумов нет, так как производная не обращается в 0. 8. Чтобы определить промежутки выпуклости функции, нужно найти производную второго порядка от этой функции
и решить уравнение
Данное уравнение решений не имеет. Найдем точки, в которых производная второго порядка не существует. Это точка
Нанесем эту точку на координатную прямую и расставим знаки второй производной в каждом полученном интервале Значит, график функции выпуклый вниз на промежутке 9. Найдем асимптоты графика функции. Точка
Значит, Найдем так же
Исследуем функцию на наличие наклонных асимптот. Для этого найдем предел
Следовательно, прямая Найдем
Следовательно, прямая
 . .
10. Построим график функции.
Интеграл Неопределенный интеграл Определение. Функция Пример 1. Функция Определение. Множество всех первообразных Пример 2. а) б)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 выпукла вверх (выпукла вниз) в точке
выпукла вверх (выпукла вниз) в точке  , если существует интервал
, если существует интервал  такой, что для всех его точек х касательная к графику функции в точке
такой, что для всех его точек х касательная к графику функции в точке  лежит выше (ниже) графика.
лежит выше (ниже) графика. выполнялось неравенство
выполнялось неравенство (x)
(x)  (f
(f  ).
). или не существует, называют точками перегиба графика функции y = f (x).
или не существует, называют точками перегиба графика функции y = f (x). .
. .
. график функции выпуклый вверх, а на промежутке
график функции выпуклый вверх, а на промежутке  график функции выпуклый вниз.
график функции выпуклый вниз.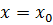 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы один из пределов
, если хотя бы один из пределов  равен
равен  .
.
 наклонная асимптота называется горизонтальной.
наклонная асимптота называется горизонтальной. и при
и при  .
. .
. .
. .
. ,
, – горизонтальная асимптота графика данной функции.
– горизонтальная асимптота графика данной функции. ,
, можно находить по следующему алгоритму.
можно находить по следующему алгоритму. . Если этот предел существует и равен некоторому числу с, то
. Если этот предел существует и равен некоторому числу с, то  – горизонтальная асимптота. Если предел не существует или равен бесконечности, то следует перейти ко второму пункту.
– горизонтальная асимптота. Если предел не существует или равен бесконечности, то следует перейти ко второму пункту.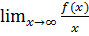 . Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел
. Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел  , то следует перейти к третьему шагу.
, то следует перейти к третьему шагу. . Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел
. Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел  , то следует перейти к четвертому шагу.
, то следует перейти к четвертому шагу. и построить ее график.
и построить ее график. 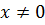 . Значит,
. Значит,  .
. :
: .
. .
. :
:  .
. .
. .
.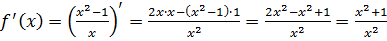
 .
. .
.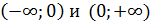 .
.
 .
. .
.
 .
.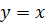 – наклонная асимптота графика функции при
– наклонная асимптота графика функции при 
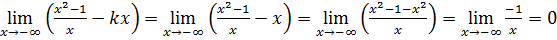 .
. называется перевообразной для функции
называется перевообразной для функции  , если для любого
, если для любого  .
. является первообразной для функции
является первообразной для функции  , так как
, так как  . Функция
. Функция 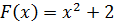 тоже является первообразной для функции
тоже является первообразной для функции  . Функция
. Функция  тоже является первообразной для функции
тоже является первообразной для функции  . Таким образом, множество всех первообразных для функции
. Таким образом, множество всех первообразных для функции  выглядит так:
выглядит так:  , где
, где  – некоторая постоянная.
– некоторая постоянная. для функции
для функции  называют неопределенным интегралом и обозначают
называют неопределенным интегралом и обозначают  .
.  называется подинтегральной функцией,
называется подинтегральной функцией,  – подинтегральным выражением,
– подинтегральным выражением, 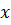 – переменной интегрирования.
– переменной интегрирования. .
. .
.


